本文大量参考了:
-
command_block 的博客:
位运算卷积(FWT) & 集合幂级数
FWT 概论
定义位运算卷积:
C
[
k
]
=
∑
i
⊕
j
=
k
A
[
i
]
B
[
j
]
C[k]=\sum\limits_{i\oplus j=k}A[i]B[j]
C
[
k
]
=
i
⊕
j
=
k
∑
A
[
i
]
B
[
j
]
,记作
C
=
A
∗
B
C=A*B
C
=
A
∗
B
,其中 $\oplus $ 为某一位运算。
设
A
,
B
A,B
A
,
B
下标的范围都是
[
0
,
n
−
1
]
[0,n-1]
[
0
,
n
−
1
]
且满足
n
n
n
是
2
2
2
的幂,那么卷出来
C
C
C
的下标范围也是
[
0
,
n
−
1
]
[0,n-1]
[
0
,
n
−
1
]
。
为了加速位运算卷积,我们尝试构造一个像 FFT 一样的算法,把卷积转化为直接点积。
设转化矩阵为
c
c
c
,即
F
W
T
(
A
)
=
c
A
FWT(A)=cA
F
W
T
(
A
)
=
c
A
,
F
W
T
(
A
)
[
i
]
=
∑
j
=
0
n
c
(
i
,
j
)
A
[
j
]
FWT(A)[i]=\sum\limits_{j=0}^nc(i,j)A[j]
F
W
T
(
A
)
[
i
]
=
j
=
0
∑
n
c
(
i
,
j
)
A
[
j
]
。使其满足:
F
W
T
(
A
)
[
i
]
⋅
F
W
T
(
B
)
[
i
]
=
F
W
T
(
C
)
[
i
]
(
∑
j
=
0
n
c
(
i
,
j
)
A
[
j
]
)
(
∑
j
=
0
n
c
(
i
,
j
)
B
[
j
]
)
=
(
∑
j
=
0
n
c
(
i
,
j
)
C
[
j
]
)
∑
j
=
0
n
∑
k
=
0
n
c
(
i
,
j
)
c
(
i
,
k
)
A
[
j
]
B
[
k
]
=
∑
j
=
0
n
c
(
i
,
j
)
∑
a
⊕
b
=
j
A
[
a
]
B
[
b
]
∑
j
=
0
n
∑
k
=
0
n
c
(
i
,
j
)
c
(
i
,
k
)
A
[
j
]
B
[
k
]
=
∑
j
=
0
n
∑
k
=
0
n
c
(
i
,
j
⊕
k
)
A
[
j
]
B
[
k
]
\begin{aligned}FWT(A)[i]\cdot FWT(B)[i]&=FWT(C)[i]\\\left(\sum_{j=0}^nc(i,j)A[j]\right)\left(\sum_{j=0}^nc(i,j)B[j]\right)&=\left(\sum_{j=0}^nc(i,j)C[j]\right)\\\sum_{j=0}^n\sum_{k=0}^nc(i,j)c(i,k)A[j]B[k]&=\sum_{j=0}^nc(i,j)\sum_{a\oplus b=j}A[a]B[b]\\\sum_{j=0}^n\sum_{k=0}^nc(i,j)c(i,k)A[j]B[k]&=\sum_{j=0}^n\sum_{k=0}^nc(i,j\oplus k)A[j]B[k]\end{aligned}
F
W
T
(
A
)
[
i
]
⋅
F
W
T
(
B
)
[
i
]
(
j
=
0
∑
n
c
(
i
,
j
)
A
[
j
]
)
(
j
=
0
∑
n
c
(
i
,
j
)
B
[
j
]
)
j
=
0
∑
n
k
=
0
∑
n
c
(
i
,
j
)
c
(
i
,
k
)
A
[
j
]
B
[
k
]
j
=
0
∑
n
k
=
0
∑
n
c
(
i
,
j
)
c
(
i
,
k
)
A
[
j
]
B
[
k
]
=
F
W
T
(
C
)
[
i
]
=
(
j
=
0
∑
n
c
(
i
,
j
)
C
[
j
]
)
=
j
=
0
∑
n
c
(
i
,
j
)
a
⊕
b
=
j
∑
A
[
a
]
B
[
b
]
=
j
=
0
∑
n
k
=
0
∑
n
c
(
i
,
j
⊕
k
)
A
[
j
]
B
[
k
]
只要满足
c
(
i
,
j
)
c
(
i
,
k
)
=
c
(
i
,
j
⊕
k
)
c(i,j)c(i,k)=c(i,j\oplus k)
c
(
i
,
j
)
c
(
i
,
k
)
=
c
(
i
,
j
⊕
k
)
即可让上式成立。
事实上我们也可以证明出必要性:由于这个式子需要对任意的
A
,
B
A,B
A
,
B
都成立(也就是说
A
[
1
]
,
⋯
,
A
[
n
]
,
B
[
1
]
,
⋯
,
B
[
n
]
A[1],\cdots,A[n],B[1],\cdots,B[n]
A
[
1
]
,
⋯
,
A
[
n
]
,
B
[
1
]
,
⋯
,
B
[
n
]
可以看成是
2
n
2n
2
n
个独立的变量),那么我们就必须要满足
c
(
i
,
j
)
c
(
i
,
k
)
=
c
(
i
,
j
⊕
k
)
c(i,j)c(i,k)=c(i,j\oplus k)
c
(
i
,
j
)
c
(
i
,
k
)
=
c
(
i
,
j
⊕
k
)
。
你可能会发现这个条件和
i
i
i
并没有关系,那你可能会想:能不能先找到一个数组
c
′
c’
c
′
满足
c
′
(
j
)
c
′
(
k
)
=
c
′
(
j
⊕
k
)
c'(j)c'(k)=c'(j\oplus k)
c
′
(
j
)
c
′
(
k
)
=
c
′
(
j
⊕
k
)
,然后让所有的
c
(
i
,
j
)
c(i,j)
c
(
i
,
j
)
都直接赋值为
c
′
(
j
)
c'(j)
c
′
(
j
)
就好了呢?
肯定是不行的,为了保证我们得到
F
W
T
(
C
)
=
c
×
C
FWT(C)=c\times C
F
W
T
(
C
)
=
c
×
C
后能得回
C
C
C
,我们还需要满足矩阵
c
c
c
有逆。而按刚刚的构造方法得到的矩阵
c
c
c
秩为
1
1
1
,没有逆。
现在的问题是我们要构造出
n
n
n
种数组
c
′
c’
c
′
使得它们都满足
c
′
(
j
)
c
′
(
k
)
=
c
′
(
j
⊕
k
)
c'(j)c'(k)=c'(j\oplus k)
c
′
(
j
)
c
′
(
k
)
=
c
′
(
j
⊕
k
)
,而且要求这
n
n
n
个数组拼起来得到的矩阵有逆。
一种巧妙的构造方式是:我们先构造出对于
n
=
2
n=2
n
=
2
时满足要求的矩阵,记为
c
1
c_1
c
1
。然后递推对于
n
=
2
k
(
k
>
1
)
n=2^k(k>1)
n
=
2
k
(
k
>
1
)
时满足的矩阵:
c
k
=
c
1
⊗
c
k
−
1
c_k=c_1\otimes c_{k-1}
c
k
=
c
1
⊗
c
k
−
1
。
其中
⊗
\otimes
⊗
为克罗内克积:对于大小为
n
×
n
n\times n
n
×
n
的矩阵
A
A
A
和大小为
m
×
m
m\times m
m
×
m
的矩阵
B
B
B
,它们的克罗内克积为:
A
⊗
B
=
[
A
1
,
1
B
⋯
A
1
,
n
B
⋮
⋱
⋮
A
n
,
1
B
⋯
A
n
,
n
B
]
A\otimes B=\begin{bmatrix}A_{1,1}B&\cdots&A_{1,n}B\\\vdots &\ddots &\vdots\\A_{n,1}B&\cdots&A_{n,n}B\end{bmatrix}
A
⊗
B
=
⎣
⎢
⎡
A
1
,
1
B
⋮
A
n
,
1
B
⋯
⋱
⋯
A
1
,
n
B
⋮
A
n
,
n
B
⎦
⎥
⎤
也就是说
c
k
c_k
c
k
为
c
1
c_1
c
1
的
k
k
k
级分形。设
n
=
2
m
n=2^m
n
=
2
m
,最后取
c
m
c_{m}
c
m
即为我们想要的
c
c
c
。
考虑这么做为什么是对的,我们需要证明两点:
c
(
i
,
j
)
c
(
i
,
k
)
=
c
(
i
,
j
⊕
k
)
c(i,j)c(i,k)=c(i,j\oplus k)
c
(
i
,
j
)
c
(
i
,
k
)
=
c
(
i
,
j
⊕
k
)
和矩阵
c
c
c
有逆。
-
定理 1
:
c(
i
,
j
)
c
(
i
,
k
)
=
c
(
i
,
j
⊕
k
)
c(i,j)c(i,k)=c(i,j\oplus k)
c
(
i
,
j
)
c
(
i
,
k
)
=
c
(
i
,
j
⊕
k
)
。
证明
:设
xt
x_t
x
t
表示
xx
x
在二进制下的第
tt
t
位,通过构造方式不难证明出
c(
i
,
j
)
=
∏
i
=
0
m
−
1
c
1
(
i
t
,
j
t
)
c(i,j)=\prod\limits_{i=0}^{m-1} c_1(i_t,j_t)
c
(
i
,
j
)
=
i
=
0
∏
m
−
1
c
1
(
i
t
,
j
t
)
。而矩阵
c1
c_1
c
1
是满足条件的。
c(
i
,
j
)
=
∏
i
=
0
m
−
1
c
1
(
i
t
,
j
t
)
c(i,j)=\prod\limits_{i=0}^{m-1} c_1(i_t,j_t)
c
(
i
,
j
)
=
i
=
0
∏
m
−
1
c
1
(
i
t
,
j
t
)
这条式子是非常好的记忆方法:即我们先找出对
n=
2
n=2
n
=
2
满足要求的矩阵,那么
c(
i
,
j
)
c(i,j)
c
(
i
,
j
)
就是
i,
j
i,j
i
,
j
拆位后各位的
cc
c
的乘积。
在证明矩阵
c
c
c
有逆之前,我们需要了解一个有关克罗内克积的引理。
-
引理 1
:对于大小为
n×
n
n\times n
n
×
n
的矩阵
AA
A
和大小为
m×
m
m\times m
m
×
m
的矩阵
BB
B
,设它们的克罗内克积为
C=
A
⊗
B
C=A\otimes B
C
=
A
⊗
B
,那么有:
∣C
∣
=
∣
A
∣
m
∣
B
∣
n
|C|=|A|^m|B|^n
∣
C
∣
=
∣
A
∣
m
∣
B
∣
n
证明
:考虑使用高斯消元法来求解行列式,那么
∣A
∣
|A|
∣
A
∣
的含义就是:
(−
1
)
μ
(
A
)
D
(
A
)
(-1)^{\mu(A)}D(A)
(
−
1
)
μ
(
A
)
D
(
A
)
,其中
D(
A
)
D(A)
D
(
A
)
表示将
AA
A
消为上三角矩阵后对角线上元素的乘积,
μ(
A
)
\mu(A)
μ
(
A
)
表示消元过程中使用操作”交换两行“的次数的奇偶性。现在考虑对
CC
C
进行高斯消元,我们可以每
mm
m
行一组按对
BB
B
消元的方式消元,共
nn
n
组,得到:(其中
B′
B’
B
′
为将矩阵
BB
B
消元后得到的上三角矩阵)
∣C
∣
=
(
−
1
)
n
⋅
μ
(
B
)
∣
[
A
1
,
1
B
′
⋯
A
1
,
n
B
′
⋮
⋱
⋮
A
n
,
1
B
′
⋯
A
n
,
n
B
′
]
∣
|C|=(-1)^{n\cdot \mu(B)}\left|\begin{bmatrix}A_{1,1}B’&\cdots&A_{1,n}B’\\\vdots &\ddots &\vdots\\A_{n,1}B’&\cdots&A_{n,n}B’\end{bmatrix}\right|
∣
C
∣
=
(
−
1
)
n
⋅
μ
(
B
)
∣
∣
∣
∣
∣
∣
∣
⎣
⎢
⎡
A
1
,
1
B
′
⋮
A
n
,
1
B
′
⋯
⋱
⋯
A
1
,
n
B
′
⋮
A
n
,
n
B
′
⎦
⎥
⎤
∣
∣
∣
∣
∣
∣
∣
然后再把每
m×
m
m\times m
m
×
m
的矩阵看成一格,然后用对
AA
A
消元的方式对剩下的这个
n×
n
n\times n
n
×
n
格的矩阵消元,得到:(其中
A′
A’
A
′
为将矩阵
AA
A
消元后得到的上三角矩阵)
∣C
∣
=
(
−
1
)
n
⋅
μ
(
B
)
(
−
1
)
m
⋅
μ
(
A
)
∣
[
A
1
,
1
′
B
′
⋯
A
1
,
n
′
B
′
⋮
⋱
⋮
A
n
,
1
′
B
′
⋯
A
n
,
n
′
B
′
]
∣
|C|=(-1)^{n\cdot \mu(B)}(-1)^{m\cdot \mu(A)}\left|\begin{bmatrix}A’_{1,1}B’&\cdots&A’_{1,n}B’\\\vdots &\ddots &\vdots\\A’_{n,1}B’&\cdots&A’_{n,n}B’\end{bmatrix}\right|
∣
C
∣
=
(
−
1
)
n
⋅
μ
(
B
)
(
−
1
)
m
⋅
μ
(
A
)
∣
∣
∣
∣
∣
∣
∣
⎣
⎢
⎡
A
1
,
1
′
B
′
⋮
A
n
,
1
′
B
′
⋯
⋱
⋯
A
1
,
n
′
B
′
⋮
A
n
,
n
′
B
′
⎦
⎥
⎤
∣
∣
∣
∣
∣
∣
∣
最后得到的这个矩阵是一个上三角矩阵,它的对角线的乘积为
D(
A
)
m
D
(
B
)
n
D(A)^mD(B)^n
D
(
A
)
m
D
(
B
)
n
,于是:
∣C
∣
=
(
−
1
)
n
⋅
μ
(
B
)
×
(
−
1
)
m
⋅
μ
(
A
)
×
D
(
A
)
m
×
D
(
B
)
n
=
(
(
−
1
)
μ
(
A
)
D
(
A
)
)
m
(
(
−
1
)
μ
(
B
)
D
(
B
)
)
n
=
∣
A
∣
m
∣
B
∣
n
\begin{aligned}|C|&=(-1)^{n\cdot \mu(B)}\times (-1)^{m\cdot \mu(A)}\times D(A)^m\times D(B)^n\\&=\left((-1)^{\mu(A)}D(A)\right)^m\left((-1)^{\mu(B)}D(B)\right)^n\\&=|A|^m|B|^n\end{aligned}
∣
C
∣
=
(
−
1
)
n
⋅
μ
(
B
)
×
(
−
1
)
m
⋅
μ
(
A
)
×
D
(
A
)
m
×
D
(
B
)
n
=
(
(
−
1
)
μ
(
A
)
D
(
A
)
)
m
(
(
−
1
)
μ
(
B
)
D
(
B
)
)
n
=
∣
A
∣
m
∣
B
∣
n
-
定理 2
:矩阵
cc
c
有逆。
证明
:矩阵有逆等价于矩阵行列式不为
00
0
。初始时
c1
c_1
c
1
满足条件,即
c1
c_1
c
1
行列式不为
00
0
。根据引理1可以归纳证明对于任意
kk
k
都有
ck
c_k
c
k
行列式不为
00
0
。
至此,我们证明了我们所构造出来的
c
c
c
是满足条件的转化矩阵。
而用这种构造方式构造出的
c
c
c
的一个好处是它能用分治加速转化的过程。
假设我们现在要求
c
k
A
c_k A
c
k
A
,其中
A
A
A
的下标范围为
[
0
,
2
k
−
1
]
[0,2^k-1]
[
0
,
2
k
−
1
]
:
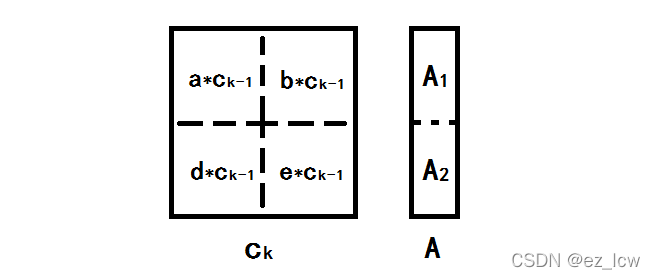
根据构造方式,我们可以将
c
k
c_k
c
k
分成四块,每块都是
c
k
−
1
c_{k-1}
c
k
−
1
的若干倍(具体来说,倍数分别为
c
1
c_1
c
1
中对应的的四个数)。那么我们也将
A
A
A
分成两半
A
1
,
A
2
A_1,A_2
A
1
,
A
2
,那么我们只需要求出
c
k
−
1
A
1
c_{k-1}A_1
c
k
−
1
A
1
和
c
k
−
1
A
2
c_{k-1}A_2
c
k
−
1
A
2
就能
O
(
2
k
)
O(2^k)
O
(
2
k
)
求出
c
k
A
c_kA
c
k
A
了。
于是就可以分治。具体来说,在第
k
k
k
轮时,我们将
0
∼
n
−
1
0\sim n-1
0
∼
n
−
1
每
2
k
2^k
2
k
分成一块,然后对于每一段
l
∼
r
(
r
−
l
+
1
=
2
k
)
l\sim r(r-l+1=2^k)
l
∼
r
(
r
−
l
+
1
=
2
k
)
,用
c
k
−
1
A
l
∼
m
i
d
c_{k-1}A_{l\sim mid}
c
k
−
1
A
l
∼
m
i
d
和
c
k
−
1
A
m
i
d
+
1
∼
r
c_{k-1}A_{mid+1\sim r}
c
k
−
1
A
m
i
d
+
1
∼
r
一起
O
(
2
k
)
O(2^k)
O
(
2
k
)
推导得到
c
k
A
l
∼
r
c_kA_{l\sim r}
c
k
A
l
∼
r
。
时间复杂度
O
(
n
log
n
)
O(n\log n)
O
(
n
lo
g
n
)
。
下面举几种位运算的例子。
Or 卷积
相当于要求两种线性无关的
c
c
c
使得它们都满足
c
(
j
)
c
(
k
)
=
c
(
j
∣
k
)
c(j)c(k)=c(j|k)
c
(
j
)
c
(
k
)
=
c
(
j
∣
k
)
。我们可以先求出所有的可能的
c
c
c
:(记
a
=
c
(
0
)
,
b
=
c
(
1
)
a=c(0),b=c(1)
a
=
c
(
0
)
,
b
=
c
(
1
)
)
{
a
⋅
a
=
a
a
⋅
b
=
b
b
⋅
b
=
b
\begin{cases}a\cdot a=a\\a\cdot b=b\\b\cdot b=b\end{cases}
⎩
⎪
⎨
⎪
⎧
a
⋅
a
=
a
a
⋅
b
=
b
b
⋅
b
=
b
得到
3
3
3
组解:
{
a
=
0
b
=
0
,
{
a
=
1
b
=
0
,
{
a
=
1
b
=
1
\begin{cases}a=0\\b=0\end{cases},\begin{cases}a=1\\b=0\end{cases},\begin{cases}a=1\\b=1\end{cases}
{
a
=
0
b
=
0
,
{
a
=
1
b
=
0
,
{
a
=
1
b
=
1
,唯一的方法是取后两组组成矩阵
c
1
=
[
1
0
1
1
]
c_1=\begin{bmatrix}1&0\\1&1\end{bmatrix}
c
1
=
[
1
1
0
1
]
。
And 卷积
类似,得到
c
1
=
[
0
1
1
1
]
c_1=\begin{bmatrix}0&1\\1&1\end{bmatrix}
c
1
=
[
0
1
1
1
]
。
Xor 卷积
类似,得到
c
1
=
[
1
1
1
−
1
]
c_1=\begin{bmatrix}1&1\\1&-1\end{bmatrix}
c
1
=
[
1
1
1
−
1
]
。
位值域扩展
注意到:or 卷积为模
2
2
2
意义下的高维 max 卷积,and 卷积为模
2
2
2
意义下的高维 min 卷积,xor 卷积为模
2
2
2
意义下的高维加法卷积。
事实上,我们也可以用类似的方法实现模
k
k
k
意义下的高维 max/min/加法 卷积。
设
n
=
k
b
n=k^b
n
=
k
b
。我们同样先构造出对于
n
=
k
n=k
n
=
k
时满足要求的
k
×
k
k\times k
k
×
k
矩阵
c
1
c_1
c
1
,然后
c
1
c_1
c
1
的
b
b
b
级分形即为我们要的转化矩阵
c
c
c
。同样,我们只需要证明
c
(
i
,
p
)
c
(
i
,
q
)
=
c
(
i
,
p
⊕
q
)
c(i,p)c(i,q)=c(i,p\oplus q)
c
(
i
,
p
)
c
(
i
,
q
)
=
c
(
i
,
p
⊕
q
)
且矩阵
c
c
c
有逆。
对于前者,我们类似地可以得到
c
(
i
,
j
)
=
∏
t
=
0
b
−
1
c
(
i
t
,
j
t
)
c(i,j)=\prod_{t=0}^{b-1} c(i_t,j_t)
c
(
i
,
j
)
=
∏
t
=
0
b
−
1
c
(
i
t
,
j
t
)
,其中
i
t
i_t
i
t
为
i
i
i
在
k
k
k
进制下第
t
t
t
位的值。那么就易证了。
而关于矩阵有逆的证明则没有任何变化,因为过程中我们只用到了克罗内克积的性质。
所以按照该方法构造出来的矩阵
c
c
c
仍然是满足要求的。
仍然是分治加速求
c
c
c
。在第
t
t
t
轮时,我们将序列每
k
t
k^t
k
t
分成一段,一段内用
O
(
k
⋅
k
t
)
O(k\cdot k^t)
O
(
k
⋅
k
t
)
的时间求出
c
t
A
l
∼
r
c_tA_{l\sim r}
c
t
A
l
∼
r
。于是每一轮的时间复杂度均为
O
(
k
n
)
O(kn)
O
(
k
n
)
,总时间复杂度
O
(
n
k
log
k
n
)
O(nk\log_kn)
O
(
n
k
lo
g
k
n
)
。
模
k
k
k
意义下的 max/min 卷积
先讲 max 卷积的情况。我们需要构造
k
k
k
组线性无关的
c
c
c
使得它们都满足
c
(
p
)
c
(
q
)
=
c
(
max
(
p
,
q
)
)
c(p)c(q)=c(\max(p,q))
c
(
p
)
c
(
q
)
=
c
(
max
(
p
,
q
)
)
。
取
p
=
q
p=q
p
=
q
我们首先可以确定
c
c
c
的值域为
{
0
,
1
}
\{0,1\}
{
0
,
1
}
。然后发现
c
(
p
)
c
(
q
)
=
c
(
max
(
p
,
q
)
)
c(p)c(q)=c(\max(p,q))
c
(
p
)
c
(
q
)
=
c
(
max
(
p
,
q
)
)
说明
c
c
c
数组肯定形如前一段是
1
1
1
后一段是
0
0
0
。那么除了全
0
0
0
之外恰好就有
k
k
k
组
c
c
c
。把它们按任意顺序拼成一个矩阵均可。
为了方便,一般采用形如
[
1
0
0
0
1
1
0
0
1
1
1
0
1
1
1
1
]
\scriptsize\begin{bmatrix}1&0&0&0\\1&1&0&0\\1&1&1&0\\1&1&1&1\end{bmatrix}
⎣
⎡
1
1
1
1
0
1
1
1
0
0
1
1
0
0
0
1
⎦
⎤
这种方式,其逆为
[
1
0
0
0
−
1
1
0
0
0
−
1
1
0
0
0
−
1
1
]
\scriptsize\begin{bmatrix}1&0&0&0\\-1&1&0&0\\0&-1&1&0\\0&0&-1&1\end{bmatrix}
⎣
⎡
1
−
1
0
0
0
1
−
1
0
0
0
1
−
1
0
0
0
1
⎦
⎤
。
发现其本质上就是前缀和及差分,所以单次求
c
t
A
l
∼
r
c_tA_{l\sim r}
c
t
A
l
∼
r
的时间可以从
O
(
k
⋅
k
t
)
O(k\cdot k^t)
O
(
k
⋅
k
t
)
优化到
O
(
k
t
)
O(k^t)
O
(
k
t
)
。总时间复杂度降为
O
(
n
log
k
n
)
O(n\log_kn)
O
(
n
lo
g
k
n
)
。
从更宏观的角度来说,这个过程就是在做一个高维前缀和(每一轮做了一位的前缀和)以及高维差分(每一轮做了一位的差分)。
min 卷积也是类似的,只不过
c
c
c
数组肯定形如前一段是
0
0
0
后一段是
1
1
1
罢了。
模
k
k
k
意义下的加法卷积
我们需要构造
k
k
k
组线性无关的
c
c
c
使得它们都满足
c
(
p
)
c
(
q
)
=
c
(
(
p
+
q
)
m
o
d
k
)
c(p)c(q)=c((p+q)\bmod k)
c
(
p
)
c
(
q
)
=
c
(
(
p
+
q
)
m
o
d
k
)
。
直接令
c
1
c_1
c
1
为 FFT 中的范德蒙德矩阵即可,即
c
(
i
,
j
)
=
w
k
i
j
c(i,j)=w_k^{ij}
c
(
i
,
j
)
=
w
k
i
j
。
但在模意义下可能不存在
k
k
k
次单位根。
咕。