多元函数的向量表示_在线计算专题(09)：向量的基本属性与各类常见运算及几何应用实现方法…

本文将以实例的形式，基于Wolfram Alpha计算搜索引擎，介绍高等数学、线性代数与空间解析几何中涉及的向量的描述、向量的属性，向量的基本运算，向量间的相互关系，向量的数量积、向量积、混合积的计算及它们的几何应用相关问题的实现方法.

1、向量的基本属性与相互关系

例1 一般向量的基本属性. 参考输入表达式为

vector (a,b,c)

执行计算得到的结果显示如下.

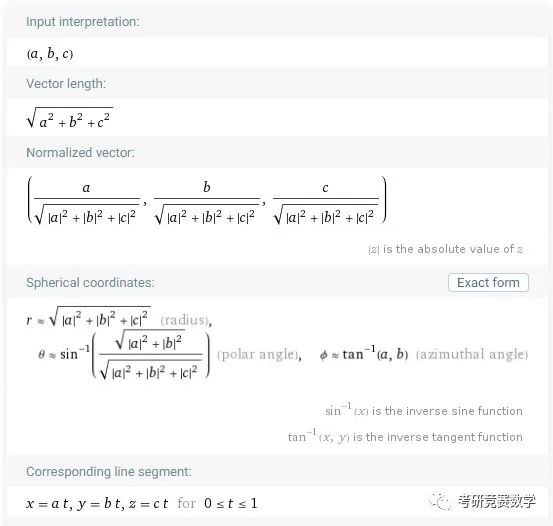
主要包括四个部分的结果：向量的模(长度)，单位化向量，向量在球坐标描述以及向径的参数方程描述. 输入具体的数值则将显示对应坐标对应的向径的图形演示. 如果输入多个向量，还会给出向量的线性相关性和形成的子空间描述形式.

【注】向量的坐标描述也可以用花括号描述，即“
{a,b,c}
”.

例2 考察向量, , 的基本属性和相互关系.

参考输入表达式为

vector (2,2,-3),(-3,1,3),(1,2,1)

执行计算得到的结果如下.

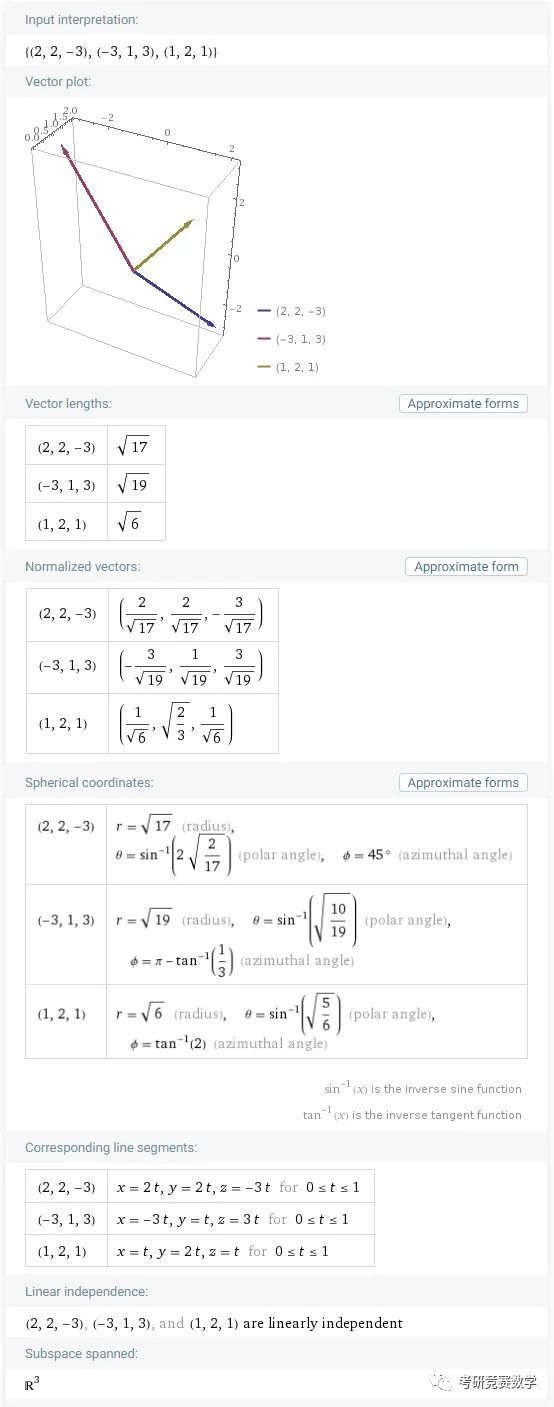
结果首先给出三个向量的向径图形描述形式、各向量的长度、对应的单位向量、球坐标描述与对应线段描述的参数方程表达式，然后讨论了向量组的线性相关性和可以构成的子空间，这里由于三个向量线性无关，又为三维向量，所以构成三维空间.

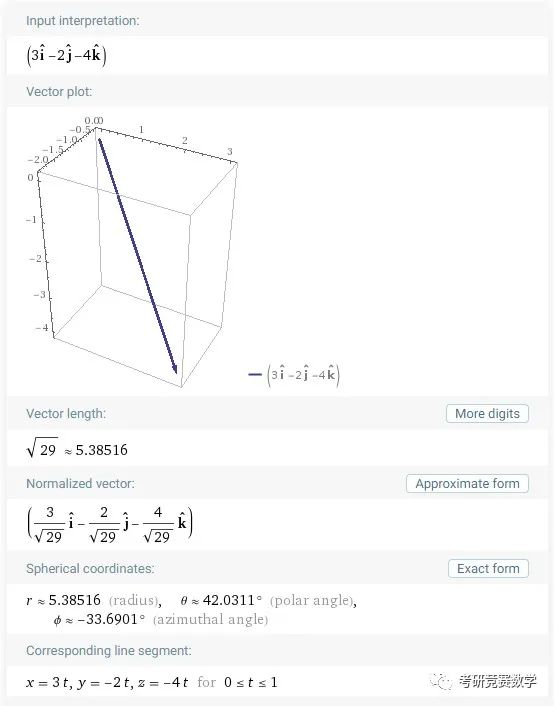
【注】对于具体数值描述的三维向量，也可以直接以基向量的描述形式输入，比如输入

vector 3i-2j-4k

执行计算后，得到与上面括号输入方式相同内容的显示结果，如下图所示.

2、向量的模、单位化直接计算

例1 求向量与的模.

参考输入表达式为

||(3,4)||,||(3,4,5)||

执行计算得到的结果如下.

用双竖线可以直接表示求模(范数). 也可以用
norm
替换，比如输入
norm (3,4)
，执行直接得结果为,；输入
norm (3,4,5)
，执行直接得结果.

例2 求向量的单位向量与方向余弦.

参考输入表达式为

normalize vector (a,b,c)

执行计算得到的结果如下.

结果不仅是是向量的单位向量，也是三个方向余弦构成的向量.

3、向量的线性运算

例1 求两点, 之间的距离.

两点之间的距离即两点构成的向量的向量的长度，参考输入表达式为

||(x2,y2,z2)-(x1,y1,z1)||

执行计算得到的结果如下.

将坐标用具体数值替换则得到具体点间的距离.

例2 求两点, 的中点的坐标.

参考输入表达式为

((2,3,5)+(-1,2,-3))/2

执行计算得到的结果如下.

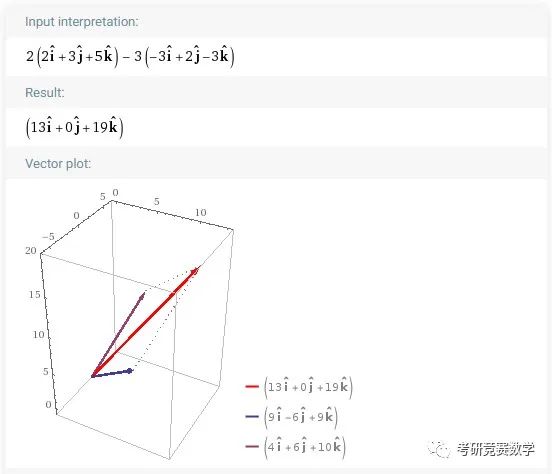
【注】向量的线性运算操作也可以用基向量描述形式操作，比如输入

2(2i+3j+5k)-3(-3i+2j-3k)

执行计算后得到

4、向量的数量积及其应用

例1 求两向量和的数量积.

参考输入表达式为

(x,y,z).(a,b,c)

执行计算得到的结果如下.

例2 已知三点, , ，求角∠ABC.

所求角即为向量, 所成的夹角，容易计算得到

参考输入表达式为

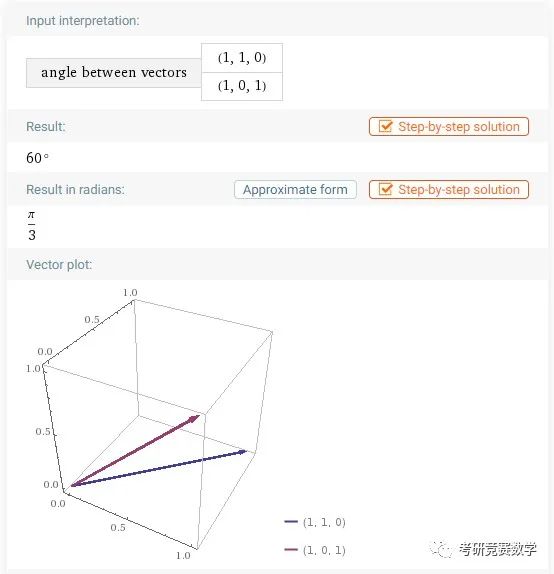
the angle of vector (1,1,0) ,(1,0,1)

执行计算得到的结果如下.

例3 求向量在向量上的投影与投影向量.

由投影计算公式，得

参考输入表达式为

((4,-3,4).(2,2,1))/||(2,2,1)||

执行计算得到的结果为. 为直接得到投影向量，输入如下表达式

projection {4,-3,4} on {2,2,1}

计算结果显示为

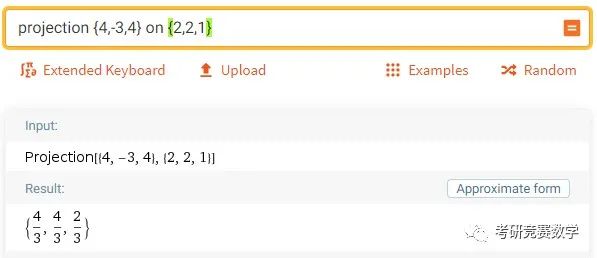
可得投影向量的模就为.

5、向量的向量积及其应用

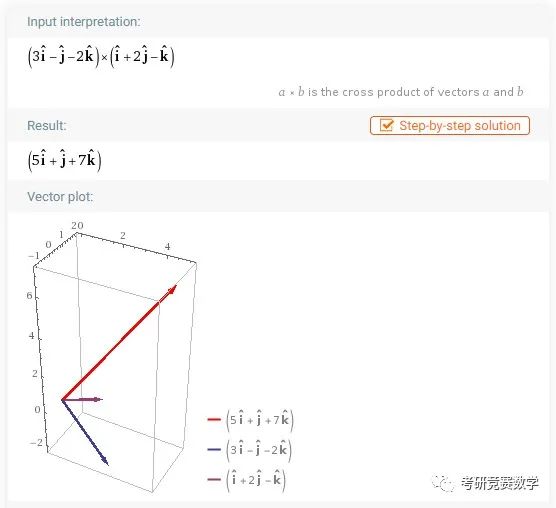
例1 求两向量的向量积，其中

参考输入表达式为

(3i-j-2k)x(i+2j-k)

其中叉乘符号直接输入字母“
x
”表示就行，一般不能正常计算时用
cross
替换，即输入

(3i-j-2k) cross (i+2j-k)

执行计算得到的结果如下.

【注】以上表达式也可以直接以坐标形式
(3,-1,-2)x(1,2,-1)
输入，得到结果也是坐标.

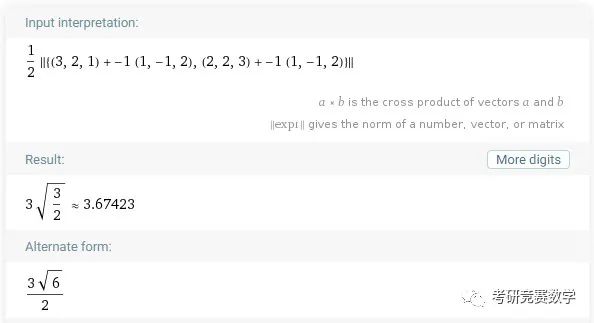
例2 求三角形的面积，三角形的三个顶点坐标为

由向量积的几何意义，可知三角形的面积为

||((3,2,1)-(1,-1,2)) cross ((2,2,3)-(1,-1,2))||/2

执行计算得到的结果如下.

6、向量的混合积及其应用

例1 求混合积，其中

参考输入表达式为

((a_1,a_2,a_3) cross (b_1,b_2,b_3)).(c_1,c_2,c_3)

执行计算得到的结果如下.

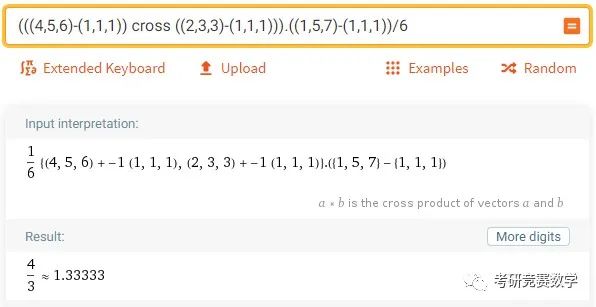
例2 求四面体的体积，其中四面体的四个顶点坐标分别为

由混合积的几何意义，可知四面体的体积计算公式为

所以参考输入表达式为

(((4,5,6)-(1,1,1)) cross ((2,3,3)-(1,1,1))).((1,5,7)-(1,1,1))/6

执行计算得到的结果如下.

在线计算专题推荐阅读：

专题(01)：大学数学中常用的初等数学计算实现方法
专题(02)：数列、一元、多元函数极限的计算与连续性判定
专题(03)：具体、抽象函数、隐函数、参数方程求导与方向导数计算
专题(04)：函数单调性判定、极值点、拐点、驻点、鞍点、极值与最值的计算
专题(05)：常微分方程、差分方程(递推数列)(组)通解、特解的计算
专题(06)：绘制函数、方程与不等式描述的平面、空间图形
专题(07)：不定积分、定积分与重积分、曲线、曲面积分的计算
专题(08)：泰勒公式、常值级数、幂级数与傅里叶级数求和与展开

微信公众号：考研竞赛数学(ID: xwmath)

大学数学公共基础课程分享交流平台！

支持咱号请点赞分享！

↓↓↓

点

查看更多相关内容

目录：

1、向量的基本属性与相互关系

2、向量的模、单位化直接计算

3、向量的线性运算

4、向量的数量积及其应用

5、向量的向量积及其应用

6、向量的混合积及其应用

你可能也喜欢