文章来源: 丁点帮你
作者:丁点helper

昨天的文章,我们对方差分析的整体逻辑进行了初步的介绍,今天将以单向(one-way)方差分析为例,具体梳理方差分析的整个过程。
单向(one-way)方差分析,就是大家很熟悉的单因素方差分析(教科书上叫单向), 一般也称完全随机设计(completely randomized design)的方差分析,是
指将研究对象通过完全随机化方法,分配至多个不同的处理组,比较多组的效应指标是否存在差别
。
先看如下案例:
为了解大骨节病与粮食中微量元素硒含量之间的关系,某研究团队调查了A(渭源县)、B(青州市)
两个大骨节病区
和C(泰山区)、D(长清区)
两个非大骨节病区
。
每个病区随机抽取20户农户并采集面粉,检测面粉中硒元素含量(μg/kg),试分析这4个地区面粉中硒含量是否存在差异。具体的数据情况如下表1。
表1 四地区面粉硒元素含量样本数据表
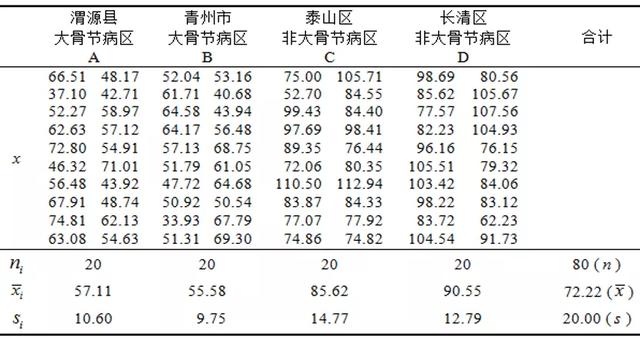
我们将上述数据绘制成图形(如下图,每个空心小圆圈代表一个样本值),可以很直观地看到,这80个样本值(20*4)各不相同,即它们存在差异。
暂时忽略其他潜在的混杂因素,这种差异的原因可能是由于它们来自不同的地区,但因为四个小组内部的数值也都一一不同,所以,差异也可能仅仅是因为随机误差,通俗地理解就是人们说的运气导致的。
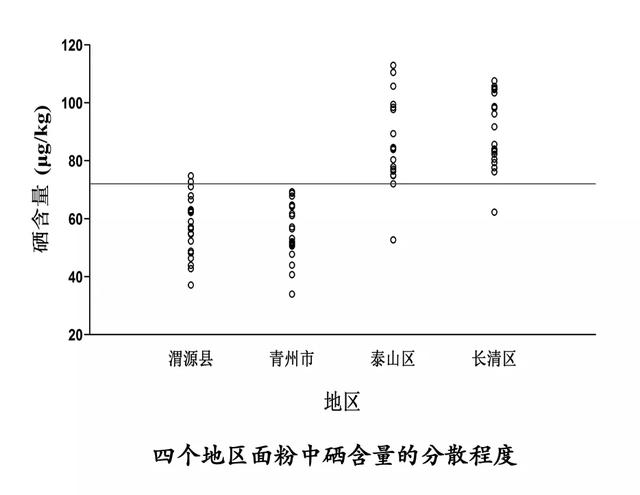
不过,仔细地观察发现两个病区的数据好像明显要低一些,这便提示地区的不同确实有可能造成了目前的差异。
为了验证我们的猜测,就可以采用方差分析来检验:
病区与非病区面粉硒含量的差异是否具有统计学意义。
这里需要再明确一点的是,我们的目标是比较这四个地区面粉中硒含量是否有差异,
在实际操作中,我们比较的是四个地区硒含量的总体平均数,因此,只要总体平均数有差异,我们就说四地区硒含量有差异。
要进行方差分析,当然,我们首先要进行假设:
这四组数据都没有差异,注意是都没有!
在这个假设下,我们可以把这四组数据看做是一个大组,即将上述80个数据视为一个整体。对于这个整体,我们可以计算一个平均数和标准差,即表1中72.22和20.00。
可是实际情况下,这80个数据是分属于四个小组的,因此我们也可以分别计算这四个小组的平均数,即57.11、55.58、85.62、90.55。
如果假设成立(即四组数据都没有差异),那么这四个小组的平均数应该是围绕着整体平均数(即72.22)上下波动的,互相差异应该不是很大。
但现在我们实际获得的数据却显示,小组中最低的均数为57.11、最大的为90.55,直观上看都与72.22的距离不小,所以我们就会怀疑不能把它们看做一个整体(更严谨的表达是,它们不是来自同一个总体),从而拒绝它们相同的假设。
顺着这个思路,我们获得下面这张表格(表2):
表2 方差分析一般结果表

上述表格中涉及的具体的计算过程大家不需要细看,只需大概了解所谓的“离均差平方和(SS)”和“均方(MS)”的计算方法。
然后对照前面我们谈到的方差的概念和计算方法,你是否会发现,不明所以的
“均方(MS)”其实可以看做是一种特殊类型的“方差”
!
对照下图方差的计算公式:左边是离均差平方和,右边是自由度。
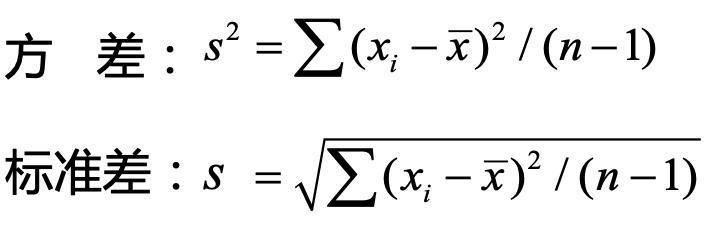
我们首先看衡量“组内变异”的均方(MS组内),在各个小组内部因为没有地区差异,所以MS组内的大小大小仅反映了随机误差(即运气)的情况。
而当假设四组总体均数相同时,组间均方(MS组间)的大小也仅仅反映随机误差的大小。
如何理解这里的谈到的“随机误差”呢?
对于来自同一个总体的两个或多个样本的差异我们可以简单理解为
随机误差
,也就是说,虽然表面上它们不同,但这种不同并没有意义,也不会反映额外的信息,仅仅是因为运气导致的。
好比你和别人掷色子比大小,虽然你们获得的点数不同,但这种不同完全是因为运气,不能说明任何其他的问题,同时也不会出现一个人总赢、另一个总输的局面。
但是如果对方悄悄在色子上做了点手脚,知道怎样掷可以获得大的点数,这个时候,
你们点数的差异就不再仅仅因为运气,还有色子的原因。
用统计学的语言来说,就是你们的差异不仅包含了随机误差,还包含了其他因素。所以,下次如果感觉自己总是在输,就要看看是不是色子出现了问题。
回到本例,既然MS组间和MS组内这两者都仅反映随机误差的大小,那么其携带的信息量就应该没有差异(提示:方差的大小决定了数据的信息量)。
由此,
在数值上MS组间与MS组内差异不大,所以使用MS组间除以MS组内时,所获得F值原则上应该在1附近
。
如果现在我们获得的数据计算出来的F值比1大很多(对应的P值会很小),
则意味着MS组间远大于MS组内
,从而表示,MS组间携带了多余的信息,因此,可以证明MS组间的差异不仅仅包含随机误差,还包含其他因素(比如地区不同),结合本例,即意味着四地区间面粉硒含量不都相同!
将上述数据用SPSS运算后获得结果如下表3。很显然,F值超过46,远大于1(注意,在正式情况下F值并非和1比较,这里仅为了方便理解),其对应的P值远小于0.05,由此拒绝零假设,差异有统计学意义,可以认为这四个地区硒含量的总体均数不全相等,也就是说至少有两个地区总体均数不等。
表3 四地区硒含量方差分析结果表

单向方差分析仅告诉我们这四个总体均数不全相等,但具体哪几个不等,哪几个相等呢?这就涉及到两两比较了,这就是我们明天的内容。