-
利用统计学方法进行:
描述统计
(利用图表形式对数据进行汇总和展示,包括计算一些统计量如均值、方差、比率等;描述统计包括:
图表描述,统计量描述
)
和
推断统计
(主要利用样本信息推断总体特征,主要包含两类一类是
参数估计(
利用样本信息推断所关心的总体特征
),一类是
假设检验
(
利用样本信息推断总体的某个假设是否成立
))
。
-
变量:描述所观察事物的某种特征;
类别变量(定性变量):无序类别变量,有序类别变量
数值变量(定量变量):离散变量,连续变量
-
数据:变量的观测值。
数据来源:二手数据,亲自调查,概率抽样,简单随机抽样,分层抽样,系统抽样(等
距抽样),整群抽样。
- R的基本数据类型:
数值型:
a<-c(2,5,8,3,9)
字符型:
b<-c(”
甲
“,”
乙
“,”
丙
“,”
丁
“)
逻辑型:
c<-c(“TRUE”,”FALSE”,”FALSE”,”TRUE”)
因子型
- R的基本数据结构:
向量:
一些创建向量的方法:
v1<-1:6 # 产生1~6
的等差数列
v2<-seq(from=2,to=4,by=0.5) #
在
2~4
之间产生步长为
0.5
的等差数列
v3<-rep(1:3,times=3) # 将1~3
的向量重复
3
次
v4<-rep(1:3,each=3) # 将1~3
的向量中每个元素重复
3
次
矩阵:
a<-1:6 # 生成1
到
6
的数值向量
mat<-matrix(a, nrow=2, ncol=3, byrow=TRUE)
rownames(mat)=c(“甲”,”乙”)
#
添加行名
colnames(mat)=c(“A”,”B”,”C”) # 添加行名
# 用t
函数对矩阵转置
t(mat) # 矩阵转置
数组
数据框:
# 写入姓名和分数向量
names<-c(“刘文涛
“,”
王宇翔
“,”
田思雨
“,”
徐丽娜
“,”
丁文斌
“) #
写入姓名向量
stat<-c(68,85,74,88,63) #写入各门课程分数向量
math<-c(85,91,74,100,82)
econ<-c(84,63,61,49,89)
# 将向量组织成数据框形式
table1_1<-data.frame
(
学生姓名
=names,
统计学
=stat,
数学
=math,
经济学
=econ)
因子 factor
列表
-
R数据查看:head(t,3), tail(t,3), nrow(t), ncol(t) dim(t), class(t), str(t)#查看t的数据结构
- 选中数据框中特定列:mean(df$统计学), mean(df[,1])
- 读取R数据:load(“t.RData”)
- 保存为R数据:save(matrix1,file=”./data/mat.RData”)
- 读取含标题csv文件:t<-read_csv(“1.csv”)
- 读取不含标题的csv文件:t<-read_csv(“1.csv”,header=FALSE)
-
保存csv文件:
write.csv
(t,file=”1.csv”) - 读取xlsx文件:t<-read_excel(“1.xlsx”,as.data.frame=TRUE)
- 保存.xlsx文件:write_xlsx(x=t,”./data/1.xlsx”)
-
数据排序:table=Table[order(Table$数学,decreasing=TRUE),]#降序
-
table=Table[order(
–
Table$数学),]#降序 - table=Table[order(Table$数学),]#升序
-
table=Table[order(
-
对矩阵行或者列求和
- colSums(t[,1:5])
- rowSums(t)#对t的每一行求和
- rbind(t,totals=colSums(t[,1:5]))#将1-5列求和的结果命名为totals并以行添加到t中
- cbind(t,totals=rowSums(t[1:10,]))#将1-10行的求和结果以列添加到t中
-
apply(matrix1_1,
1,
sum) #
对矩阵所有行求和
-
apply(matrix1_1,
2,
sum) #
对矩阵所有列求和
-
apply(matrix1_1, 1, mean)
-
apply(matrix1_1, 2, mean)
-
apply(matrix_1, 2,
sd
)
-
编辑数据框——变量重命名
-
rename(table1_1, c(
姓名
=”name”,
统计学
=”stat”))
- 缺失值处理
- x=c(1,2,NA)
- sum(x,na.rm=TRUE)
-
-
数据合并
- rbind(df1,df2)
- cbind(df1,df2[2:5])#按列合并数据
-
短格式->长格式
-
library(reshape2) #
加载
reshape2
包
-
tab.long
<-melt(table1_1,id.vars=”
姓名
“,variable.name=”
课程
“,value.name=”
分数
“)
#
融合
table1_1
与
id
变量,并命名
variable.name=”
课程
“,value.name=”
分数
”
-
-
·生成随机数
-
rnorm
(n, mean=0,
sd
=1)
-
#产生
n
个服从均值为
mean
,方差为
sd
正态分布的随机数
-
-
runif(n, min, max) #
产生
n
个在
min~max
之间服从均匀分布随机数
rexp(n) #
产生
n
个服从指数分布的随机数
rchisq(n,
df
) #
产生
n
个服从自由度为
df
的卡方分布的随机数
一维列联表
mytable1<-table(example1_1$社区);
mytable1
# 将频数表转化成百分比表
prop.table(mytable1)*100
•
二维列联表
# 生成社区和态度的二维列联表
mytable2<-table(example1_1$态度,example1_1$
社区
);mytable2
addmargins(mytable2) # 为列联表添加边际和
addmargins(prop.table
(mytable2)*100) #
将列联表转换成百分比表
抽样与数据筛选
简单随机抽样
samples(table1,10) #默认无放回
samples(table1,10,replace=TRUE) #有放回抽样
samples(table1$姓名[table1$成绩>90])#筛选出成绩大于90分的姓名
分层抽样
result=Strata(table1,stratanames=”姓名”,size=c(round(lenght(table1$性别[table1$性别==“男”])*0.2),round(lenght(table1$性别[table1$性别==”女”])*0.2)),method=”srswor”) #按照性别分层抽取20%样本
系统抽样
result=sampleBy(~1,frac=0.2,relpace=FALSE,data=table1,systematic=TRUE)
#~1表示数据没有分组,frac表述数据抽样的间隔1/0.2=5个,replace=FALSE表示无放回抽样,systematic=TRUE表示做系统抽样。
•
将列联表转换为原始数据
library(DescTools)
mytable<-
ftable
(example1_1,row.vars=c(”
社区
“),
col.vars
=c(”
性别
“,”
态度
“))
# 将列联表转化成原始数据框
df<-
Untable
(
mytable
)
head(df,3)
# 将列联表转换成带有交叉频数标签的数据框
dff<-
as.data.frame
(mytable)
数值数据如何生成生成频数分布表
确定要分组的组数:
大致计算出组数。
确定各组的组距
统计出各组的频数
library(DescTools)
example1_2<-read.csv(“.//data//example//chap01//example1_2.csv”)
tab<-
Freq
(example1_2$
销售额
); tab
或者
# 指定组距,不含上限值
tab1<-Freq(example1_2$销售额,breaks=c(160,175,190,205,220,235,250,265,280),
right=FALSE
)
tab2<-data.frame(
分组
=tab1$level,
频数
=tab1$freq,
频数百分比
=tab1$perc*100,
累积频数
=tab1$sumfreq,
累积百分比
=tab1$sumperc*100) #
重新命名频数表中的变量
基本绘图函数
graphics
包中的绘图函数大致可分为两大类:一类是
高级绘图函数
,这类函数可以产生一幅独立的图形;另一类是
低级绘图函数
,这类函数通常不产生独立的图形,而是在高级函数产生的图形上添加一些新的图形元素,如标题、文本注释、线段等
plot
函数
是
graphics
包中最重要的高级绘图函数,它是一个泛函数,可以绘制多种图形。给函数传递不同类型的数据,可绘制不同的图形。除
plot
函数外,
graphics
包中还有其他一些高级绘图函数,如绘制条形图的
barplot
函数
,绘制直方图的
hist
函数
,绘制箱线图的
boxplot
函数
,等等。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
低级绘图函数中,有为图形添加图例的
legend
函数
、页面布局的
layout
函数
、为图形添加注释文本的
mtext
函数
,等等。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
绘图
##绘制2*2的图,第二列为1个图
#设置布局环境,2*2,宽度比为2:1
dev.new()
layout(matrix(c(1,2,3,3),nrow=2,ncol=2),widths=c(2,1))
#设置图形边框,文字和绘图符号大小
par(mai=c(0.6,0.6,0.1,0.1),cex=0.7)
#mai表示设置图形边距大小c(底部,左侧,上方,右侧),cex控制文字和绘图符号的大小
x=rnorm(5000) #标准正态分部
y=rchisq(5000,10) #卡方分布
hist(x,prob=TRUE,col="lightblue",xlab="x",ylab="Density",ylim=c(0,0.4),main="")
hist(y,freq=TRUE,col="pink",xlab="y",ylab="Density",main="")
boxplot(x,col="red",lwd=1)•
type(“p”
,
“l”
,
“o”
,
“b”,
“s”
,
“h”
,
“n“)
•
O
画点,
b
画点连线,
h
画点的垂线,
n
啥也不画空坐标
•
xlab
,
ylab
,
xlim,ylim
(坐标轴)
•
main, sub(
标题)
•
lwd
(
线宽
), col(
颜色
),
pch
(
点样子
),
lty
(
线性
)
•
ann
(
是否绘制坐标轴的标签和图形的标题
)
•
axes(
是否绘制坐标轴,
禁用全部坐标轴,框架和刻度全部没有
)
•
xaxt
=“n”
禁止
x
轴的刻度线,
yaxt
=”n”
禁止
y
轴的刻度线
title(main=“My Title”
,
sub=“sub-title”,
xlab
=“…”,
ylab
=“…”
axis(
side=
,
at=
,
labels=
,
pos
=,
lty
=, col=,
las
=
,
tck
=,……)
text(location, “text to place”,
pos
, ………) #
图里面的点添加文字
mtext
(“text to
place”,side
, line=n ,………) #
图外面的边框添加文字
legend(location=, title=, legend,…………)

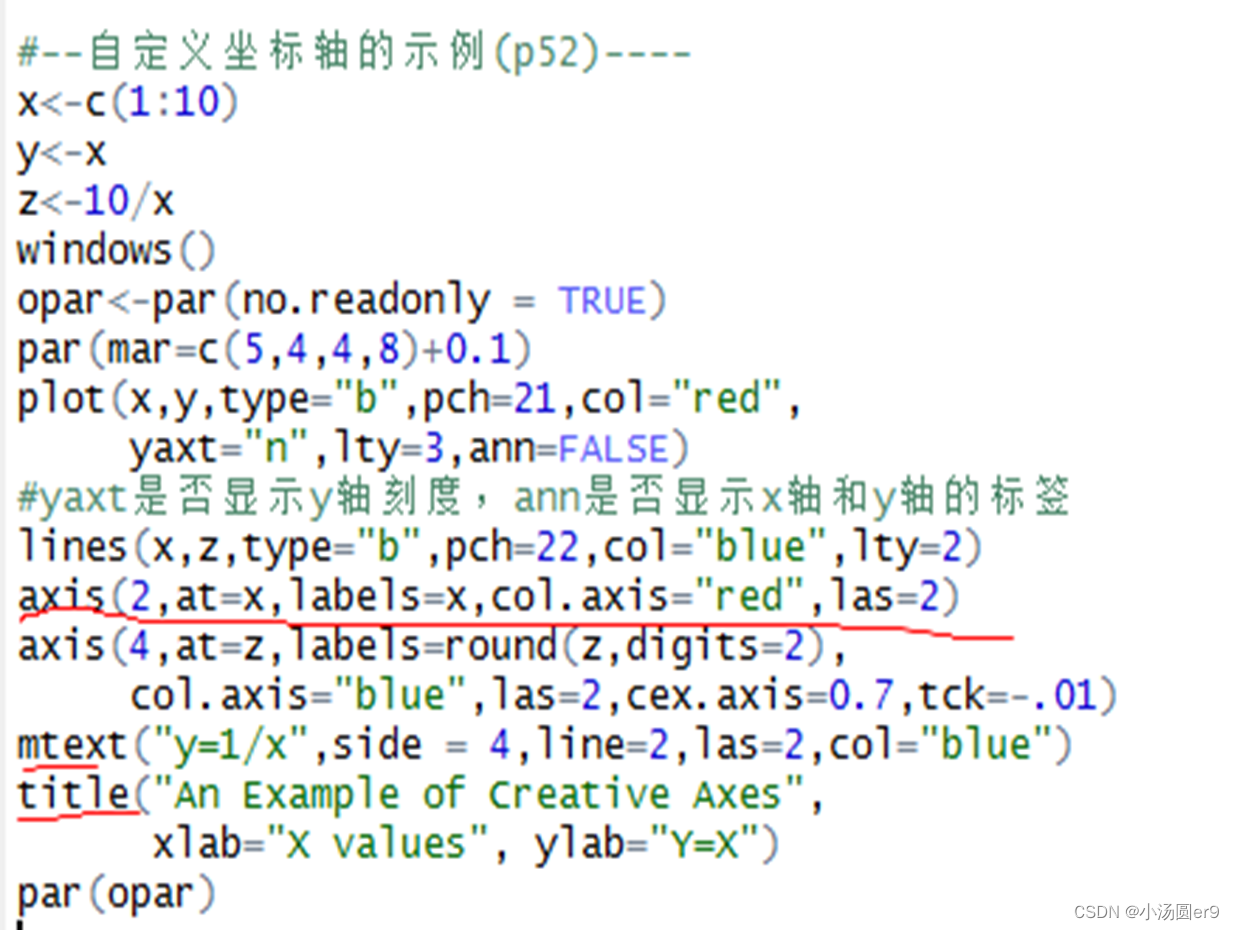


直方图:
用矩形的宽度和高度来表示频数分布,通过直方图可以观察出数据的大致分布情况如是否对称。
hist(table$销售额,xlab=”x”,ylab=”y”,main=”销售额”)
hist(table$销售额, breaks=20,xlab=”x”,ylab=”y”,main=”销售额(分成20组)”)
hist(table$销售额,prob=TRUE,breaks=20,xlab=”x”,ylab=”y”,main=”销售额分成20组加上核密度线”)
lines(density(table$销售额),col=”red”)
hist(table$销售额,prob=TRUE,breaks=20,xlab=”x”,ylab=”y”,main=”销售额分成20组加上正态分布曲线”)
curve(dnorm(x,mean(table$销售额),sd(table$销售额),add=T,col=”red”))
茎叶图
反映数据的分布特征,且能保留原始数据的基本信息。,当数据较少时,用茎叶图更容易观察数据的分布。
箱线图
反映一组数据的分布特征,还可以用于多组数据分布特征进行比较。
小提琴图
(将分布的核密度曲线和与箱线图结合在一起,在箱线图上以镜像的形式叠加一条核密度估计曲线)从核密度估计曲线可以大致看出数据的形状。
三、数据的描述统计量
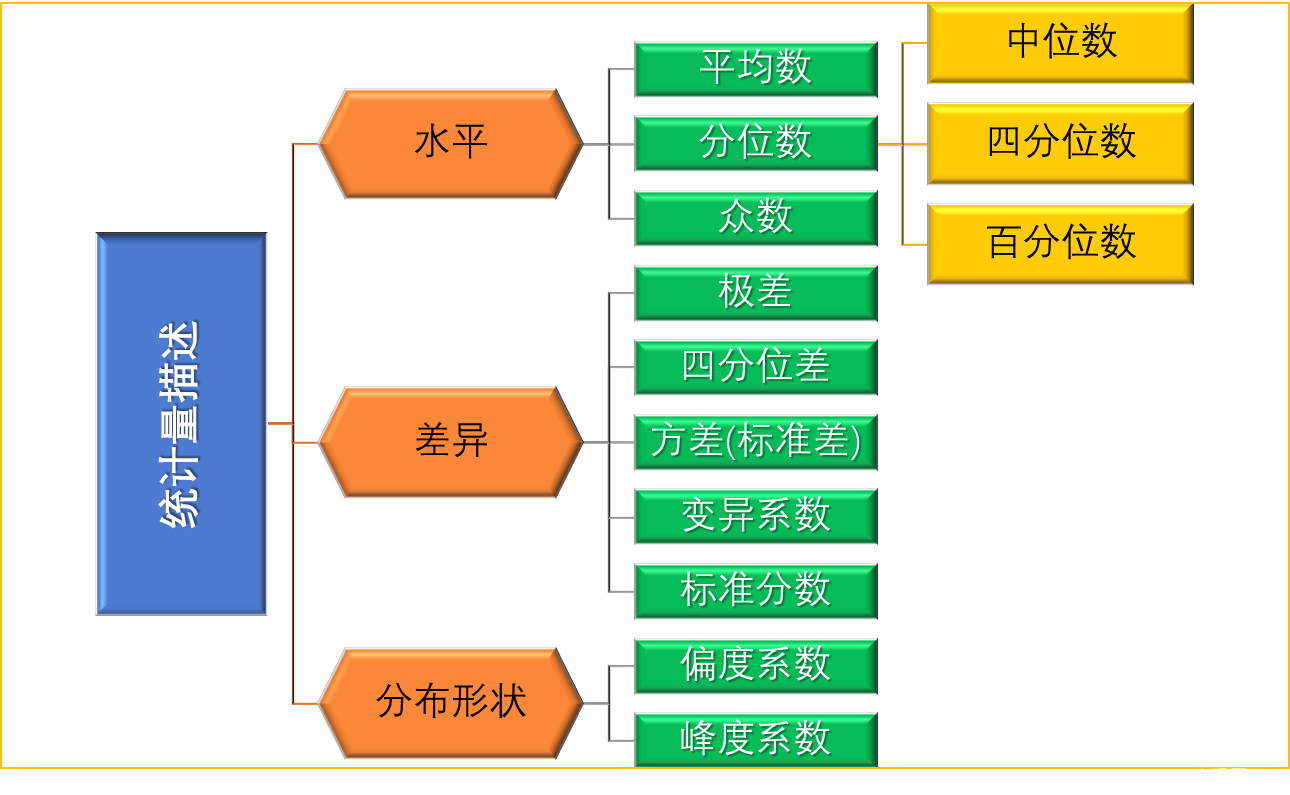
描述水平的统计量——平均数
能够反映数据的总体特征
·
消除了观测值的随机波动,容易受到极端值的影响。
由总体计算出来的均值称为总体均值
(mu)
,用样本数据计算出来的均值称为样本均值(x_bar)
计算普通均值:mean(table$成绩)
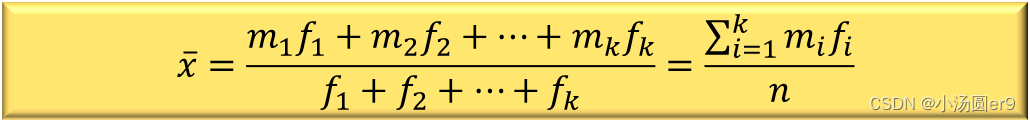
计算加权均值:
weighted.mean(table$组中值,table$人数)
,公式中mi表示组的平均数,fi表示频数。
描述水平的统计量——分位数
将数据按
从小到大排序
后,位于某一位置上的数值,分位数有:中位数,(上/下)四分位数,百分位数。
分位数不受极端值的影响,在研究收入分配时很有用
。
中位数计算: median
median(table$销售额)
25%位置为下四分位数,75%称为上四分位数
四分位数位置的计算:
Q25%的位置=(n+1)/4 , Q75%的位置为=3(n+1)/4,当计算出的位置不是整数时,若小数位是0.5则取两边数值的平均数作为分位数;若是0.25则应在整数位置(m)的
数值上加0.25*(值m+1-值m)
。
quantile(table1$销售额,probs=c(0.25,0.75),type=6)
描述水平的统计量——百分位数
将数据用99点均分为100份,处于各个位置的数值就是对应的分位数;
反映了各项数据在最大数据与最小数据之间的分布关系
。
描述差异的统计量
差异量反映了数据的离散程度,描述差异的统计量值越小说明描述水平的统计量数据的代表性就越好,反之说明描述水平的统计量对该数据的代表性就越差。
描述差异的统计量——极差(全距)
最大值与最小值之差,容易受到极端值的影响,不能全面反映差异情况。
描述差异的统计量——四分位差
上四分位数-下四分位数,反映了中间50%数据的离散程度,能够说明中间数据的集中情况,不受极端值的影响。
描述差异的统计量——平均离差
(数据与均值之差称为离差)
将离差取取绝对值后在平均
描述差异的统计量——方差
(
var
)
将离差平方取平均后在平均(分母是
n-1
)
描述差异的统计量——标准差
(
sd
)
将方差开方,标准差与原始数据的单位相同,其实际意义要比方差清楚,因此实际问题时常常使用标准差。
方差和标准差存在的问题: 当数据的观测值越大时,方差和标准差的值也会越大,采用不同的计量单位计算出的方差和标准差不一样,对于不同样本的数据,若数据的观测值相差较大或者计量单位不同时不能使用标准差直接比较离散程度。
描述差异的统计量——变异系数
CV
数据
标准差/均值
,主要用于比较不同样本数据的离散程度,变异系数越小说明数据的相对离散程度越小,数值越大说明数据的相对立离散程度越大;
消除了数值大小和计量单位对标准差的影响,反映了一组数据的相对离散程度
。
描述差异的统计量——
标准分数
z
也称z分数或者标准化值,用于度量数值在数据中的相对位置,并判断一组数据是否有离群点,可以把数据转化均值为0,标准差为1的新数据。计算方法为:zi=(xi-x_bar)/s (数据与平均值相差几倍方差)
描述
分布形状
的统计量——
偏度系数
SK (
skewness(table1$销售额)
)
偏度是指数据分布的不对称性,测量数据的分布不对称性的统计量称为偏度系数SK,若取值大于1或者小于-1则称为
严重偏斜分布
,若-1<SK<-0.5或者0.5<SK<1则称为
中等偏斜分布
,若-0.5<SK<0.5则称为
轻微偏斜
。取负值表示
左偏分布
(左侧有长尾),取正值表示右偏分布(右侧有长尾);
越接近于零表示越接近对称分布
。
描述
分布形状
的统计量——
峰度系数
K (
kurtosis(table1$销售额)
)
峰度是指数据分布峰值的高低(通常与标准正态分布相比较而言),测度一组数据分布峰值高低的统计量称为峰度系数。当K大于零时为尖峰分布,数据分布的峰值比标准正态分布高,数据相对
集中
;K<0时为扁平分布,数据分布的峰值比标准正态分布低,数据较为
分散
。
四、随机变量的概率分布
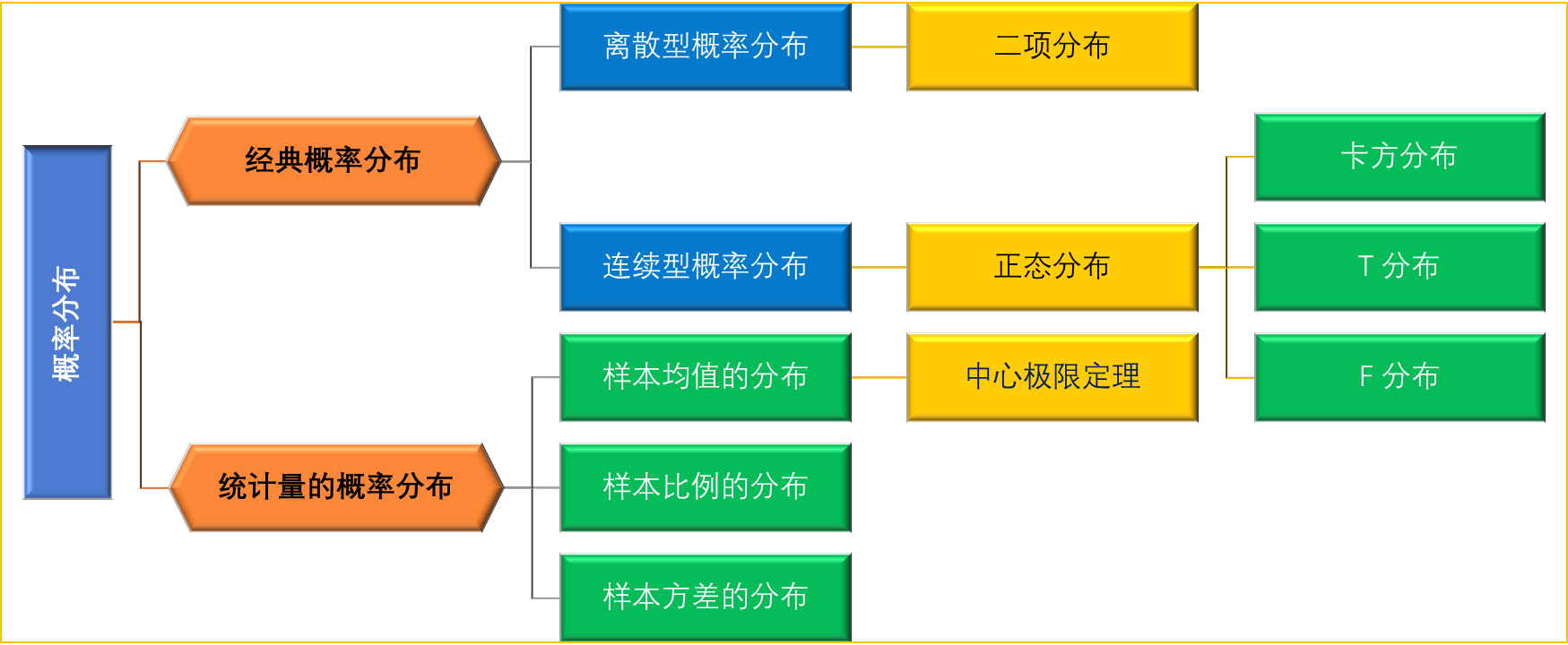
离散型随机变量 (二项分布,泊松分布,超几何分布)
随机变量 X 取有限个值或所有取值都可以逐个列举出来
以确定的概率取这些不同的值
连续型随机变量 (连续型概率分布:正态分布,均匀分布,指数分布)
可以取一个或多个区间中任何值
所有可能取值不可以逐个列举出来,而是取数轴上某一区间内的任意点
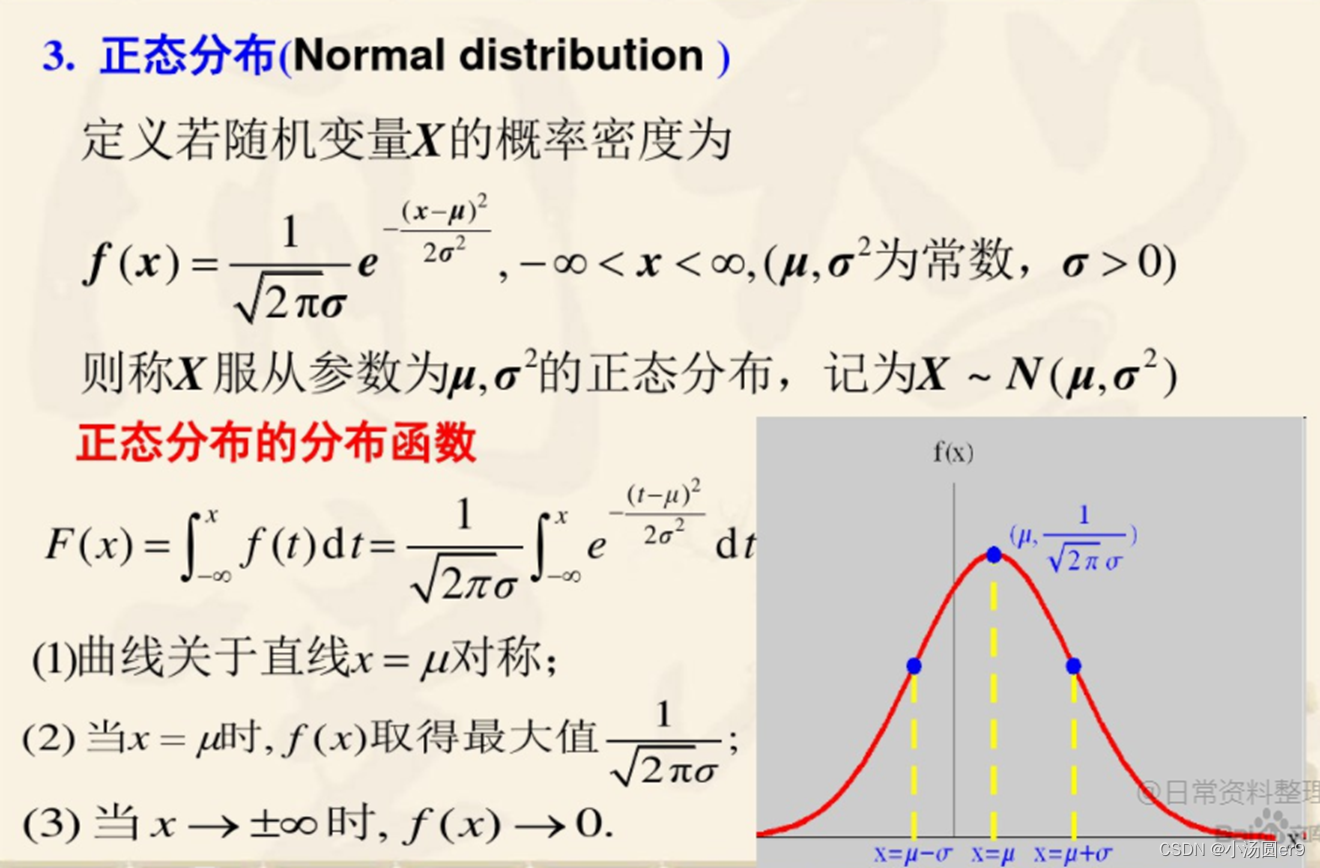
在n次伯努利实验中成功x次的概率
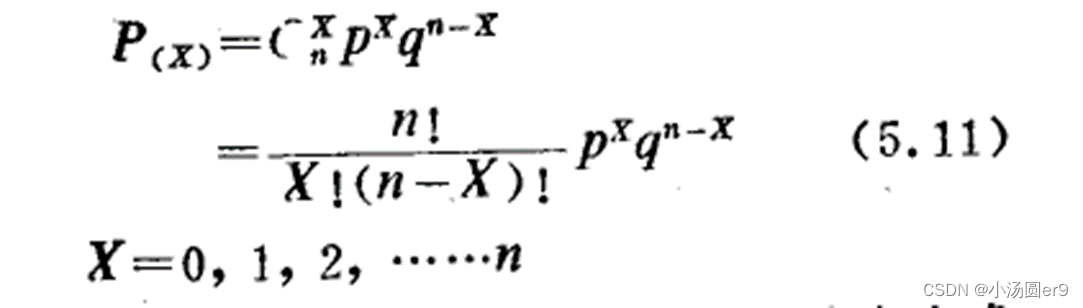





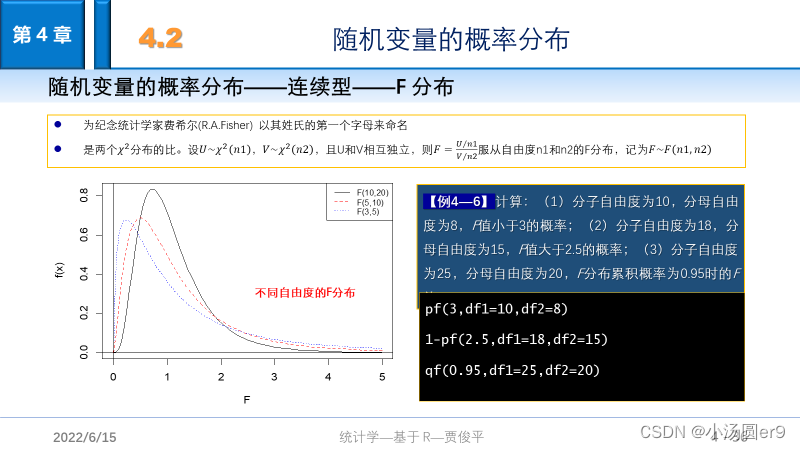


标准差是根据原始观测值计算出来的,反映了原始数据的离散程度,而标准误是根据样本统计量计算出来的,反映的是统计量的离散程度。标准误越小,表名样本统计量与总体参数的值越接近,样本对总体越具有代表性。
中心极限定理
:如果总体不是正态分布,随着样本量n的增大,样本均值的概率分布仍趋于正态分布,其分布的期望值为总体均值mu,方差为总体方差的1/n。
五、参数估计
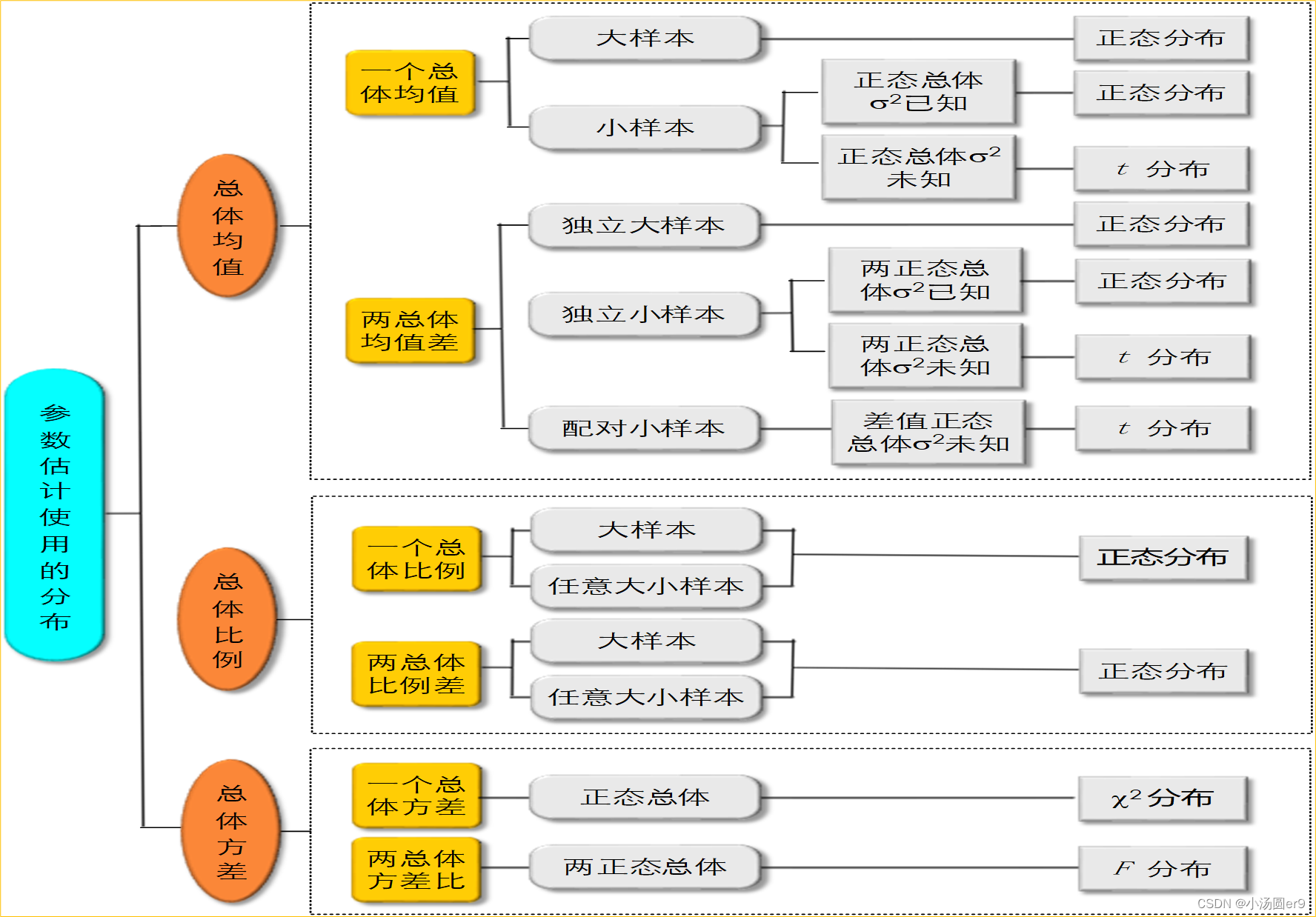
l
参数估计
(parameter estimation)——
就是用
样本统计量
去估计
总体的
参数。
l
估计量
:用于估计总体参数的统计量的名称。如:样本均值,样本比例,样本方差等。
Ø
样本均值
就是总体均
值
?
μ
的一个
估计量
Ø
参数
用
q
表示,估计量
用
?
θ ̂
表示
l
l
估计值
——
估计参数时计算出来的统计量的具体
值
Ø
如果样本均值
?
=80
x ̅=80
,则
80
就是
q
的估计值
l
分类:
点估计
和
区间估计
l
点估计
——
用样本的估计量的某个取值直接作为总体参数的估计值
例如:用样本均值直接作为总体均值的估计;用两个样本均值之差直接作为总体均值之差的
估计
l
点估计无法给出估计值接近总体参数程度的信息
由于样本是随机的,抽出一个具体的样本得到的估计值很可能不同于总体真值
一个点估计量的可靠性是由它的标准误来衡量的
,这表明一个具体的点估计值无法给出估计的可靠性的度量
l
区间估计
——
在点估计的基础上,给出总体参数估计的一个估计区间,该区间由样本统计量加减估计误差而
得到
。
如果将构造置信区间的步骤重复多次,置信区间中包含总体参数真值的次数所占的比例称为
置信水平
,也称为
置信度
或
置信系数(
confidence coefficient
)
l
置信区间
—
由样本估计量构造出的总体参数在一定置信水平下的估计区间
。统计学家在某种程度上确信这个区间会包含真正的总体参数,所以给它取名为置信区间
l
如果用某种方法构造的所有区间中有
95%
的区间包含总体参数的真值,
5%
的区间不包含总体参数的真值,那么,用该方法构造的区间称为置信水平为
95%
的置信区间。同样,其他置信水平的区间也可以用类似的方式进行表述
l
总体参数的真值是固定的,而用样本构造的区间则是不固定的,因此置信区间是一个
随机区间
,它会因样本的不同而变化,而且不是所有的区间都包含总体参数
实际估计时往往只抽取一个样本,此时所构造的是与该样本相联系的一定置信水平(比如95%)
下的置信区间。我们希望这个区间是大量包含总体参数真值的区间中的一个,但它也可能是少数几个不包含参数真值的区间中的一个,当抽取一个具体的样本,用该样本所构造的区间是一个特定的常数区间,无法知道这个样本所产生的区间是否包含总体参数的真值,它可能是包含总体均值的区间中的一个,也可能是未包含总体均值的那一个
一个特定区间总是“包含”或“绝对不包含”参数的真值,不存在“以多大的概率包含总体参数”的问题
置信水平只是告诉我们在多次估计得到的区间中大概有多少个区间包含了参数的真值
,而不是针对所抽取的这个样本所构建的区间而言的
•估计量的评价标准:
无偏性
:指估计量
抽样分布
的期望值(E(
))等于被估计的总体参数(
)。则称
是
的无偏估计。
有效性
:估计量的方差大小。
一致性
:随着样本无限增大,统计量收敛于所估计的参数。
#总体均值的置信区间(大样本)
setwd("E:\\大三下学期\\R\\R_code\\data\\data\\")
t1=read.csv(".\\example\\chap05\\example5_1.csv")
install.packages("BSDA")
install.packages("BSDA")
library(BSDA)
z.test(t1$耗油量,mu=0,sigma.x=sd(t1$耗油量),conf.level=0.9)
#一个总体均值的置信区间(小样本,方差未知)
t1=read.csv(".\\example\\chap05\\example5_2.csv")
t.test(t1,conf.level=0.9)
#计算两个总均值之差的置信区间(大样本)
t1=read.csv(".\\example\\chap05\\example5_3.csv")
z.test(t1$男性工资,t1$女性工资,mu=0,sigma.x=sd(t1$男性工资),sigma.y=sd(t1$女性工资),conf.level=0.95)$conf.int
#上面只显示95置信水平下的置信区间
#计算两个总体均值之差的置信区间(小样本)
#假设方差相等
t1=read.csv(".\\example\\chap05\\example5_4.csv")
t.test(t1$方法一,t1$方法二,var.equal=TRUE,conf.level=0.95)
#假设方差不等
t.test(t1$方法一,t1$方法二,var.equal=FALSE,conf.level=0.95)
#配对样本估计(大样本用z检验,小样本用t检验)
t1=read.csv(".\\example\\chap05\\example5_5.csv")
t.test(t1$试卷A,t1$试卷B,paired=TRUE)
#z.test(t1$差值d,mu=mean(t1$差值d),sigma.x=sd(t1$差值d))
#z检验书上没有,应该是这样写,不用记这一个
#总体比例的区间估计(大样本)
#某城市想要进行一项交通措施改革,为征求市民对该项改革措施的意见,
#在成年人中随机调查了500个市民,其中325人赞成改革措施。用97.5%的
#置信水平估计该城市成年人口中赞成该项改革的人数比例的置信区间
n=500
x=325
p=x/n
q=qnorm(0.975)
#95%的置信水平,则alpha=0.05,那么在计算分位数时应该
#计算1-alpha/2位置的分位数,也就是0.975
LCI=p-q*sqrt(p*(1-p)/n)
UCI=p+q*sqrt(p*(1-p)/n)
data.frame(LCI,UCI)
#结果是:0.6081925 0.6918075
#任意大小样本的比例估计(最重要的是n,p的更换后的定义)
n=500+4
x=325+2
p=x/n
q=qnorm(0.975)
#95%的置信水平,则alpha=0.05,那么在计算分位数时应该
#计算1-alpha/2位置的分位数,也就是0.975
LCI=p-q*sqrt(p*(1-p)/n)
UCI=p+q*sqrt(p*(1-p)/n)
data.frame(LCI,UCI)
#结果是:0.6071358 0.6904833
#两个总体比例的置信区间估计
#在某个电视节目的收视率调查中,女性观众随机调查了500人,
#有225人收看了该节目;男性观众随机调查了400人,有128人
#收看了该节目。用95%的置信水平估计女性与男性收视率差值的置信区间
#利用大样本的估计方法
n1=500
n2=400
x1=225
x2=128
p1=x1/n1
p2=x2/n2
q=qnorm(0.975)
LCI=p1-p2-q*sqrt(p1*(1-p1)/n1+p2*(1-p2)/n2)
UCI=p1-p2+q*sqrt(p1*(1-p1)/n1+p2*(1-p2)/n2)
data.frame(LCI,UCI)
#结果是:0.06682346 0.1931765,
#需要注意在计算两个总体的上下置信区间时需要p1-p2
#利用任意样本的区间估计
n1=500+2
n2=400+2
x1=225+1
x2=128+1
p1=x1/n1
p2=x2/n2
q=qnorm(0.975)
LCI=p1-p2-q*sqrt(p1*(1-p1)/n1+p2*(1-p2)/n2)
UCI=p1-p2+q*sqrt(p1*(1-p1)/n1+p2*(1-p2)/n2)
data.frame(LCI,UCI)
#结果是:0.06624396 0.1923634
#特别注意在比例区间估计中q的计算是1-alpha/2
六、假设检验

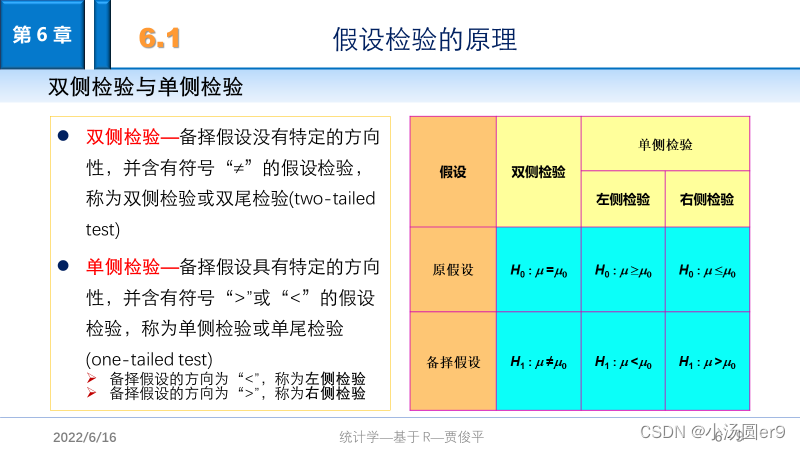
概率P小于显著性水平则拒绝H0
单样本t检验效应量的计算公式为:d=|样本均值-假设的总体均值|/样本标准
差
,0.2<d<0.5是小的效应量,0.5<d<0.8是中的效应量,d>0.8是大的效应量
library(lsr)
cohensD(t1$厚度,mu=5)#一个总体的效应量
cohensD(t1$甲企业,t1$乙企业)#两个独立样本t检验的效应量
cohensD(t1$旧款饮料,t1$新款饮料,paired=TRUE)#配对样本t检验的效应量




#一个总体均值检验(大样本):当备择检验是mu小于81时
library(BSDA)
z.test(t1$数据,mu=81,sigma.x=sd(t1$数据),alternative="less",conf.level=0.95)
#因为备择假设是小于,所以用alternative="less"
#一个总体均值检验(小样本)
t.test(t1$数据,mu=81)
library(lsr)
cohensD(t1$数据1,mu=81)
#两个总体均值之差检验(大样本),当备择假设是不等于号时
z.test(t1$数据1,t1$数据2,sigma.x=sd(t1$数据1),sigma.y=sd(t1$数据2),alternative="two.sided")
#两个总体均值之差检验(小样本),方差相等
t.test(t1$数据1,t1$数据2,var.equal=TRUE)
#两个总体均值之差检验(小样本),方差不相等
t.test(t1$数据1,t1$数据2,var.equal=FALSE)
#效应量计算
library(lsr)
cohensD(t1$数据1,,t1$数据2)
#配对样本检验
t.test(t1$数据1,t1$数据2,paired=TRUE)
#计算效应量
library(lsr)
cohensD(t1$数据1,t1$数据2,method="paired")
#一个总体比例的检验
#备择假设是pai>0.25
n=2000
p=450/2000
pi0=0.25
z=(p-pi0)/sqrt(pi0*(1-pi0)/n)
p_value=1-pnorm(z) #因为备择假设是>0.25
data.frame(z,p_value)
#两个总体比例之差的检验(pi1-pi2=0)
n1=200
n2=200
p1=0.27
p2=0.35
p=(p1*n1+p2*n2)/(n1+n2)
z=(p1-p2)/sqrt(p*(1-p)*(1/n1+1/n2))
p_value=pnorm(z)
data.frame(z,p_value)
#两个总体比例之差的检验(pi1-pi2=d0)
n1=300
n2=300
p1=33/300
p2=84/300
z=(p1-p2-d0)/sqrt(p1*(1-p1)/n1+p2*(1-p2)/n2)
p_value=pnorm(z)
data.frame(z,p_value)
#一个总体的方差检验
#假设备择假设是大于16
sigma.test(t1$数据,sigmasq=16,alternative="greater")
#两个总体的方差检验
#假设备择假设是不等于
var.test(t1$数据1,t1$数据2,alternative="two.sided")
八、方差分析
方差分析是分析
类别自变量
对
数值因变量
影响的一种统计方法,(自变量对因变量的影响简称效应),方差分析是通过对数据误差的分析来检验这种效应是否显著,分析数据处理误差是否显著存在。

#第八章代码
##实验8.2:单因子方差分析
#假设不同管理者对评分影响的效应量分别为alpha1,alpha2,alpha3
#H0:alpha1=alpha2=alpha3
#H1:alpha1!=alpha2!=alpha3
setwd("E:\\大三下学期\\R\\R_code\\data\\data\\")
T1<-read.csv(".\\exercise\\chap08\\exercise8_2.csv")
#将短格式数据改为长格式
library(reshape)
T2=melt(T1,variable_names="评分")
T2=rename(T2,c(variable="管理者水平",value="评分"))#这个语句要注意
#(1)方差分析
model1=aov(评分~管理者水平,data=T2)#注意这一项数值在前,类别变量在后
summary(model1)
#P=0.000633,因此有理由说明管理者水平对评分有影响
#计算效应量
library(DescTools)
EtaSq(model1,anova=T)
#结果表明评分总误差中被管理者水平解释的比例为62.54%
#(2)LSD,HSD方法比较管理者之间评分的差异,找出mu1,mu2,mu3之间到底哪两个均值不等,
#这种对均值的配对检验称之为方差分析中的多重比较。
library(agricolae)
LSD=LSD.test(model1,"管理者水平")
LSD
HSD=HSD.test(model1,"管理者水平")
HSD
#(3)正态性检验,QQ图,或者shapior-Wilk,K-S检验
qqnorm(T2$评分,xlab=c("观察值"),ylab=c("期望正态值"),main="QQ图")
qqline(T2$评分)
#shapiro检验正态性,P大于0.05则说明服从正态分布
shapiro.test(T2$评分)
#ks检验正态性
ks.test(T2$评分,"pnorm",mean(T2$评分),sd(T2$评分))
#方差齐性检验:画图,Bartlett方差齐性检验
plot(model1,which=c(1,2))
bartlett.test(评分~管理者水平,data=T2)
#也可以写成barlett(model1)
#P=0.3726>0.05表示不同管理者水平的评分满足方差齐性。
#8.5双因子方差分析
setwd("E:\\大三下学期\\R\\R_code\\data\\data\\")
T1<-read.csv(".\\exercise\\chap08\\exercise8_5.csv")
library(reshape)
T2=melt(T1,variable_name="路段")#将类别变量那一列进行命名
T2=rename(T2,c(value="车流量"))
#主效应方差分析
model2=aov(车流量~时段+路段,data=T2)
summary(model2)
#两个P值都小于0.05说明时段和路段对车流量有显著影响
#主效应方差分析的参数估计
model2$coefficients
#交互效应量分析
#设时段对车流量的影响效应为alpha1,alpha2,路段对车流量的影响效应为beta1,beta2,beta3,
#路段和时段对车流量影响的交互效应为gama_ij
#检验路段效应的假设为:H0:alpha1=alpha2=0,H1:alpha1,alpha2至少有一个不等于0
#检验时段效应的假设为:H0:bata1=beta2=beta3=0,H1:beta1,beta2,beta3至少有一个不等于0
#检验交互效应的假设为:H0:gama_ij=0(i=1,2,j=1,2,3),H1:gama_ij至少有一个不等于0
model3=aov(车流量~时段+路段+时段:路段,data=T2)
summary(model3)
#时段:路段的P值>0.05,说明时段和路段的交互效应不显著
#计算交互效应方差的效应量
library(DescTools)
EtaSq(model3)
#看第二列数据,在排除时段和路段交互影响后,时段对车流量的误差的解释比例为74.5%
#排除时段和路段交互影响后,路段解释了车流量误差的比例为64.7%
#排除路段和时段的影响后,路段和时段的交互效应解释了车流量误差的0.02%,
#如此小的偏效应量也证明了前面交互效应对车流量没有显著影响的结论
九、一元线性回归


#第九章
#线性回归建模的基本步骤
#1.检验变量之间的关系
#2.建立线性关系模型,并进行估计和检验
#3.用建立好的线性模型进行预测
#4.对模型进行诊断(包括正态性检验,ks,shapiro,plot和方差齐性检验ncvTest,plot(位置尺图))
setwd("E:\\大三下学期\\R\\R_code\\data\\data\\")
T1<-read.csv(".\\example\\chap09\\example9_1.csv")
#确定变量之间的关系
cor.test(T1$销售收入,T1$广告支出)
#p-value = 1.161e-09<0.05说明两个变量具有较强的线性相关性
model=lm(销售收入~广告支出,data=T1)
summary(model)
#看coefficients这一列的estimate参数,第一个为截距,第二个为斜率,
#同时第二行的t值和p_value反映了x对y的影响程度(回归系数检验)。
#这里p=1.16e-9表示广告支出是影响销售收入的重要因素
#Multiple R_Squared表示R2值(决定系数),越接近一则表示拟合效果越好,这里的决定系数R2=87.82%
#表示在销售收入取值的总误差中,有87.82%是可以由销售收入和广告支出之间的线性关系解释的
#输出方差分析表,用F检验,检验线性关系检验
anova(modle)
#结果里面有F值P值,P<0.05表示拒绝H0,即销售收入与广告支出之间的线性关系显著
#对新数据进行预测
x0=data.frame(广告支出=500)
predict(model,newdata=x0)
#求出均值置信区间:
predict(model,data.frame(广告支出=500),interval="confidence",level=0.95)
#求出预测区间:(预测区间大于置信区间)
predict(model,data.frame(广告支出=500),interval="prediction",level=0.95)
#模型的诊断:正态性检验,方差齐性检验
#正态性检验
ks.test(T1$广告支出,"pnorm",mean(T1$广告支出),sd(T1$广告支出))
shapiro.test(T1$广告支出)
#或者直接绘制模型的四个图看正态QQ图
plot(model1)
#方差齐性检验,在上面的四个图中的第三个(位置尺图)就可以看方差齐性,数据点在水平线周围随机分布
library(car)
ncvTest(model)#看P值是否大于0.05,大于则说明满足方差齐性

