博客

根据各行业特性，人们提出了多种聚类算法，简单分为：基于层次、划分、密度、图论、网格和模型的几大类。

其中，基于密度的聚类算法以DBSCAN最具有代表性。

场景 一

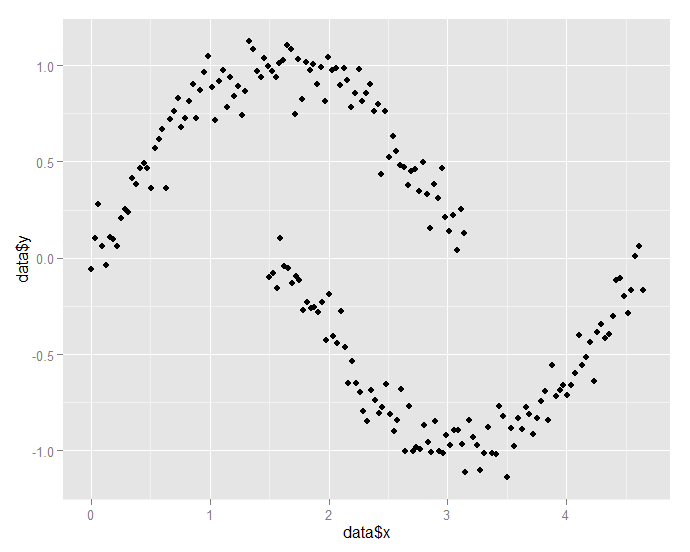
假设有如下图的一组数据， 生成数据的R代码如下

x1 <- seq(0,pi,length.out=100)
y1 <- sin(x1) + 0.1*rnorm(100)
x2 <- 1.5+ seq(0,pi,length.out=100)
y2 <- cos(x2) + 0.1*rnorm(100)
data <- data.frame(c(x1,x2),c(y1,y2))
names(data) <- c('x','y')    
qplot(data$x, data$y)
           

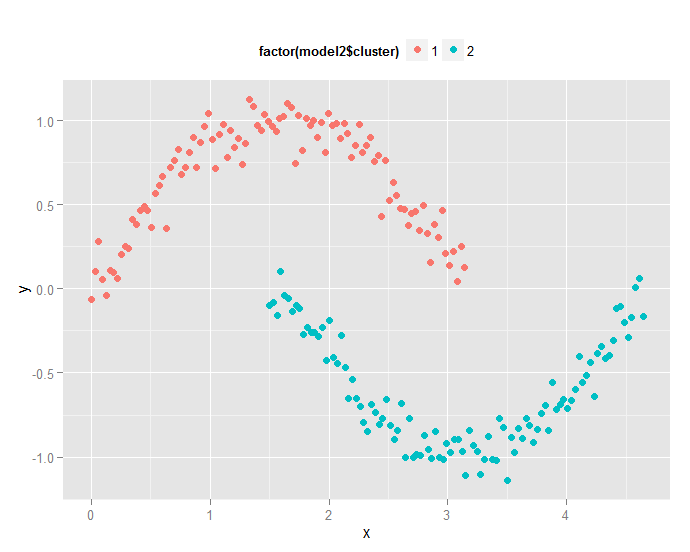
用密度聚类DBSCAN方法，可以看到聚类效果如下：

library(ggplot2)
p <- ggplot(data,aes(x,y))
library('fpc')
model2 <- dbscan(data,eps=0.6,MinPts=4)
p + geom_point(size=2.5, aes(colour=factor(model2$cluster)))+theme(legend.position='top')

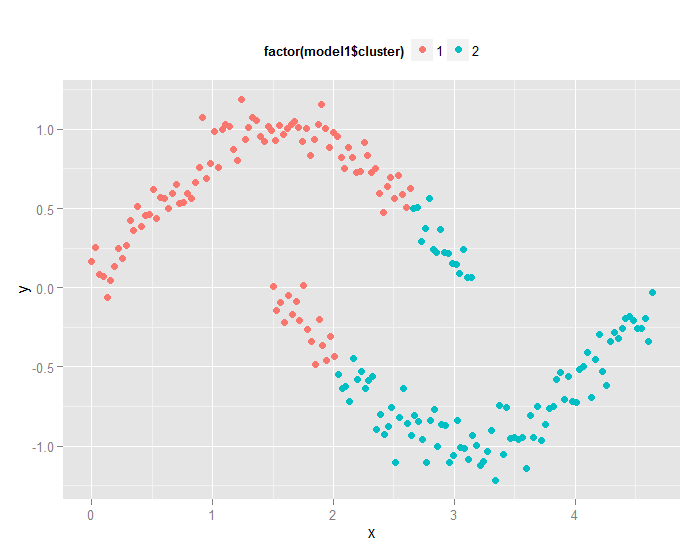
同样，请读者看下k-means的聚类效果。

# 用K均值聚类
model1 <- kmeans(data,centers=2,nstart=10)
library(ggplot2)
p <- ggplot(data,aes(x,y))
p + geom_point(size=2.5,aes(colour=factor(model1$cluster)))+theme(legend.position='top')

场景 二

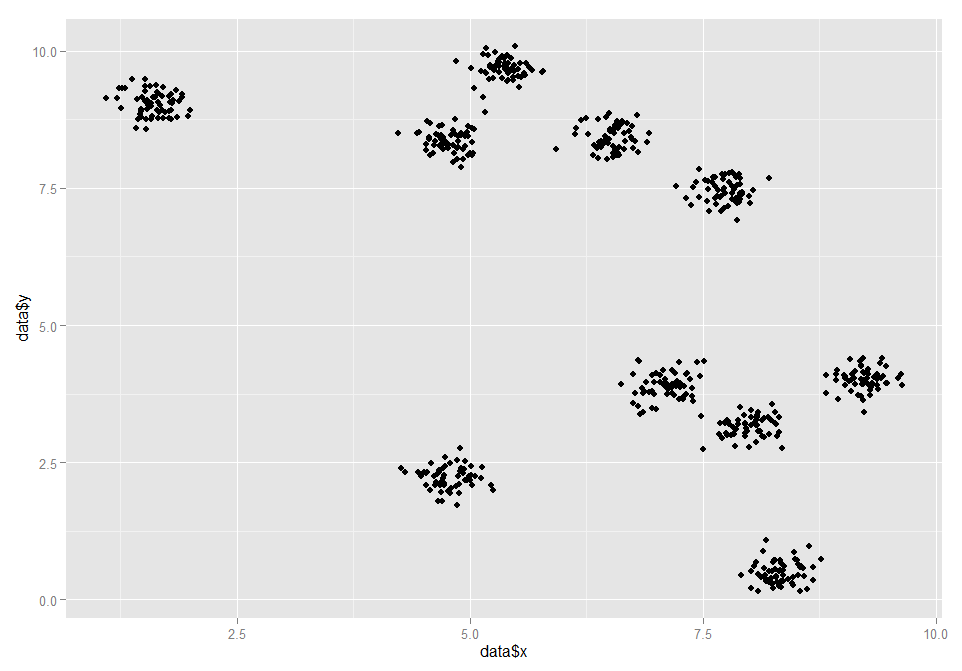
假设有如下一组数据，生成数据的R代码如下。

set.seed(665544)
n <- 600
data <- data.frame(cbind(runif(10, 0, 10)+rnorm(n, sd=0.2), runif(10, 0, 10)+rnorm(n,sd=0.2)))
names(data) <- c('x','y')
library(ggplot2)
qplot(data$x, data$y)

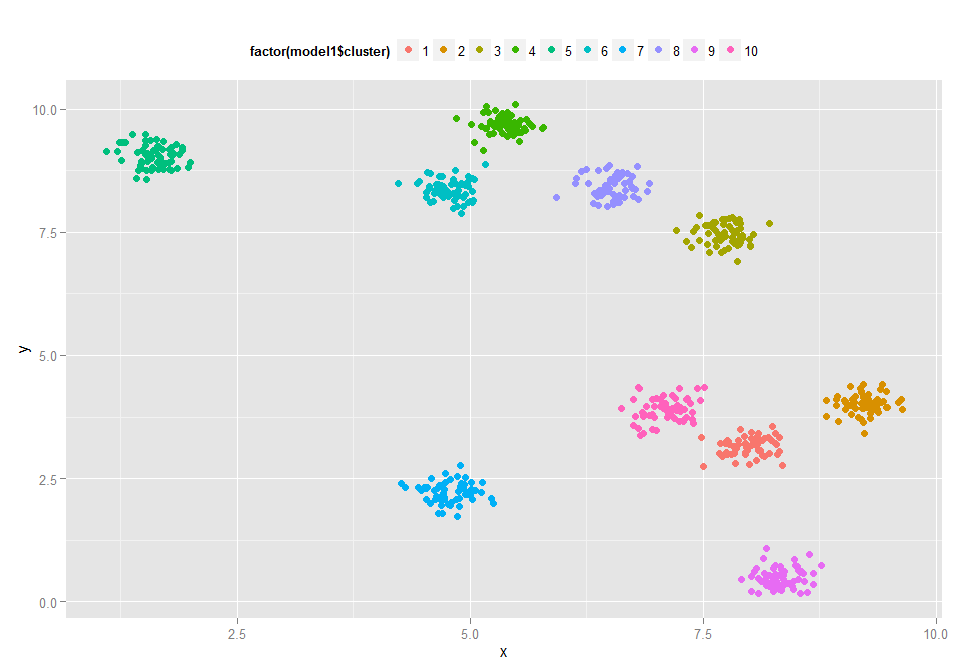
笔者用k-means聚类效果如下

# 用K均值聚类
model1 <- kmeans(data,centers=10,nstart=10)
library(ggplot2)
p <- ggplot(data,aes(x,y))
p + geom_point(size=2.5,aes(colour=factor(model1$cluster)))+theme(legend.position='top')

用dbscan算法聚类效果如下。

#用dbscan聚类
p <- ggplot(data,aes(x,y))
library('fpc')
model2 <- dbscan(data,eps=0.2,MinPts=5)
p + geom_point(size=2.5, aes(colour=factor(model2$cluster)))+theme(legend.position='top')

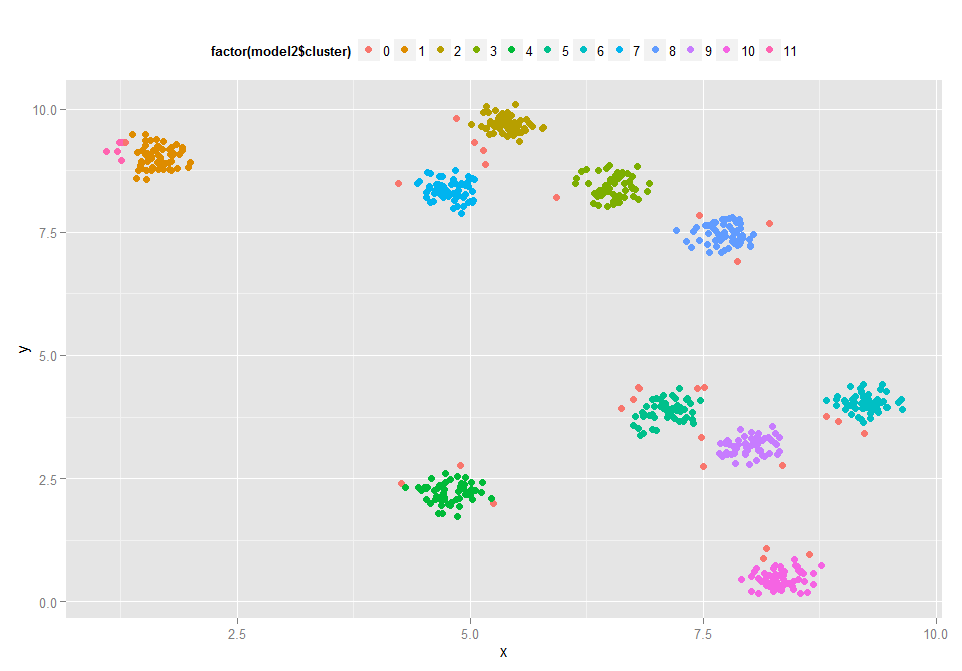
请注意观察两个算法的不同之处。

1 dbscan是基于密度计算聚类的，会剔除异常（噪声点）。如上图中的类别0，就是dbscan算法聚类出的噪声点（不是核心点且不再核心点的邻域内）。

2 k-means需要指定k值，并且初始聚类中心对聚类结果影响很大。

3 k-means把任何点都归到了某一个类，对异常点比较敏感。

其它的观点。来自《数据挖掘导论》[美]Pang-Ning Tan,Michael Steinbach,Vipin Kumar 著 page355-356

为了简化比较，我们假定对于K均值和DBSCAN都没有距离的限制，并且DBSCAN总是将与若干个核心点相关联的边界点指派到最近的核心点。

1. K均值和DBSCAN都是将每个对象指派到单个簇的划分聚类算法，但是K均值一般聚类所有对象，而DBSCAN丢弃被它识别为噪声的对象。

2. K均值使用簇的基于原型的概念，而DBSCAN使用基于密度的概念。

3. K均值很难处理非球形的簇和不同大小的簇。DBSCAN可以处理不同大小或形状的簇，并且不太受噪声和离群点的影响。当簇具有很不相同的密度时，两种算法的性能都很差。

4. K均值只能用于具有明确定义的质心（比如均值或中位数）的数据。DBSCAN要求密度定义（基于传统的欧几里得密度概念）对于数据是有意义的。

5. K均值可以用于稀疏的高维数据，如文档数据。DBSCAN通常在这类数据上的性能很差，因为对于高维数据，传统的欧几里得密度定义不能很好处理它们。

6. K均值和DBSCAN的最初版本都是针对欧几里得数据设计的，但是它们都被扩展，以便处理其他类型的数据。

7. 基本K均值算法等价于一种统计聚类方法（混合模型），假定所有的簇都来自球形高斯分布，具有不同的均值，但具有相同的协方差矩阵。DBSCAN不对数据的分布做任何假定。

8. K均值DBSCAN和都寻找使用所有属性的簇，即它们都不寻找可能只涉及某个属性子集的簇。

9. K均值可以发现不是明显分离的簇，即便簇有重叠也可以发现，但是DBSCAN会合并有重叠的簇。

10. K均值算法的时间复杂度是O(m)，而DBSCAN的时间复杂度是O(m^2)，除非用于诸如低维欧几里得数据这样的特殊情况。

11. DBSCAN多次运行产生相同的结果，而K均值通常使用随机初始化质心，不会产生相同的结果。

12. DBSCAN自动地确定簇个数，对于K均值，簇个数需要作为参数指定。然而，DBSCAN必须指定另外两个参数：Eps（邻域半径）和MinPts（最少点数）。

13. K均值聚类可以看作优化问题，即最小化每个点到最近质心的误差平方和，并且可以看作一种统计聚类（混合模型）的特例。DBSCAN不基于任何形式化模型。

所以，不同的数据集和场景，需要运用不同的聚类算法。

下面介绍该算法的工作原理。

其中，DBSCAN方法对参数eps和

MinPts敏感。

在这个算法框架中，NEps(x, D)表示数据集D中包含在对象x的Eps-邻域范围内的

所有子对象。card(N)表示集合N的基数，即集合N中包含的元素的个数。在簇扩展

过程中采用了栈结构，用于压栈当前对象x的所有邻居对象，再递归地判断栈成员

是否满足核心对象条件，从而决定是否进一步扩展。

后记：

1 关于算法的一般性介绍，可参看百度百科介绍。

http://baike.baidu.com/link?url=cnLtGJsF_a4CzmVbAev3nFH75nZUMgwClKv_kk2ZsXuXrP1gvY8eMvY75UDL29AMJFJ2n60xB680PMkjitrG4a

2 按照上述的算法流程，作者写了java代码放入了百度云盘（含上述测试数据），有兴趣的读者请自行下载。

http://pan.baidu.com/s/1ntwyXkP

3 参考文献 《针对非均匀数据集的DBSCAN聚类算法研究》 重庆大学硕士学位论文   陈若田   二O 一三年四月

http://pan.baidu.com/s/1mgvKR7U

4 Clustering

http://scikit-learn.org/stable/modules/clustering.html#spectral-clustering

5 python DBSCAN源码

http://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html#example-cluster-plot-dbscan-py

（完）