博客

文章来源：

http://www.codelast.com/

如果你关心最优化（Optimization），你一定听说过一类叫作“信赖域（Trust Region）”的算法。在本文中，我将讲述一下信赖域算法与一维搜索的区别、联系，以及信赖域算法的数学思想，实现过程。

【1】信赖域算法与一维搜索算法的区别、联系

最优化的目标是找到极小值点，在这个过程中，我们需要从一个初始点开始，先确定一个搜索方向 d ，在这个方向上作一维搜索（line search），找到此方向上的可接受点（例如，按两个准则的判定）之后，通过一定的策略调整搜索方向，然后继续在新的方向上进行一维搜索，依此类推，直到我们认为目标函数已经收敛到了极小值点。

这种通过不断调整搜索方向，再在搜索方向上进行一维搜索的技术被很多很多算法采用，也取得了很实际的工程意义，但是，我们非要这样做不可吗？有没有另外一种途径，可以不通过“调整搜索方向→进行一维搜索”的步骤，也能求得极小值点？当然有，这就是信赖域算法干的好事。

为了说明这两种途径所实现的算法的区别和联系，请允许我做一个可能不太恰当，但是比较形象的比喻：

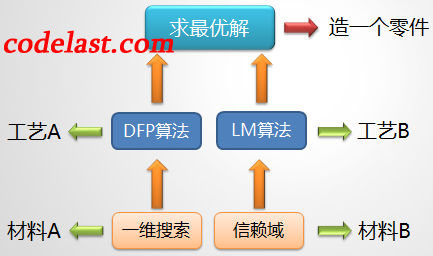
上图表述的是：如果把求最优解的过程比喻为“造一个零件”的过程的话，那么，使用一维搜索的那些算法和信赖域算法就像是两种不同的工艺，它们分别使用不同的技术（一维搜索&信赖域方法）——即两种不同的材料作为达成最终目标的基础。

作为一个了解最优化理论并不多的人，我从我看到过的书得到的感受就是：相比使用一维搜索的那一类算法，貌似信赖域算法们的应用还不够那么多。当然这仅仅是个人感觉，勿扔砖…

【2】信赖域算法的基本思想

信赖域和line search同为最优化算法的基础算法，但是，从“Trust Region”这个名字你就可以看出，它是没有line search过程的，它是直接在一个region中“search”。

在一维搜索中，从 xk 点移动到下一个点的过程，可以描述为： xk+αkdk

此处 αkdk 就是在 dk 方向上的位移，可以记为 sk

而信赖域算法是根据一定的原则，直接确定位移 sk ，同时，与一维搜索不同的是，它并没有先确定搜索方向 dk 。如果根据“某种原则”确定的位移能使目标函数值充分下降，则扩大信赖域；若不能使目标函数值充分下降，则缩小信赖域。如此迭代下去，直到收敛。

关于这种寻优的方法，我这里又有一个比喻，希望能帮助你理解：

要从上海火车站去人民广场，有两种方法：

①可以先定一个方向，比如先向西走，走着走着发现方向有点不对（人民广场应该是时尚地标啊，怎么越走感觉越郊区了呢），就调整一下方向，变成向东南方向走，诸如此类。

②用信赖域算法，就比如，我先划一个圈，然后在这个圈里面找离人民广场可能最接近的点，如果我的圈划得太大了，一下子就划到了莘庄（不熟悉上海的同学可以查一下地图），我一步就走到了上海南站，那还得了，马上给我回来，把圈缩小到两个地铁站的距离之内，然后再在里面找离人民广场最近的点。

【3】信赖域算法的数学模型

前面说了，根据一定的原则，可以直接确定位移，那么，这个原则是什么呢？

答：利用二次模型模拟目标函数 f(x) ，再用二次模型计算出位移 s 。根据位移 s 可以确定下一点 x+s ，从而可以计算出目标函数的下降量（下降是最优化的目标），再根据下降量来决定扩大信赖域或缩小信赖域。

那么，我该如何判定要扩大还是缩小信赖域呢？为了说明这个问题，必须先描述信赖域算法的数学模型：

$$min q^k(s) = f(x_k) + g_k^Ts+\frac{1}{2}s^TG_ks \\ s.t. ||s||\leq h_k$$

第一个式子就是我们用于模拟目标函数的二次模型，其自变量为 s ，也就是我们要求的位移。 gk 为梯度， Gk 为Hesse矩阵，袁亚湘的书上说，如果Hesse矩阵不好计算，可以利用“有限差分”来近似 Gk （不好意思我不懂），或者用拟牛顿方法来构造Hesse矩阵的近似矩阵。

第二个式子中的 hk 是第 k 次迭代的信赖域上界（或称为信赖域半径），因此第二个式子表示的就是位移要在信赖域上界范围内。此外，第二个式子中的范数是没有指定是什么范数的，例如，是2-范数还是∞-范数之类的（在实际中都有算法用这些范数）。

现在又回到了上面的问题：我该如何判定要扩大还是缩小信赖域呢？通过衡量二次模型与目标函数的近似程度，可以作出判定：

第 k 次迭代的实际下降量为：










Δ




f




k


=


f




k


−


f




(


x


k


+


s


k


)










$Δfk=fk−f(xk+sk)$

第 k 次迭代的预测下降量为：










Δ




m


k


=


f




k


−


m


(


s


k


)










$Δmk=fk−m(sk)$

定义比值：








r


k


=




Δ




f




k




Δ




m


k










$rk=ΔfkΔmk$

这个比值可以用于衡量二次模型与目标函数的近似程度，显然 r 值越接近1越好。

由此，我们就可以给出一个简单的信赖域算法了。

【4】信赖域算法的步骤

一个考虑周全的信赖域算法可能非常麻烦，为了说明其步骤，这里只说明基本的迭代步骤：

从初始点 x0 ，初始信赖域半径 h0=∥g0∥ 开始迭代

到第 k 步时，计算 gk 和 Gk

解信赖域模型，求出位移 sk ，计算 rk

若 rk≤0.25 ，说明步子迈得太大了，应缩小信赖域半径，令 hk+1=∥sk∥4

若 rk≥0.75 且 ∥sk∥=hk ，说明这一步已经迈到了信赖域半径的边缘，并且步子有点小，可以尝试扩大信赖域半径，令 hk+1=2hk

若








0.25


<


r


k


<


0.75










$0.25<rk<0.75$
，说明这一步迈出去之后，处于“可信赖”和“不可信赖”之间，可以维持当前的信赖域半径，令 hk+1=hk,若 rk≤0 ，说明函数值是向着上升而非下降的趋势变化了（与最优化的目标相反），这说明这一步迈得错得“离谱”了，这时不应该走到下一点，而应“原地踏步”，即 xk+1=xk ，并且和上面 rk≤0.25 的情况一样缩小信赖域。反之，在 rk>0 的情况下，都可以走到下一点，即 xk+1=xk+sk

【5】最重要的一种信赖域算法：Levenberg-Marquardt算法

当信赖域模型中的范数 ∥s∥≤hk 取2-范数时（即 ∥s∥2≤hk ），就得到了Levenberg-Marquardt算法（简称LM算法）的数学模型：

$$min q^k(s) = f(x_k) + g_k^Ts+\frac{1}{2}s^TG_ks \\ s.t. ||s||\leq h_k$$

具体请看LM算法。

【6】信赖域算法的收敛性

信赖域算法具有整体收敛性。这个证明略。