所有用公式写的式子以前都好好的,但是突然都显示得不太对了!先不改了有时间再改。
知识总结:


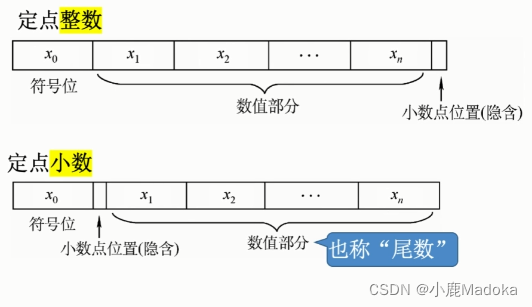
2.2.1 定点数的表示
定点数:
小数点的位置固定;
浮点数:
小数点的位置不固定(加科学计数法的阶码);

一、无符号数
无符号数:
整个机器字长的全部二进制位均为数值位,没有符号位(+、-),相当于数的绝对值。
(通常只有
无符号整数unsigned int
、unsigned long,而没有无符号小数)
以下算式中,
数后面加B表示这个数是二进制数,加D表示十进制数
1001 1100B

表示范围:
8位二进制数:
种不同的状态 0000 0000 ~ 1111 1111,转换成十进制数值就是0 ~ 255,最大值是
;
n位的无符号数表示范围为:0~
二、有符号数的定点表示
可用
原码、反码、补码
三种方式来表示定点整数和定点小数。还可用
移码
表示定点整数。
若真值为x,则用
![]()
分别表示真值所对应的原码、反码、补码、移码。
1.原码
原码:
用尾数表示真值的绝对值,符号位 “0/1” 对应 “正/负”
定点整数:
若机器字长n+1位,
原码整数
的表示范围:
(关于原点对称)
真值0有
+0和-0
两种形式
19 = 16 + 2 + 1 机器字长8位时,常写为:[x]原 = 1,0010011(
隔开的是逗号
),若未指名机器字长,也可写为:[x]原 = 1,10011
| 符号 |
|
|
|
|
|
|
|
|
| +19D | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| -19D | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
尾数的位权(2的几次方)取决于小数点的位置。
定点小数:
若机器字长n+1位,
原码小数
的表示范围:
(关于原点对称)
真值0有
+0和-0
两种形式
0.75 = 0.5 + 0.25 常写为:[x]原 = 1.1100000(
隔开的是小数点
)
| 符号 |
|
|
|
|
|
|
|
|
| +0.75D | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| -0.75D | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
2.反码
反码:
若符号位为0,则反码与原码相同;
若符号位为1,则数值位全部取反。

若机器字长n+1位,
反码整数
的表示范围:
(关于原点对称)
真值0有
+0和-0
两种形式
若机器字长n+1位,
反码小数
的表示范围:
(关于原点对称)
真值0有
+0和-0
两种形式
“反码”只是“原码”转变为“补码”的一个中间状态,实际中并没有什么用。
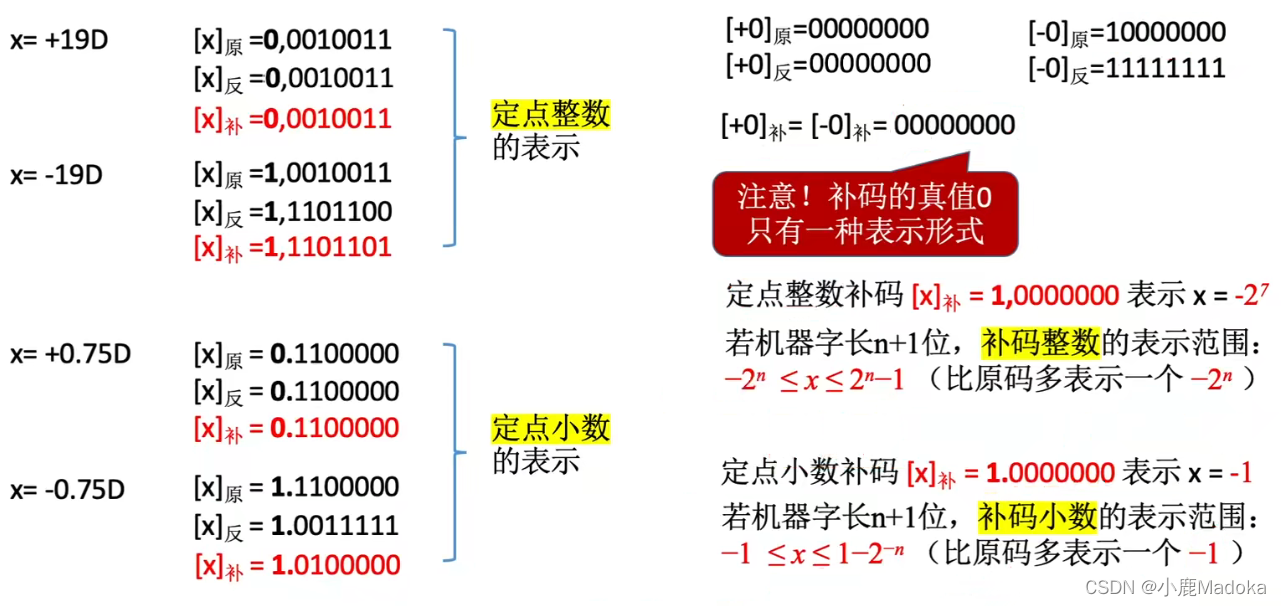
3.补码
正数的补码 = 原码
负数的补码 = 反码末位 + 1 (要考虑进位)
将负数补码转回原码:尾数取反,末位+1
(x取反
→
反码:-x,加一 → 补码:-x+1, 再取反 → x-1,加一 → 原码:x)
4.移码
补码的基础上符号位取反。(移码只能用于表示整数)
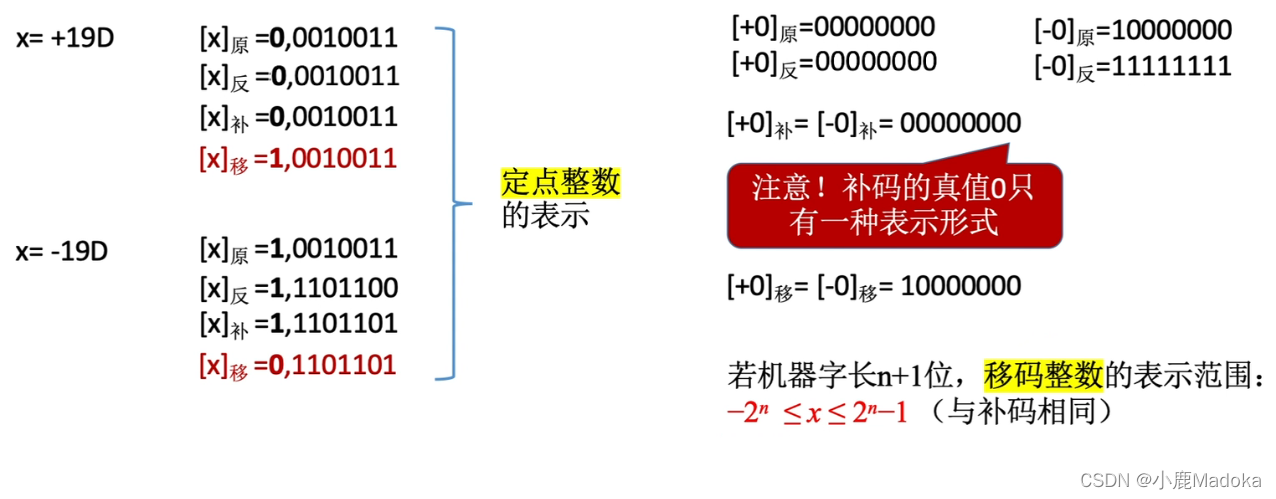
把移码看成无符号数,就会发现它是一直递增的。

5.用几种码表示定点整数
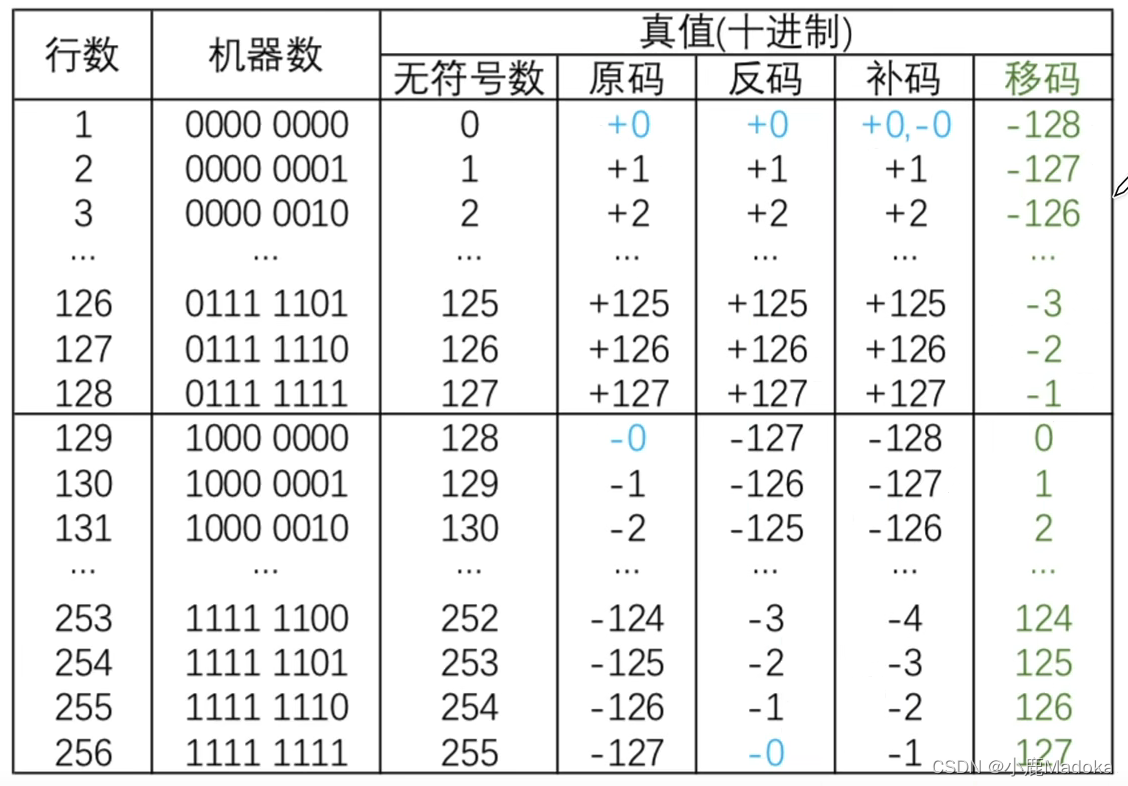
原码和反码的真值0有两种表示(正0和负0),
补码和移码的真值0只有一种表示,补码和移码可以多表示一个负数。
定点数整数:
正数的原码,反码,补码都和原码是一样的,移码是符号位取反;
负数的反码是除符号位全取反,补码是反码+1,移码是符号位取反;
做原、反、补、移码转换对应真值时,记得算出来结果后一定要检查符号,看负号是否漏加了。
技巧:由 [x]补 快速求 [-x]补 的方法——符号位、数值位全部取反,末位+1