博客

机器学习20_线性判别分析（LDA）详解（2021.07.07）

一. 究极总结：

投影后类内方差最小，类间方差最大。

二. 知识理解

1. LDA的思想非常朴素，给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。在对新样本进行分类时，将其投影到同样的这条直线上，在根据投影点的位置来确定新样本的类别。如下图所示：
   
   
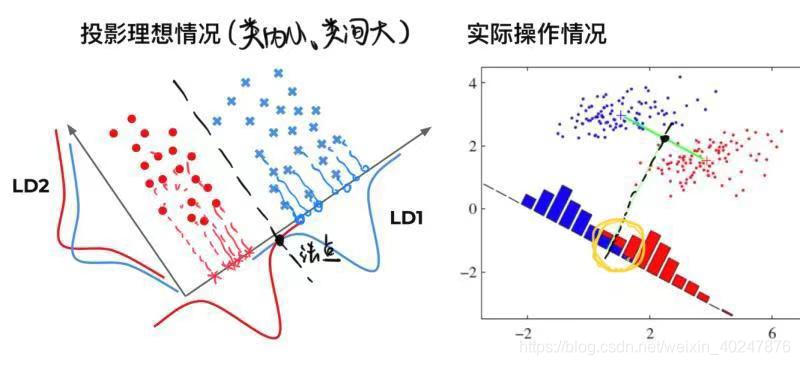
2. 在将所有的点通过降维的思想投影到直线上之后，实现了所谓的同类样例接近，异类样例远离的结果。如图中左边的理想情况，甚至可以找到一个法点以及它的法线，从而清晰地将两个不同类别的样例区分开来。但更一般的情况下，如图中右边的情况，是很难找到这个法点的，因此我们需要探究以下如何在一般情况下找到那个法点。
3. 其实找到这个法点并不难，只要我们绘制出投影结果的分布概率图就可以了。如下所示：
   
   
   
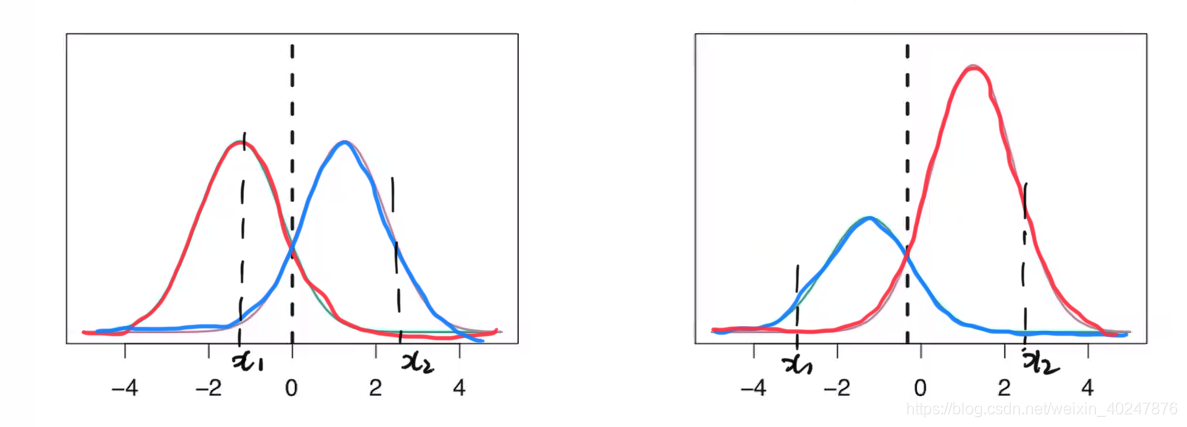
   如上图所示，蓝色曲线代表一个类别，红色曲线代表另一个类别，当有一个未知的点x1想要进行分类的预测时，其在概率分布图中的对应红色曲线和蓝色曲线的值就决定了它的分类情况，如左图中的x1点，明显其在红色曲线上的概率明显大于蓝色曲线的，因此就被分为了红色曲线一类。曲线在各个点的高度代表着这个范围内分布数据的多少。而两条曲线之间的交点就可以被看做是那个法点（阈值）。

三. 红酒品质数据集的LDA降维代码实现

import pandas as pd
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
import matplotlib.pyplot as plt

# 读取红酒数据集
df = pd.read_csv('winequality-red.csv', sep=';')
print(df)

# 切分数据集
X = df.drop('quality', axis=1)
y = df.quality

lda = LDA(n_components=2)  # 将原来11维的数据降维成二维
dataMat_new = lda.fit_transform(X, y)

# 打印降维的结果
print(X.shape)  # (1599, 11)
print(dataMat_new.shape)  # (1599, 2) 可见从11维降到了

# 绘制降维后的点图
plt.scatter(dataMat_new[:, 0], dataMat_new[:, 1])
plt.show()

四. 结果展示

五. 感悟与分享

1. LDA降维与PCA降维的区别在于：PCA是不考虑样本类别输出的无监督降维技术，LDA是一种监督学习的降维技术。
2. 红酒品质数据集博主上传到了网盘，需要的朋友请自取：
   
   链接在此
   
   提取码：demo

如有问题，敬请指正。欢迎转载，但请注明出处。