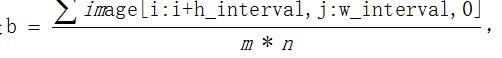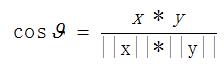本次主要对比三种分类算法的效果
1、
基于余弦相似度
2、
基于线性
svm
3、
基于
softmaxregression
因为目前还没有学习
deep learning
之类,如
cnn
可以直接处理行图像(如
200*200
的
image ->1*40000
)
,
但是深度学习要求大量的数据才能成功。本次实验数据从该网址
:
http://www.robots.ox.ac.uk/~vgg/data/flowers/
下载,选取了三种花,每种花有三个样本。因为数据少,所以要自己提取一些有用的信息。
第一步:提取图像特征
1
)首先将读入的图像均缩放为
400*200
的图像
2
)将图像划分为
m(
行
)*n(
列
)—
本次实验是
5*10
,对其分块,每一块大为
80*20
。
3
)遍历图像三个通道,每一块取其均值作为最后的值。
即是
,
g,r
通道同理
4
)最后的特征大小为
50*3[b,g,r],
将其转置
->3*50
第二步:确定训练集合训练集
label
1)
遍历每个类别文件夹下的图像,利用步骤一得到训练集。因为本次类别个数为
3
,每个类别下有三个图像。所以样本总数为
9
,因为步骤一提取每个图像的特征码大小为
3*50
,因此要将其拉伸变为
1*150
。故训练集大小为
9*150
。
2)
Label
大小
9*1
第三步
:
分类
法
1
:利用余弦相似度
原理简单粗暴。
取相似度最大的类别作为最终的分类结果。
法
2
:利用
SVM
,因为特征数目大于样本数目,所以使用线性
svm– LinearSVC()
法
3
:利用
softmax regression
,
softmax
是二元逻辑回归的推广。对于
softmax,
只能用在相互独立的类别上,如不同类型的植物,它不能识别同一张照片上不同的人。
代码如下:
# -*- coding: utf-8 -*-
import cv2
import numpy as np
import os
#import mlpy
from PIL import Image,ImageDraw,ImageFont
from sklearn.svm import LinearSVC
from sklearn.linear_model import LogisticRegression
def getfeature(filename,m,n):
fimage=cv2.imread(os.path.abspath(filename))
fimage=cv2.resize(fimage,(400,200))#(宽,高)
h,w=fimage.shape[0],fimage.shape[1]
h_interval=int(h/m)
w_interval=int(w/n)
allxyz=[]
for i in range(0,h,h_interval):
for j in range(0,w,w_interval):
b=fimage[i:i+h_interval,j:j+w_interval,0]
g=fimage[i:i+h_interval,j:j+w_interval,1]
r=fimage[i:i+h_interval,j:j+w_interval,2]
btz=np.mean(b)
gtz=np.mean(g)
rtz=np.mean(r)
allxyz.append([btz,gtz,rtz])
# allxyz=np.array(allxyz).T
# pca=mlpy.PCA()
# pca.learn(allxyz)
# allxyz=pca.transform(allxyz,k=len(allxyz)/2)
# pca_allxzy=pca(allxyz,int((m*n)/2))
# print(pca_allxzy.shape)
# return pca_allxzy.T
# return np.array(allxyz)
return np.transpose(np.array(allxyz))
def compute_cosin(x,y):
if isinstance(x,list) or isinstance(y,list):
x=np.array(x)
y=np.array(y)
return np.dot(x,y)/(np.linalg.norm(x)*np.linalg.norm(y))
def test_image(filename_image,train_x, y_label_train):
xyz=getfeature(filename_image,m,n)
xyz=xyz[0].tolist()+xyz[1].tolist()+xyz[2].tolist()
similar=[]
for i in range(len(y_label_train)):
similar.append(compute_cosin(train_x[i],xyz))
index=np.argsort(-np.array(similar))[0]
print(similar)
print(".jpg属于第%s"%( y_label_train[index]))
def pca(x,k):
x=x.T
x_mean=x-np.mean(x,0)
con_x=np.cov(x_mean)
evar,evas=np.linalg.eig(con_x)
new_x=np.dot(evas[:,:k].T,x)
return new_x.T
def cv_imageto_image(image,classname):
w=image.shape[1]
pil_im=Image.fromarray(image)
ttfont =ImageFont.truetype(r"C:\Windows\Fonts/STXIHEI.ttf",20)
draw = ImageDraw.Draw(pil_im)
draw.text((w/2,10),u'%s'%classname, fill=(255,255,0),font=ttfont)
cv_im=cv2.cvtColor(np.array(pil_im),cv2.COLOR_RGB2RGBA)
return cv_im
if __name__=="__main__":
### 类别特征码,训练样本#######
m,n=5,10 #区域大小
pic_class=3
train_x=[]
y_label_train=[u"黄花",u"黄花",u"黄花",u"白花",u"白花",u"白花",u"向日葵",u"向日葵",u"向日葵"]
for c in range(1,pic_class+1):
# txyz=np.zeros((3,m*n))
for i in range(1,4):#每个类别3个样本图像
fn="C:\\Users\\Y\\Desktop\\demo\\"+str(c)+"\\"+str(i)+".jpg"
# temp_xyz=getfeature(fn,m,n)
txyz=getfeature(fn,m,n)
# txyz+=temp_xyz#各类别图像特征码之和
# y_label_train.append(c)
# txyz=txyz/3#均值
train_x.append(txyz[0].tolist()+txyz[1].tolist()+txyz[2].tolist())
train_x=np.array(train_x)
y_label_train=np.array(y_label_train).T
#######测试#################
f1="C:\\Users\\Y\\Desktop\\demo\\6.jpg"
test_im=cv2.imread(f1)
test_image(f1,train_x,y_label_train)
# svm=mlpy.LibSvm()
# svm.learn(train_x,y_label_train)
##########svm 分类###############
xyz=getfeature(f1,m,n)
xyz=xyz[0].tolist()+xyz[1].tolist()+xyz[2].tolist()
xyz=np.array(xyz)
clf = LinearSVC() #svc()的话就错了,需要线性svc
clf.fit(train_x, y_label_train)
print("svm分类效果:属于第%s"%(clf.predict([xyz.T])[0]))
test_im=cv_imageto_image(test_im,clf.predict([xyz.T])[0])
softmax_reg=LogisticRegression(multi_class="multinomial",solver="lbfgs",C=10)
softmax_reg.fit(train_x, y_label_train)
print(softmax_reg.predict([xyz.T])[0])
cv2.imshow("test_im",test_im),cv2.waitKey(0)
# print(svm.pred(xyz))
法1、余弦分类效果:
属于黄花
法2、svm分类效果:属于黄花
法3:softmax 分类效果:属于黄花
test 2_image

法1、余弦分类效果:
属于黄花
法2、svm分类效果:属于白花
法3:softmax 分类效果:属于白花
可以看出来,法1错误分类,在样本量少的情况下,svm和softmax分类最佳。