数据的概括性度量
数据分布的特征有三个方面的测度和描述
1、分布的集中趋势:反映各数据向其中心值靠拢或者聚集的程度
2、分布的离散程度:反映各数据远离其中心值的趋势
3、分布的形状,反映数据分布的偏态和峰态
集中趋势的度量
疑惑点:低层次数据集中趋势测度值适用于高层次的测量数据;反过来,高层次数据的集中趋势测度值并不适用于低层次的测量数据。
分类数据,众数:是一组数据中出现次数最多的变量值
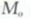
表示。
作用是:测量分类数据的集中趋势,也可以做为顺序数据以及数值型数据集中趋势的测量度。一般情况下,只有在数据量较大的情况下,众数才有意义。
在Excel中函数是:MODE(…
)
以下是众数的示意图
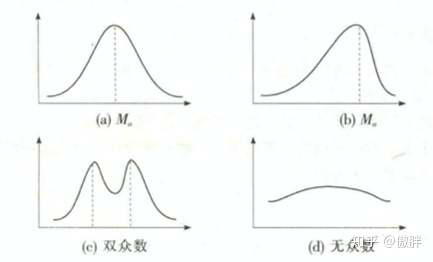
顺序数据,中位数和分位数:包括四分位、十分位、百分位数等
中位数(median)是一组数据排序后处于中间位置上的变量,用
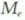
表示。
四分位数、十分位(decile)、百分位(percentile) 分别是用3个点、9个点、99个点将数据4等分、10等分、100等分后各分位点上的值。
Excel函数计算公式:
中位数:MEDIAN(…)
四分位数:QUARTILE(【选定的数组】, quart(参数) ) 。参数=0:返回最小值;参数=1:返回第一个四分位数;参数=2:返回中位数;参数=3:返回第三个四分位数;参数=4:返回最大值
其他分位数:PERCENTILE(【选定的数组】,百分值) 。
公式展示
中位数:
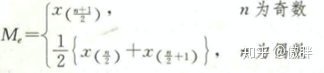
当数组为奇数时会得出唯一值,这个就为中位数;如果为偶数时会得出XX.5的数值,则选择该值的位置上的(前一个数值+后一个数值)/ 2 得出中位数。
四分位数的,上四分位数和下四分位数的位置求解公式:
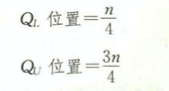
具体数值的求解案例:
例如:1,2,3,4,5,6,7,8,9
QL(位置)=9/4=2.25
QL(值)=2+(3-2)*0.25=2.25
QU(位置)=3*9/4=6.75
QL(值)=6+(7-6)*0.75=6.75
数值型数据:平均数
简单平均数:未经分组数据计算的平均数。就是其实就是 “ 平均数=(n个数值相加)/ n ”
加权平均数:根据分组数据计算的平均数。设原始数据分为k组,各组的组中值分别
M1,M2,…Mk,
各组变量值出现的频数(就是出现的次数)分别为
f1,f2,…,fk,
所以加权平均数的计算公式为
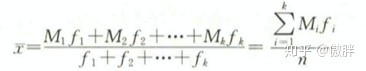
Excel函数计算公式
语法:AVERAGE(….)
一种特殊的平均数:几何平均数
几何平均数(geometric mean) 是 n 个变量成绩的 n 次方根,用 G 表示。它主要用于计算平均比率,比如说:平均增长率。

Excel函数计算公式
语法:GEOMEAN(…)
平均收益率的计算公式
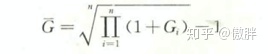
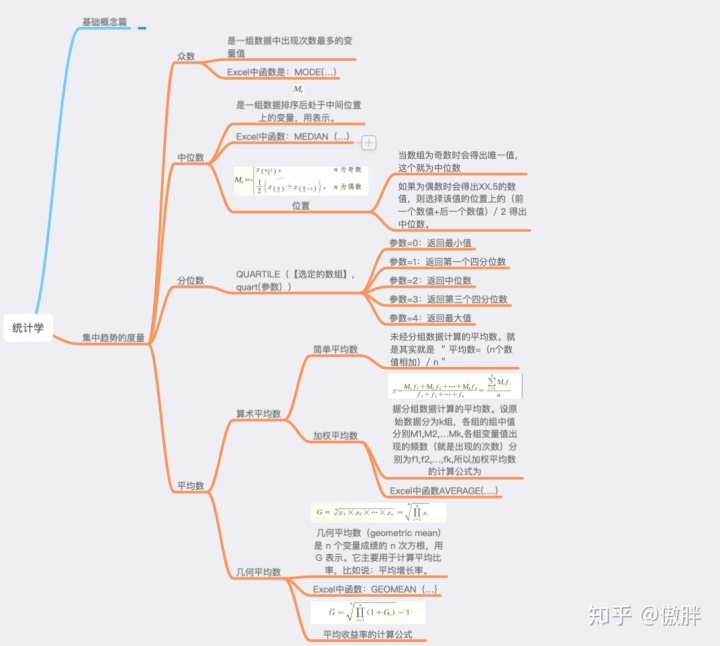
本篇内容脑图如下: