拓扑排序和关键路径都是有向无环图的重要应用

拓扑排序

拓扑排序的定义就是从一个集合的偏序关系得到该集合的全序关系。从离散数学中我们可知，假如R是集合X上的偏序关系，则R是自反，反对称和传递的。而全序关系是具有偏序关系特性的同时，对每个

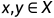
都有

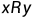
或者

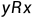
（但是由于反对称，

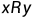
和

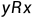
不能同时满足)。

在偏序关系的有向图中加上某些弧成为全序关系，则这个全序关系称为

拓扑有序

。

用一个偏序的有向图来表示一个流程图，其中顶点表示活动，边则表示的先决条件，也就是活动的优先级，这叫做

AOV网（Activity On Vetex Network）

。例如学完《离散数学》和《程序设计基础》才能学习《数据结构》，所以用AOV网来表示，如下

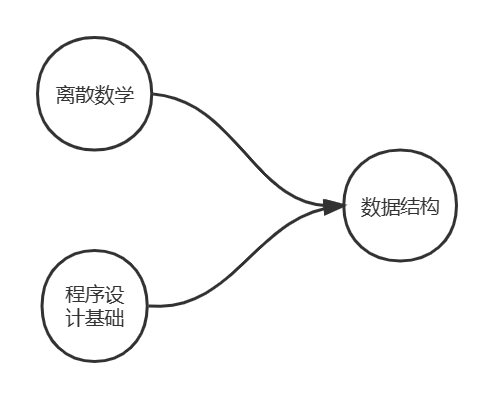
在AOV网不能出现有向环，因为一个活动的优先级高于它本身的优先级是矛盾的。对一个AOV网判定是否出现这种矛盾，其办法便是拓扑排序，若所有顶点都在这个序列当中，则该AOV网不会存在有向环（假如存在环，则一定有入度不为零的点）。

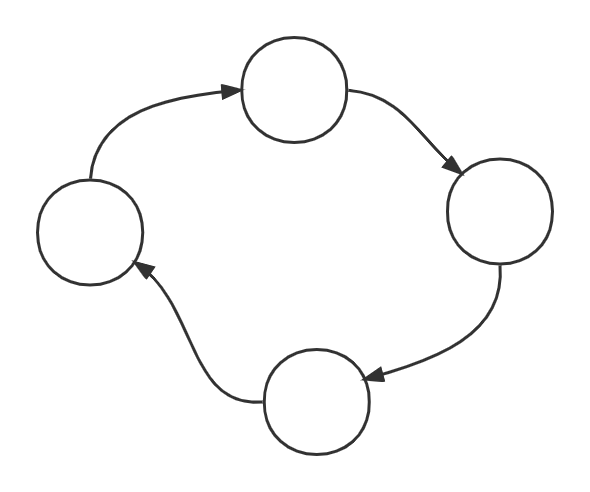
进行拓扑排序的方法为：在图中选择一个没有前驱的顶点删除并将该顶点加入序列（同时删除以该顶点为尾的弧），直到图中没有入度为0的顶点为止。如以下步骤

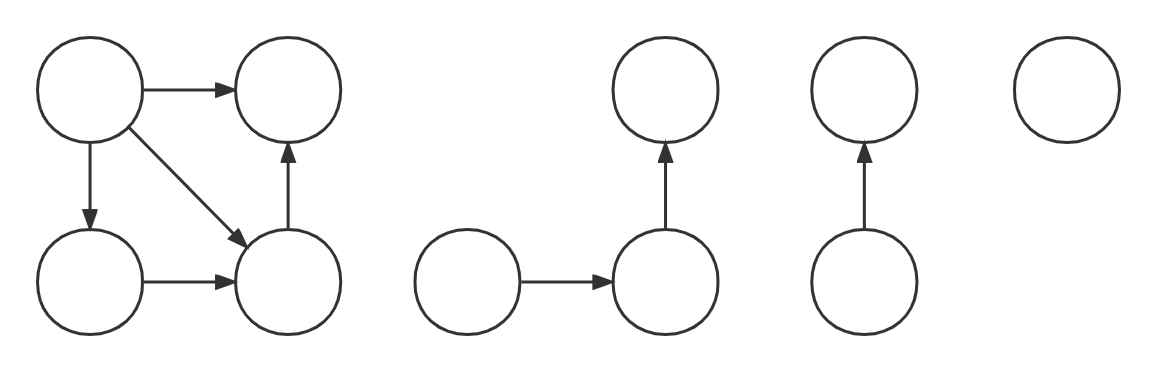
我们用邻接表实现拓扑排序判端是否有环的算法，只需在顶点数组里加入入度的数组，每一步删除入度为0的顶点，并且通过以该点为尾的弧找到以该弧为头的顶点，每个这样的顶点入度都减一，入度为0的顶点通过以栈的形式保存，能避免入度为0的顶点重复检测。

bool TopologicalSort(AlGraph G)
{
    int* stk = (int*)malloc(sizeof(int) * G.vexnum);//用栈来保存入度为0的顶点
    int i = 0;
    for (int v = 0; v < G.vexnum; v++)
    {
        if (!G.vertices[v].indgree)stk[i++] = v;
    }//入度为0的顶点入栈
    int count = 0;//通过计数来判断是否所有顶点都加入拓扑有序序列
    int temp;
    while (i)
    {
        temp = stk[--i];
        count++;//栈中弹出一个入度为0的顶点
        for (ArcNode* p = G.vertices[temp].fisrtarc; p ; p=p->nextarc)
        {
            if (!(--G.vertices[p->adjvex].indgree))stk[i++] = p->adjvex;//若有一个后继入度减为0则入栈
        }//删除这个顶点后，它的每一个后继的入度减一
    }
    if (count < G.vexnum)return false;//若拓扑序列并没有包含图中所有顶点则图中存在环
    else return true;
}

若一个有向图有n个顶点和e条弧，则该算法的时间复杂度为O(n+e)。入度为0的顶点入栈的时间复杂度为O(n)。若有向图无环，则每一个顶点都会入栈一次出栈一次，并且在这一个过程中还要进行该店后继入度减一的操作，它的次数和删除的边数是相等的，所以时间复杂度为O(e)。所以总共的时间复杂度为O(n+e)。

关键路径

与AOV网相对应的是AOE网（Activity On Edge）,即边表示活动，点表示事件，以该点为头的边表示已完成的活动，以该点为尾的边表示可以开始的活动。例如

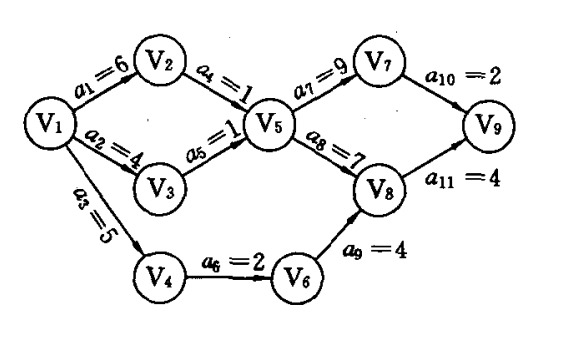
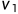
表示流程的开始，

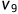
表示整个流程的结束，

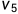
表示

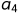
和

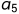
已经完成，

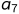
和

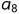
可以开始。每条边所带的权表示活动所需要的时间。所以整个流程（不出现环）只有一个入度为0的顶点（流程的开始，也叫源点）和一个出度为0的顶点（流程的结束，也叫汇点）。有些活动可以并行进行，所以完成整个流程的最短时间为整个有向图的最长路径（权值之和），这是因为最长路径的总时间下，其他活动都能并行完成。这个最长的路径叫做

关键路径。

关键路径下的活动是不会推迟开始或者延迟结束的，它们的所需时间之和正好够整个流程结束，所以它们的最早发生时间和最迟发生时间是相同的，我们记一个活动

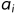
最早发生时间为

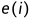
，最迟发生时间为

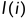
，所以关键路径下的活动

=

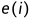
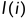
。而非关键路径下的活动

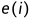
和

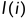
可以不同，它们推迟开始和延迟结束都不会对整个流程产生影响。所以只需要找到所有

=

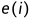
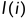
的活动，就找到了关键路径，也就找到了完成整个流程的最短时间。

为了求得

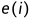
和

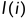
，我们可以先求得

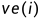
事件最早发生时间和

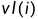
事件最迟发生时间,因为它们有以下公式（根据图来看），

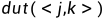
为

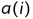
的时间

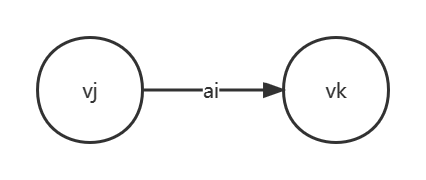
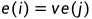
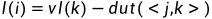
求

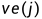
是一个递推的过程，从

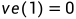
开始，

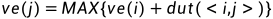
,其中

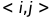
是所有以j为头的弧的集合。这个比较好理解，最晚完成的活动完成后，所有以该点为头的活动完成，该事件立马发生，即最早发生时间。

求

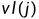
是一个逆着递推的过程，从

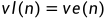
开始，

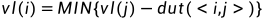
,其中

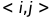
是所有以i为尾的弧的集合。事件最晚发生时间为所有以该事件为尾的活动

开始的时间，所以事件最晚发生时间为所有后继减去以该后继为头的活动的时间当中的最小值，因为该值保证了所有以该事件的后继为头的活动的完成。

所以求关键路径的算法描述为：从

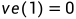
开始递推的计算

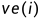
,再从

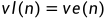
倒着递推的计算

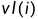
,然后根据上面的公式计算出

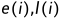
,然后根据

=

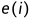
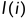
找出关键活动。计算各顶点的

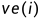
值是根据拓扑排序的过程来计算的，所以我们用栈存储这个拓扑序列，然后在逆向计算

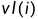
时的顺序就是栈的出栈顺序。

代码如下

bool TopologicalOrder(AlGraph G, int* T,int *ev)//先用拓扑排序的方法求出ev数组，所以拓扑排序的过程不再赘述
{
    int* stk = (int*)malloc(sizeof(int) * G.vexnum);
    int i = 0,j = 0;
    for (int v = 0; v < G.vexnum; v++)
    {
        if (!G.vertices[v].indgree)stk[i++] = v;
    }
    int count = 0;
    int temp;
    while (i)
    {
        temp = stk[--i];
        T[j++] = temp;//记录拓扑序列所用的栈
        count++;
        for (ArcNode* p = G.vertices[temp].fisrtarc; p; p = p->nextarc)
        {
            if (ev[p->adjvex] < ev[temp] + p->weight)ev[p->adjvex] = ev[temp] + p->weight;//
求ev数组所用的公式
            if (!(--G.vertices[p->adjvex].indgree))stk[i++] = p->adjvex;
        }
    }
    if (count < G.vexnum)return false;
    else return true;
}

bool CriticalPath(AlGraph G)
{
    int* ev = (int*)malloc(sizeof(int) * G.vexnum);
    int* lv = (int*)malloc(sizeof(int) * G.vexnum);
    int* T = (int*)malloc(sizeof(int) * G.vexnum);
    for (int v = 0; v < G.vexnum; v++)//初始化ev数组
    {
        ev[v] = 0;
    }
    if (!TopologicalOrder(G, T, ev))return false;//若图中存在环则终止
    lv[G.vexnum - 1] = ev[G.vexnum - 1];//流程结束的顶点lv等于ev
    int top = G.vexnum;
    while (top)
    {
        int temp = T[--top];//T出栈顺序则是lv的计算顺序
        for (ArcNode* p = G.vertices[temp].fisrtarc ; p; p = p->nextarc)
        {
            if (p == G.vertices[temp].fisrtarc)lv[temp] = lv[p->adjvex] - p->weight;//初始化当前顶点的lv
            if (lv[p->adjvex] - p->weight < lv[temp])lv[temp] = lv[p->adjvex] - p->weight;//根据公式计算lv
        }
    }
    for (int v = 0; v < G.vexnum; v++)
    {
        for (ArcNode* p = G.vertices[v].fisrtarc; p; p=p->nextarc)
        {
            int e = ev[v];
            int l = lv[p->adjvex]-p->weight;
            if (e == l)printf("%d->%d\n", G.vertices[v].data, G.vertices[p->adjvex].data);//求出关键活动
        }
    }
}