之前给大家介绍了搜索二叉树的非递归算法,今天给大家介绍一些搜索二叉树的递归算法的操作。
这里主要介绍的是插入,查找和删除。
其实插入和之前的二叉树的操作是一样的,不过依然是需要判断你要查入的元素应当插入的位置。
int BSTreeInsertR(BSTreeNode** tree, DataType x)
{
if (*tree == NULL)
{
*tree = BuyBSTreeNode(x);
return 0;
}
if ((*tree)->_data > x)
{
return BSTreeInsertR(&(*tree)->_left, x);
}
else if ((*tree)->_data < x)
{
return BSTreeInsertR(&(*tree)->_right, x);
}
else return -1;
}
依然是和非递归一样的判断条件,但是这里和细心的人会发现和非递归的区别,大家都知道二叉树和数组不同不是单纯的将数据放到该放的位置就行了,这里还需要做的是,你要将他的父亲结点和他链接起来,不然等会怎么去找刚插入的结点的呢?非递归的状态下我们是设置了一个parent,大家都知道函数是在栈上开辟空间并且运行的,所以你在当前函数创建一个变量,在下一个函数,或者返回到上一个函数的时候,这个临时变量会随着你栈的销毁而销毁。但是这里并没有parent这个变量,没有说将两个节点链接起来的操作,那他为什么会链接起来了呢?这里就是很巧妙的用了C语言指针的知识。
大家发现,这个函数所传的参数都是二级指针,就是因为二级指针才巧妙的将两个节点连接到了一起。
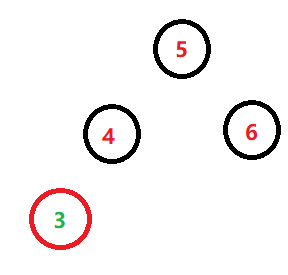
假如我们开始有三个节点456,现在我们需要将一个新的节点3插入进去,先说一下指针,4中有两个指针,其实可以简单的理解成,4中有两个存储数据的地方,3是4的左孩子,也就是说,4中两个存储数据的地方,有一个也就是左指针,它里边存放了3的地址,也就是这个地址他找到了3的存在,这里看我们的程序。3比5小那就往左走,3比4小继续往左走
return
BSTreeInsertR(&(*
tree
)->_left,
x
);
大家看这里当发现3比4小的时候,我们将4的左指针取地址传入了下一层函数中。然后让
*
tree
= BuyBSTreeNode(
x
);
4的左指针中的值等于新开辟的空间,这里就很好的让4的做指针指向了我们新插入的结点。
const BSTreeNode* BSTreeFindR(BSTreeNode* tree, DataType x)
{
if (tree == NULL)
{
return NULL;
}
if (tree->_data > x)
{
return BSTreeFindR(tree->_left, x);
}
else if (tree->_data < x)
{
return BSTreeFindR(tree->_right, x);
}
else
{
return tree;
}
}
这是我们递归版的查找算法,查找的时候不断的比较大小,这里和我们之前写的一个查找有所不同,之前有查找的时候需要通过一个数据来接受上一层函数的返回值,但是这里并不需要,为什么呢?因为这里并不会走你之前所走过的路。
并且找到之后会直接进行返回,比如我们现在要找刚刚插入的3,先传入5的结点,然后发现3比5小,直接进入第一层if语句,然后进入下一层函数,当找到3的时候,直接返回3的结点,然后退回到上一层的函数,这时候仍然是直接返回返回值,这样一层一层的再返回出去。
在非递归的时候最复杂的是我们的删除函数,但是当我们在非递归状态下,将删除的操作思考清楚之后,递归就变的相对简单了。
int BSTreeRemoveR(BSTreeNode** pptree, DataType x)
{
BSTreeNode*cur = *pptree;
BSTreeNode*del = cur;
BSTreeNode*sub = NULL;
if (NULL == *pptree)//空
{
return -1;
}
assert(pptree);
if (cur->_data>x)
{
return BSTreeRemoveR(&(cur->_left), x);
}
else if (cur->_data<x)
{
return BSTreeRemoveR(&(cur->_right), x);
}
else//找到后进行删除
{
del = cur;//记录要删除的点
if (cur->_left == NULL)//左为空
{
*pptree = cur->_right;
}
else if (cur->_right == NULL)//右为空
{
*pptree = cur->_left;
}
else//左右都不为空
{
sub = cur->_right;
while (sub->_left)
{
sub = sub->_left;
}
del = sub;
cur->_data = sub->_data;
return BSTreeRemoveR(&(cur->_right), sub->_data);
}
free(del);
del = NULL;
return 0;
}
}
这里先通过一层层递归找到你所要删除的结点,这里和插入是同一个道理,通过传入二级指针修改。这里我带大家走一次就会很清楚。
假如我现在要删除的结点是3,进来之后就要进入下一层循环,也就是这次传入的二级指针是5的左孩子的指针,现在指向的是4,4依然比3大,继续将4的左孩子指针传入下一层循环,再次进来之后,发现现在指向的数据不比要删除的数据大, 也不比要删除的数据小,说明这就是你当前要删除的数据。
这时候就进入了和非递归一样的状态,这时候还是去判断,这里也是二级指针立下了大功劳。
同样是,删除的话怎么让你要删除的结点的父亲指向你的孩子呢?
*
pptree
= cur->_right;
大家看,现在回到我刚刚说的例子。假如你现在要删除的是3,那你当前这一层递归传进来的是4的左孩子的二级指针,这里我们直接修改传进来的这个指针指向你要删除的结点的孩子就可以。
但是左右都不为空的情况,稍有不同,当左右都有孩子还是要去找
sub = cur->_right;
while (sub->_left)
{
sub = sub->_left;
}
要删除的结点的右孩子的最左结点,找到时候,让这个数据覆盖掉你删除的,之后你需要将你当前的这个节点删除,就需要再次进入一层要删除函数,这时候删除的结点,就是你的当前想要删除的结点,数据也就要改成你现在要删除的数据了,切记不能还是以前的数据,就会出现问题。
return
BSTreeRemoveR(&(cur->_right), sub->_data);
但是记住,你这些操作是在你最内一层的递归所完成的,这些操作都完成之后还是要不断的一层一层递归返回上去。这里返回的都是上一层递归的返回值,所以这里并不需要进行什么操作。
递归的搜索二叉树大致就是这样,我认为这里边最难以理解的就是二级指针的问题,所以要对指针有深刻的理解。这里我认为我介绍的也并不是很详细,如果大家有更好,更容易理解的方法, 可以留言给我。