之前我们学习了第二型曲线积分,主要学习内容是第二型曲线积分的计算,其积分微元为带有方向的弧线(曲线);而接下来的第二型曲面积分,也是主要学习它的计算方法,其积分微元是带有方向的曲面。两者有很多相通之处。
学习主要内容:
- 空间曲线的切向量


- 空间曲面的法向量

一、第一型曲面积分
首先我们先来回顾一下在第九章学过的第一型曲面积分——数量函数在曲面上的积分。
- 第一型曲面积分的计算
对于可积型曲面S: z = z(x, y),
, 曲面上任意一点处的法向量为
=
,
若投影到xOy平面,则求出对z轴的方向余弦
,
, 将z作为x、y的函数代入、并替换dS,得:

由于第一型曲面积分具有奇偶性、对称性两个重要性质,在解题计算中颇有运用。
例


画出图形后,观察到积分区域(一片球的表面),这个曲面关于x轴对称,因此若被积表达式中存在关于x的奇函数的项,则该项积分结果为零;对y同理。

对等性
,就是对积分曲线而言,我们任意轮换x、y、z(比如将x换成y,将y换成z、将z换成x),积分曲线不变(我们说积分曲线具有
轮换对称性
),那么该积分满足对等性(即x、y、z地位相同,被积表达式中也可以任意轮换x、y、z),有
.
例
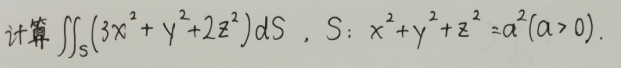
解:此处我们发现,给出的S曲面方程中任意轮换x、y、z后,方程不变,故具有对等性。

二、有向曲面与第二型曲面积分的概念
- 有向曲面
回顾一条直线段,它的方向由其方向向量指定(此时我们称其为向量),曲面不存在方向向量,但是存在法向量,因此借助法向量来指定曲面的方向:

- 几个微分关系
与曲线积分中的类似,有
- 第二型曲面积分的概念

- 第二型曲面积分与第一型曲面积分关系
由上可知:
- 第二型曲面积分的性质
-
有向性

-
线性性
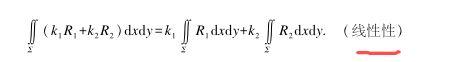
-
积分曲面可加性
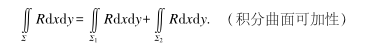
-

三、第二型曲面积分的计算
计算第二型曲面积分的第一种方法,是根据第二型曲面积分和第一型曲面积分的关系,以及第一型曲面积分的计算公式推导而来的。


- 关于方向与符号问题
以投影到xOy平面为例,可以想象,当单值曲面取上侧,法向量与z轴正向的夹角才是小于
的,转化后的二重积分取正号,反之取负号。
知识点5:分面计算法
由上看出,转化后的二重积分与z(x, y)的偏导数存在关系,但是有一项只需要乘以1即可,不用乘以偏导数,那就是dxdy这一项。那我们不妨做一些处理,只留下这一项,让转化后的二重积分形式更简洁。

启示我们的是,在计算一个普通的第二型曲面积分时,可以分别计算它投影到三个坐标面上的积分,即
操作步骤:
-
画出相应的图形,即对应的积分曲面大概长这么样子,方向如何;
-
分面投影,得到单值函数,代入原二型积分的被积表达式,并且
确定符号
,即得到二重积分;
-
根据上一步得出的坐标面上的投影,求出二重积分的积分区域
例
求
, 方向为上侧.
第一步
,

这个积分曲面是一个球面的一部分;
第二步
,分面投影,此处仅需要投影到zOx平面计算,显然,投影是一个四分之一圆面的扇形,代入y的值,符号为正,即可计算二重积分;

第三步
,将投影的扇形作为二重积分的积分区域,计算二重积分

例

观察到x+y+z=1,具有对等性,利用此性质解题

例

知识点5:统一坐标面计算
分面计算,一般情况下需要我们分三个坐标面投影再计算,也就是需要“投影、积分”操作三次,计算麻烦还不好说,很有可能我们连某个坐标面上的投影大致长啥样都不清楚,那么这样就有障碍了。
有没有什么更好的方法,可以绕开那些复杂的坐标面投影,只算我们熟悉的某一个坐标面投影上的二重积分呢?
让我们回到最开始推导第二型曲面积分的计算公式时:

也就是说,我们最开始就已经得到了统一到xOy坐标面内的计算公式 ,类似的三个坐标面上的统一投影计算公式如下,选取原则为哪个坐标面上的投影熟悉就用哪个。

例
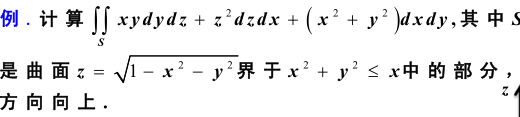
解:首先也是作出大致图形,
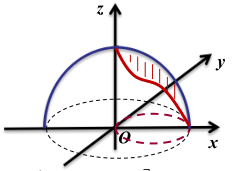
其次,我们很难想象这部分曲面投影到zOx平面或者yOz平面是什么样子,但是根据柱面的特点,我们知道,这部分曲面投影到xOy平面一定是一个圆,那么就可以都投影到xOy平面内计算二重积分了。
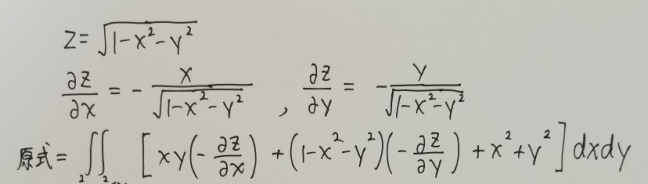
注意,一旦将第二型曲面积分转化为二重积分之后,就不可以再随意化简积分不等式了,
但是,却可以使用对称性(奇偶性)简化运算
;

最后计算二重积分即可,用到了极坐标变换,注意要变换后还要乘以雅可比行列式(这里是r)
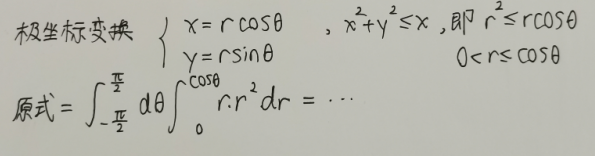
三、高斯公式
知识点6:高斯公式的内容与理解

定理的使用前提:
- 由闭曲面围成空间闭区域;
- 函数在该闭区域上具有连续的一阶偏导数
- 高斯公式默认计算的是曲面外法方向的积分
对于立体表面而言,法线是有方向的,对应有向曲面的方向:
一般来说,由立体的外部指向内部,就是曲面的
内法方向
,反过来,由立体的内部指向外部,就是曲面的
外法方向
。
高斯公式的使用与格林公式有
相似之处
,比如
- 最开始看看是否可以对被积表达式进行化简;
- 求出三个偏导数之和,看看方不方便使用三重积分计算(格林公式则为二重积分);
- 检验满不满足公式的前提
- 不满足则需要补面(格林公式则需要补线),补的面一般与坐标面平行(正如补的线一般与坐标轴垂直)
知识点7:灵活使用高斯公式
例

先小结一波计算第二型曲面积分的步骤:
- 作图,大致画出积分曲面的形状;
-
对被积表达式进行尽可能的化简;
- 计算三个偏导数之和,看看适不适合使用高斯公式;
- 对于分面计算、统一计算,按照之前的路子计算二重积分即可;
-
对于高斯公式,首先检验其使用条件;
-
对于不满足条件的,补面;
-
转化为三重积分,注意调整符号;
-
通常用分面计算方法计算补上的面的二型积分,作差即可;
例
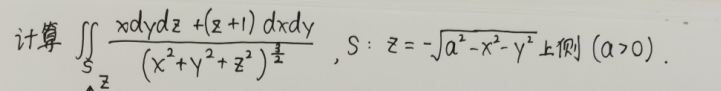
第一步
,作图,这是半个球面
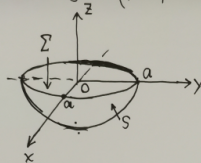
第二步
,化简被积表达式
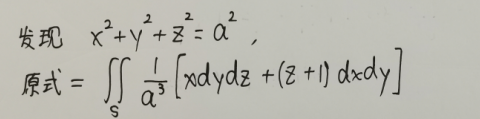
第三步
,预先计算三个偏导数之和,发现结果很简洁,适用高斯公式
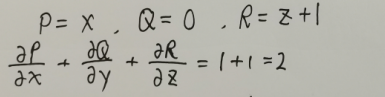
第四步
,检验高斯公式的使用条件,发现并不是空间闭区域,故需要补面(与坐标面平行),确保围成空间闭区域

第五步
,转化为三重积分,注意符号
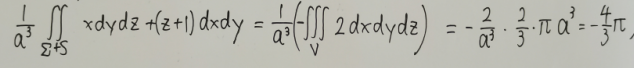
第六步
,求补上的面上的二型曲面积分(注意符号),并减去


复连通域上的高斯公式

例
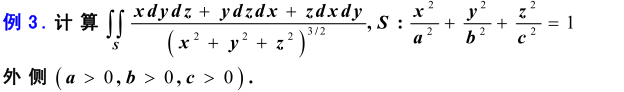
解:很遗憾,最开始不可以化简被积表达式,所以只能耐着性子求偏导数之和,

结果很简洁,为0,那么高斯公式石锤。
检验使用条件,发现(0, 0, 0)处没有一阶连续偏导数,所以需要“挖点”,即补面(闭合曲面),与格林公式中的补线类似,也要考虑之后的运算简便性。


接下来就是求补上的面的二型积分,此处就可以代入去掉分母,但是也要注意符号。
