一、数学原理分析

线性回归

当两个变量存在准确、严格的直线关系时，可以用Y=a+bX，表示两者的函数关系。

其中X 为自变量（independent variable）；Y是因变量（ dependent variable ）。

但在实际生活当中，由于其它因素的干扰，许多双变量之间的关系并不是严格的函数关系，不能用函数方程来准确反映，为了区别于两变量间的函数方程，我们称这种关系为回归关系，用直线方程来表示这种关系称为回归直线或线性回归。

最小二乘法

计算原理：最小二乘法，即保证各实测点到回归直线的纵向距离的平方和最小，并使计算出的回归方程最能代表实测数据所反映出的直线趋势。

相关公式：









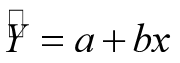
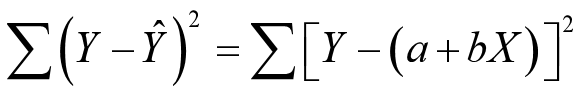
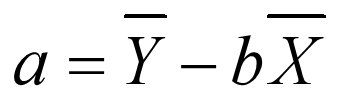
Y的总变异分解：

R的平方取值在0到1之间，反映了回归贡献的相对程度。

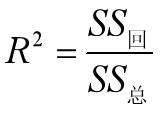
二、EXCEL简单处理

处理的

文件地址

，可自行下载。

20组数据

使用excel绘制的图片：

200组数据

使用excel绘制的图片：

2000组数据

使用excel绘制的图片：

20000组数据

使用excel绘制的图片：

三、python语言设计最小二乘法计算（使用anaconda的jupyterlab）

使用工具介绍

使用了Anaconda里的一个工具jupyterlab，可在

Anaconda官网

自行下载。

打开anaconda里的jupyterlab，将会以网页方式打开：



点击python创建一个文件：

不调用包的python计算

#不掉包实现一元线性回归
import pandas as pd
def read_file(raw):#根据行数来读取文件
    df = pd.read_excel('..\\source\\weights_heights(身高-体重数据集).xls',sheet_name ='weights_heights')
    height=df.iloc[0:raw,1:2].values
    weight=df.iloc[0:raw,2:3].values
    return height,weight

def array_to_list(array):#将数组转化为列表
    array=array.tolist()
    for i in range(0,len(array)):
        array[i]=array[i][0]
    return array

def unary_linear_regression(x,y):#一元线性回归，x,y都是列表类型
    xi_multiply_yi=0
    xi_square=0;
    x_average=0;
    y_average=0;
    f=x
    for i in range(0,len(x)):
        xi_multiply_yi+=x[i]*y[i]
        x_average+=x[i]
        y_average+=y[i]
        xi_square+=x[i]*x[i]
    x_average=x_average/len(x)
    y_average=y_average/len(x)
    b=(xi_multiply_yi-len(x)*x_average*y_average)/(xi_square-len(x)*x_average*x_average)
    a=y_average-b*x_average
    for i in range(0,len(x)):
        f[i]=b*x[i]+a
    R_square=get_coefficient_of_determination(f,y,y_average)
    print('R_square='+str(R_square)+'\n'+'a='+str(a)+'  b='+str(b))
    
def get_coefficient_of_determination(f,y,y_average):#传输计算出的值f和x,y的真实值还有平均值y_average，获取决定系数，也就是R²
    res=0
    tot=0
    for i in range(0,len(y)):
        res+=(y[i]-f[i])*(y[i]-f[i])
        tot+=(y[i]-y_average)*(y[i]-y_average)
    R_square=1-res/tot 
    return R_square

raw=[20,200,2000,20000]
for i in raw:
    print('数据组数为'+str(i)+":")
    height,weight=read_file(i)
    height=array_to_list(height)
    weight=array_to_list(weight)
    unary_linear_regression(height,weight)

点击运行：



得到结果（可与excel的进行对比）：

调用包的python计算

与上面过程一样，只是代码发生了变化，调用了pandas的sklearn方法,会使代码简单一点，不用自己敲写算法：

#调包实现一元线性回归
from sklearn import linear_model
from sklearn.metrics import r2_score
import numpy as np
import pandas as pd
def read_file(raw):#根据行数来读取文件
    df = pd.read_excel('D:\weights_heights(身高-体重数据集).xls',sheet_name ='weights_heights')
    height=df.iloc[0:raw,1:2].values
    weight=df.iloc[0:raw,2:3].values
    return height,weight

raw=[20,200,2000,20000]#要读取的行数
for i in raw:
    print('数据组数为'+str(i)+":")
    height,weight=read_file(i)
    weight_predict=weight
    lm = linear_model.LinearRegression()
    lm.fit(height,weight)
    b=lm.coef_
    a=lm.intercept_
    weight_predict=lm.predict(height)#计算有方程推测出来的值
    R_square=r2_score(weight,weight_predict)#计算方差
    print('b='+str(b[0][0])+' a='+str(a[0]))
    print('R_square='+str(R_square))

得到结果：

四、参考材料

weights_heights(身高-体重数据集).xls



简单线性回归 (统计学角度).ppt