参考：

https://wenku.baidu.com/view/338d09ffc4da50e2524de518964bcf84b8d52ded.html

1.基本概念

（1）解决的问题

常见的现象：

上、下班搭乘公共汽车;顾客到商店购买物品;病员到医院看病;旅客到售票处购买车票;学生去食堂就餐等就常常出现排队和等待现象，

排队的不一定是人也可以是物

。


解决：

面对拥挤现象，人们总是希望尽.量设法减少排队，通常的做法是增加服务设施。但是增加的数量越多，人力、物力的支出就越大，甚至会出现空闲浪费，如果服务设施太少，顾客排队等待的时间就会很长，这样对顾客会带来不良影响。于是，

顾客排队时间的长短与服务设施规模的大小

，就构成了

随机服务系统

中的一对矛盾。

如何做到

既保证一定的服务质量指标，又使服务设施费用经济合理

，恰当地

解决顾客排队时间与服务设施费用大小

这对矛盾，这就是

随机服务系统理论一排队论

所要研究解决的问题。

（2）排队系统（又被称为：随机服务系统）的特征

实际的排队系统虽然千差万别，但是它们有以下的共同特征:

(1)有请求服务的人或物一

顾客

;

(2)有为顾客服务的人或物，即

服务员或服务台

;

(3)

随机性是排队系统的一个普遍特点。顾客到达系统的时刻是随机的，为每一位顾客提供服务的时间是随机的

,因而整个排队系统的状态也是随机的。排队系统的这种随机性

造成某个阶段顾客排队较长，而另外一些时候服务员(台)又空闲无事

。


任何一个排队问题的排队过程都可以用下图表示:




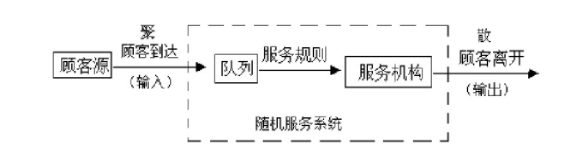
（1）每个顾客由顾客源按一定方式到达服务系统

（2）加入队列排队等待接受服务

（3）服务台按一定规则从队列中选择顾客进行服务

（4）获得服务的顾客立即离开

（3）排队系统的基本组成部分

（3.1）组成部分

通常，排队系统都有

输入过程、服务规则和服务台

等3个组成部分。

（3.2）输入过程

这是指要求服务的顾客是

按怎样的规律到达排队系统的过程

，有时也把它称为

顾客流

。一般可以从3个方面来描述一个输入过程：


(1) 顾客总体数，又称顾客源、输入源

。

这是指顾客的来源。顾客源

可以是有限的，也可以是无限的

。例如，到售票处购票的顾客总数可以认为是无限的，而某个工厂因故障待修的机床则是有限的。


(2)顾客到达方式。


这是描述顾客是怎样来到系统的，他们是

单个到达，还是成批到达

。病人到医院看病是顾客单个到达的例子。在库存问题中如将生产器材进货或产品入库看作是顾客，那么这种顾客则是成批到达的。


(3)顾客流的概率分布或称相继顾客到达的时间间隔的分布


这是求解排队系，统有关运行指标问题时，首先需要确定的指标。这也可以理解为

在一定的时间间隔内到达K个顾客(K=1、2、…) 的概率是多大。顾客流的概率分布一般有定长分布、二项分布、泊松流(最简单流)、爱尔朗分布等若干种。

（3.3）服务规则

这是指

服务台从队列中选取顾客进行服务的顺序

。一般可以分为

损失制、等待制和混合制

等3大类。

(1)损失制。这是指如果顾客到达排队系统时，所有服务台都已被先来的顾客用，那么他们就自动离开系统永不再来

。典型例子是，如电话拔号后出现忙音，顾客不愿等待而自动挂断电话，如要再打，就需重新拔号，这种服务规则即为损失制。

(2) 等待制。这是指当顾客来到系统时，所有服务台都不空，顾客加入排队行列等待服务。

等待制中，服务台在选择顾客进行服务时，常有

如下四种规则:



①先到先服务。

按顾客到达的先后顺序对顾客进行服务，这是最普遍的情形。


②后到先服务。

仓库中迭放的钢材，后迭放上去的都先被领走，就属于这种情况。


③随机服务。

即当服务台空闲时，不按照排队序列而随意指定某个顾客去接受服务。


④优先权服务。

如老人、儿童先进车站;危重病员先就诊均属于此种服务规则。

(3)混合制.

这是

等待制与损失制相结合

的一种服务规则，

一般是指允许排队，但又不允许队列无限长下去。

具体说来，大致有三种:


①队长有限。

当排队等待服务的顾客人数超过规定数量时，后来的顾客就自动离去，另求服务，即

系统的等待空间是有限的

。例如最多只能容纳K个顾客在系统中，当新顾客到达时，若系统中的顾客数(又称为队长)小于K,则可进入系统排队或接受服务;否则，便离开系统，并不再回来。


②等待时间有限。

即

顾客在系统中的等待时间不超过某一给定的长度T

，当等待时间超过T时，顾客将自动离去,并不再回来。如顾客到饭馆就餐，等了一定时间后不愿再等而自动离去另找饭店用餐。


③逗留时间(等待时间与服务时间之和)有限。



损失制和等待制可看成是混合制的特殊情形

，如记s为系统中服务台的个数，则当K=s（系统中的顾客数=服务台的个数）时，混合制即成为损失制；当K=∞时，混合制即成为等待制。

（3.4）服务台

（1）服务台的数量及其构成方式



数量上分为：

单服务台 和多服务台


从构成形式上看分为：


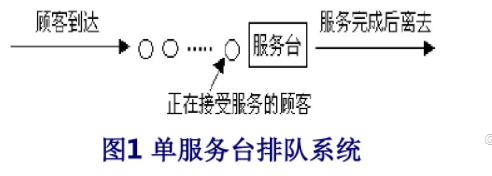
①单队-单服务台式;

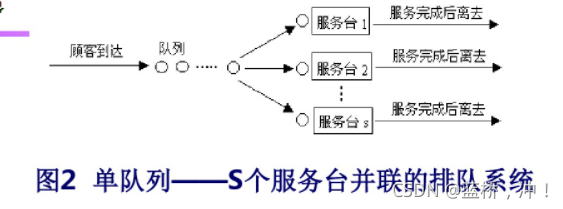
②单队-多服务台并联式;

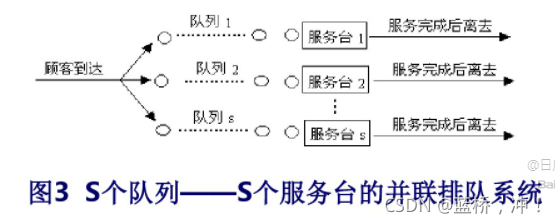
③多队-多服务台并联式;

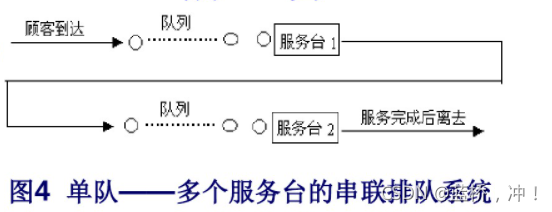
④单队-多服务台串联式;

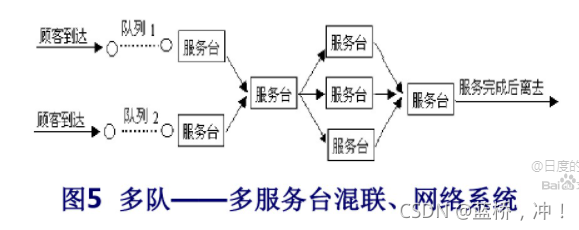
⑤单队-多服务台并串联混合式，以及多队-多服务台并串联混合式等等。


（2）服务方式


这是指在某一时刻接受服务的顾客数，它有

单个服务和成批服务两种

。如公共汽车一次就可装载一批乘客就属于成批服务。


（3）服务时间的分布


在多数情况下，对每一个顾客的服务时间是一随机变量，其概率分布有定长分布、负指数分布、K级爱尔良分布、一般分布(所有顾客的服务时间都是独立同分布的)等等。

（4）排队系统的描述符号

为了 区别各种排队系统，根据

输入过程、排队规则和服务机制

的变化对排队模型进行描述或分类，可给出

很多排队模型。为了方便对众多模型的描述，肯道尔(D. G. Kendall) 提出了一种目前在排队论中被广泛采用

的“

Kendal1记号

”，完整的表达方式通常用到6个符号并取如下固定格式:

A/B/C/D/E/F

（5）排队系统的主要数量指标

队长：

指系统中的平均顾客数(

排队等待的顾客数与正在接受服务的顾客数之和

)


排队长：

指系统中

正在排队等待服务的平均顾客数

。


等待时间：从顾客到达时刻起到他开始接受服务止这段时间称为等待时间

，通常希望等待时间越短越好。


逗留时间：


从顾客到达时刻起到他接受服务完成止这段时间称为逗留时间

，也是随机变量，同样为顾客非常关心。


忙期（服务台关心的）

：

指从顾客到达空闲着的服务机构起，到服务机构再次成为空闲止的这段时间，即服务机构连续忙的时间。

它关系到服务员的服务强度


闲期（服务台关心的）即服务机构连续保持空闲的时间。

在排队系统中，忙期和闲期总是交替出现的。

除了上述几个基 本数量指标外，还会用到其他一些重要的指标，如在损失制或系统容量有限的情况下，由于顾客被拒绝，而使服务系统受到损失的

顾客损失率及服务强度等，也都是十分重要的数量指标。

（6）一些数量指标的常用记号

λ：单位时间顾客平均到达数，即

顾客到达率


μ：单位时间平均服务的顾客数，即

服务率


N(t)：时刻t系统中的顾客数，即

队长


N

_q

(t)：时刻t系统中排队的顾客数，

即排队长


T(t)：时刻t到达系统的顾客在系统中的

逗留时间


T

_q

(t)：时刻t到达系统的顾客在系统中的

等待时间

这些随机变量的

瞬时分布一般是很困难的

。为了简便，并注意到相当一部分排队系统在运行了一定时间后，都会趋于一个

平衡状态(或称平稳状态)

。在平衡状态下，队长的分布、等待时间的分布和忙期的分布都

和系统所处的时刻无关，而且系统的初始状态的影响也会消失

。因此，我们主要讨论与系统所处时刻无关的性质，即

统计平衡性质。

L

_s

或L：

平均队长。即稳态系统任一时刻的所有顾客数的期望值;


L

_q

：

平均等待队长或队列长。即稳态系统任一时刻的等待服务的顾客数的期望值;


W或W

_s

：

平均逗留时间。即(在任意时刻)进入稳态系统的顾客逗留时间的期望值;


W

_q

：

平均等待时间。即(在任意时刻)进入稳态系统的顾客等待时间的期望值。



这四项主要性能指标(又称主要工作指标)的值越小，说明系统排队越少，等待时间越少，因而系统性能越好。

2.排队模型

（1）单服务台 泊松到达、负指数服务时间的排队模型（M/M/1）

（2）多服务台 泊松到达、负指数服务时间的排队模型（M/M/c）

（3）单服务台 泊松到达、任意服务时间的排队模型(M/G/1)

（4）单服务台 泊松到达、定长服务时间的排队模型(M/D/1)

（5）多服务台 泊松到达、任意服务时间的排队模型（M/G/c/0）->损失制

（6）顾客来源有限制的排队模型（M/M/1/∞/m）->顾客来源有限，即只有m个顾客

（1）单服务台泊松到达、负指数服务时间的排队模型（M/M/1）

例题：

case1：提高服务率





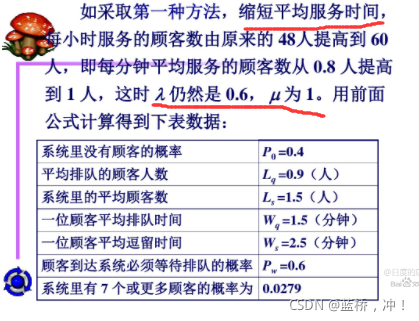
case2：增加一个服务台，但仍然是M/M/1的模型，只不过是2个

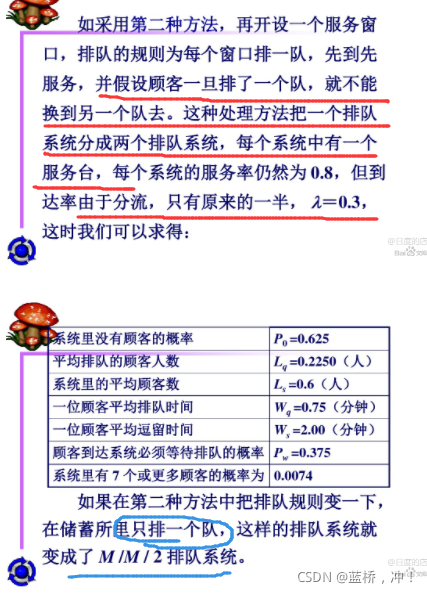
（2）多服务台泊松到达、负指数服务时间的排队模型（M/M/c）

这种排队模型我们记为

M/M/c/∞/∞

，这与前面的

区别就在于服务台的数量为c

。在M/M/c模型里，其到达过程为

泊松流

，每个服务台的服务时间分布为同样的

负指数分布

，排队的长度与顾客的来源都无限制，其排队规则为只排一个队，

先到先服务

，当其中一个服务台有空时，排在第一个的顾客就上去接受服务。

例题：M/M/2模型




与前面2个M/M/1的区别：服务台数量都是2；顾客到达率和服务率一样；但是2个M/M/1是排2队，M/M/2是排1队，M/M/2使得服务水平更高了。


排队系统的经济分析：

（3）单服务台泊松到达、任意服务时间的排队模型(M/G/1)

例题：

（4）单服务台泊松到达、定长服务时间的排队模型(M/D/1)

例题：

（5）多服务台泊松到达、任意服务时间的排队模型（M/G/c/0）->损失制

这种排队模型是一种

损失制的模型

，它要解决的主要问题是

在服务机构的空闲与顾客的流失之间找到平衡，找出最合适服务台数，使得该系统收益最大。


注:该排队模型

不存在

平均排队的顾客数L

_q

和顾客平均的排队等待时间W

_q





例题：

（6）顾客来源有限制的排队模型（M/M/1/∞/m）->顾客来源有限，即只有m个顾客

例题：

3.排队系统的优化目标与最优化问题

以完全消除排队现象为研究目标是不现实的

，那会造成服务人员和设施的严重浪费，但是设施的不足和低水平的服务，又将引起太多的等待，从而导致生产和社会性损失。

1. 从经济角度考虑，排队系统的费用应该包含以下两个方面：一个是
   
   服务费用
   
   ，它是服务水平的递增函数;另一个是
   
   顾客等待的机会损失(费用)
   
   ，它是服务水平的递减函数。两者的总和呈一条U形曲线。
2. 排队系统常见的优化问题在于：
   
   
   
   
   研究排队系统的根本目的在于：
   
   以最少的设备得到最大的效益，或者说，在一定的服务质量的指标下要求机构最为经济。排队系统的最优化问题分为两大类:静态最优设计问题和动态最优控制问题。