临时备考用,有许多未完善地方,有错误欢迎纠正
数值计算的误差:模型误差、观测误差(数据误差)、截断误差(方法误差)、舍入误差。在数值分析中主要讨论截断误差及舍入误差。
设 x* 是准确值x的一个近似值, 称 e(x*) = x*-x为近似值x
的
绝对误差
, 简称误差.。 e(x
)又简记e*。e
r
为近似值 x
的
相对误差
。e
r
=(x
-x)/x。
有效数字
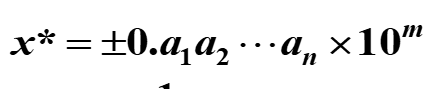
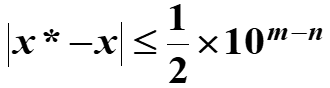
这里面的n即为有效数字。
避免误差危害的若干原则
1.避免除数的绝对值远小于被除数的绝对值。 2.注意避免两个相近数的相减。3.即避免两个相差很大的数作加法运算 。4.简化计算步骤, 减少运算次数。5.使用数值稳定的算法。
误差估计

插值法
设 y= f(x) 是区间[a , b] 上的一个实函数, xi ( i=0, 1, … ,n)是[a,b]上n+1个互异实数,已知 y=f(x) 在 xi 的值 yi=f(xi) (i=0,1,…,n), 求一个次数不超过n的多项式Pn(x)使其满足Pn(xi)=yi (i=0,1, …, n) ,此为
插值条件
。这就是
多项式插值问题
。
其中Pn(x) 称为 f(x) 的n次插值多项式, f(x) 称为
被插函数
, xi(i=0,1, …,n)称为
插值节点
, (xi, yi) (i=0,1, … ,n) 称为
插值点
, [a,b] 称为
插值区间
。
拉格朗日插值多项式
不超过n的多项式
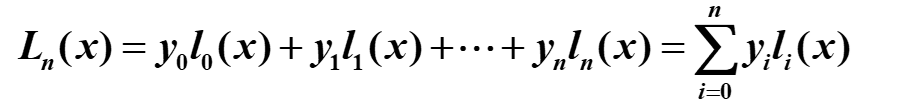
y
n
为对应点的值。l
i
中不含对应的第i项。

当 n =1时又叫线性插值,其几何意义为过两点的直线. 当 n =2时又叫抛物(线)插值。注意这里的点是从0开始数的,n=1实际上是两点的插值。
对于插值节点,只要求它们互异,与大小次序无关
插值余项
这里的ξ是介于区间中的一个不确定的值。
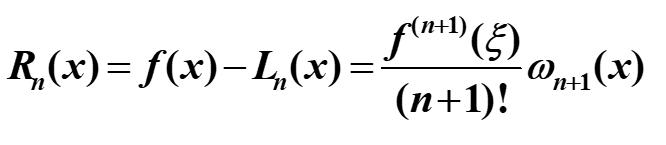
其中
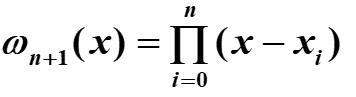
有一结论:
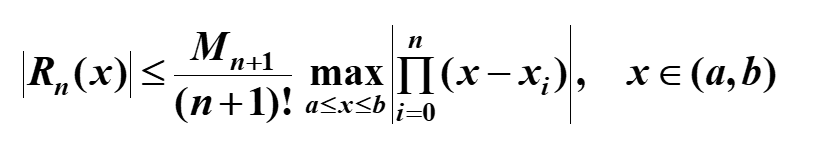
M
n+1
为max|f
(n+1)
(x)|
均差(差商)
此为一阶均差(差商)
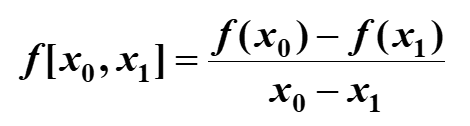
在这n+1个点处的n阶均差
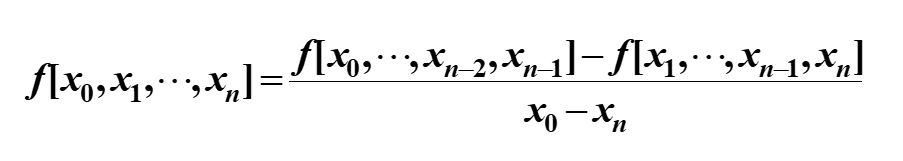
一般解题的时候列均差表

均差与节点的排列次序无关,无序将点进行排序
若f(x)在[a,b]上存在n阶导数, 且节点x0 , x1 ,…, xn∈[a,b] ,则至少存在一点ξ∈[a, b] 满足下式
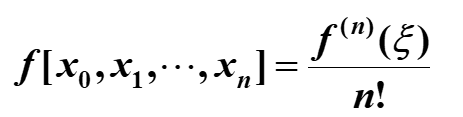
解题时f的阶数可能与n相等,这样求导后为常数就与ξ无关了。
牛顿插值多项式
只有牛顿插值具有承袭性,即添加数据不需要重头计算。
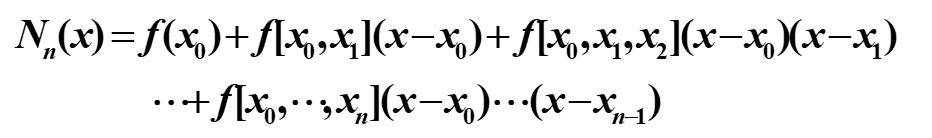
余项
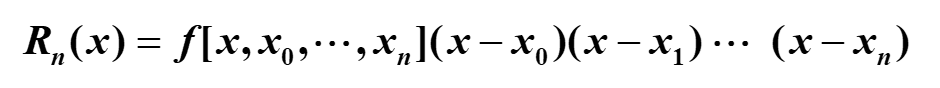
差值多项式是唯一的,所以这里的余项也可以用上面的表示
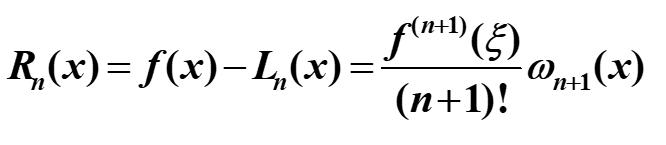
差分
设函数y=f(x)在等距节点xi=x0+ih (i=0,1, …,n)上的函数值为fi=f(xi)(h为步长)
一阶前向差分
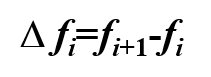
一阶后向差分
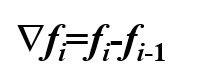
差分表

也可表示为

均差与差分的关系

等距节点插值公式
与牛顿的区别在于它在选节点的时候强调了等距,其他与牛顿相同他,可以直接带进去。这样原牛顿中的n项x-x
i
就包含了h
n
与上方换算称均差的分母部分h
m
抵消掉。
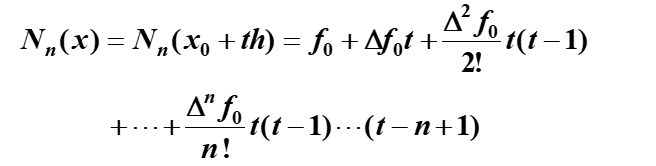
余项
t部分是-号,这里写错了。
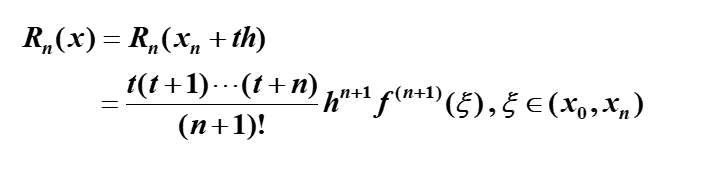
埃尔米特插值多项式
在给出含导数问题时一般使用。实际上就是在列均差的时候将给出导数的点写两遍。
例如 f(1)=2 f’(1)=4,那么列表时
| x | y | 一阶 |
|---|---|---|
| 1 | 1 | \ |
| 1 | 1 | 4 |
余项,与上面一样的算法(这是三阶的)
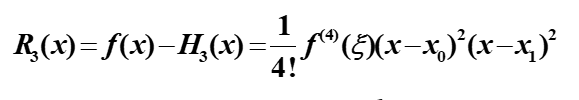
三次样条函数
S特点
1.S(xi )=yi (i=0,1,…,n);
2.在每个小区间[xi, xi+1] (i=0,1,…,n-1)上是次数不超过3的多项式;
3.在每个内节点xi (i=1,2,…,n-1)上具有二阶连续导数,则称 S(x) 为关于上述划分的一个三次多项式样条函数,简称三次样条。
函数逼近(曲线拟合)
用简单的函数P(x)近似代替函数f (x),f (x)称为逼近(被拟合)函数, P(x)称为逼近(拟合)函数。
C[a, b],表示函数在ab的闭区间内连续,当C上方有角标数字,数字即代表具有几阶连续偏导。
S=span{x1,…,xn},并称空间S为
n维空间
,其中x1,…,xn为线性无关的元素(这里的线性无关与向量中的定义一样)。
范数
性质:

常用的范数:无穷范数,一范数,二范数
对于函数就是图中的积分,对于向量x将积分改为求和即可。

内积
x=(x1,x2,…,xn)
T
,y=(y1,y2,…,yn)
T
内积(x, y)= x1
y1 +x2
y2 +…+xn*yn
线性空间中满足性质

最佳逼近
f为原函数,P*为逼近函数
使用最大范数表达时为最佳一次逼近
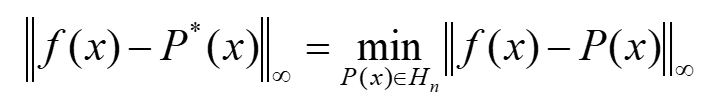
使用二范数表达时为最佳平方逼近
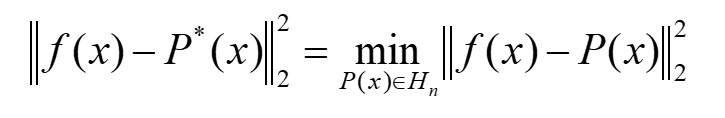
勒让德多项式
当区间[-1,1], 权函数ρ(x)≡1时, 由{1,x,…,xn,…}正交化得到的多项式就称为勒让德(Legendre)多项式
再高阶不会考(我们这里)

对零的平方误差最小
切比雪夫多项式
权函数为1/(1-x
2
)
0.5
,区间为[-1,1]时,由序列{1,x,…,xn,…}正交化得到的多项式就是切比雪夫多项式

对任意n次多项式有
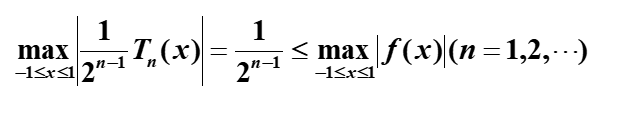
这个式子用于求n次多项式函数的n-1次最佳(一致)逼近多项式函数。
在所有首项系数为1的n次多项式中,对零的一致误差最小
最佳一次逼近
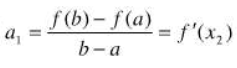
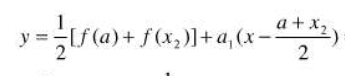
最佳平方逼近
题中会问是n次最佳平方逼近
原方程为f,设方程为S*=a
0
+a
1
φ
1
+…a
n
φ
n
n
,()中计算使用积分,上下限就是题中给出的区间,求解后带回即可。

最小二乘法
设拟合方程为(几次就写到几,这里以二次为例),如果题中有额外条件导致有些项为零,后面项补上。
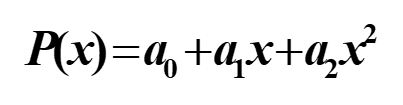
列法方程(更高次类推)

正交多项式
函数族φ在[a,b]上连续的正交函数族。则满足
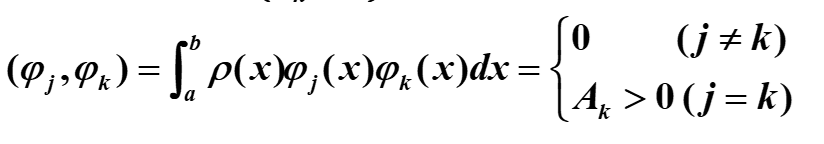
若A
k
恒等于1,称之为标准正交函数族。
数值积分与数值微分
要验证一个求积公式具有m次代数精度,只要令对于 f(x)=1, x,x
2
…求积公式精确成立等式就行,直到不相等。
数值积分
区间[a,b]上的f(x)
梯形公式
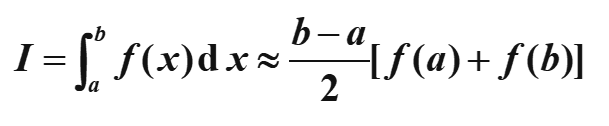
中矩形公式
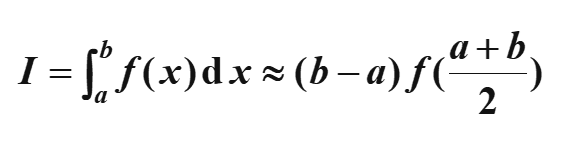
复合梯形求积公式余项
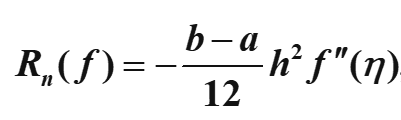
插值求积公式
用拉格朗日插值来近似代替原函数计算。

余项
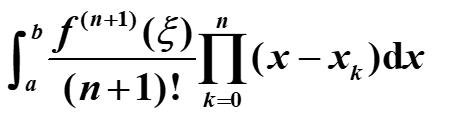
这样的插值替代,如果使用n+1个节点,至少具有n次精度。
牛顿—柯特斯公式
公式的系数C的和为1,且与积分区间无关
将区间[a,b]n
等分
,步长h=(b-a)/n,即插值节点选取x
k
=a+kh (k = 0,1,…,n)
n=1时为梯形公式
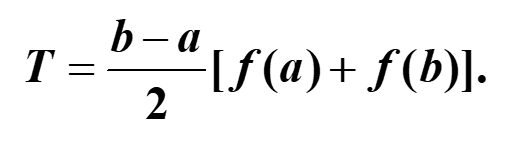
n=2时为辛普森(simpson)公式(又称为抛物形求积公式)
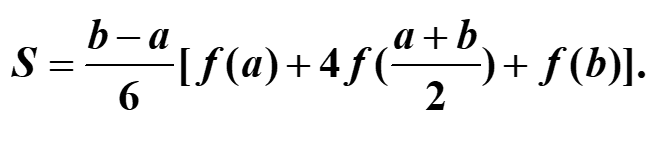
n=4为科特斯公式
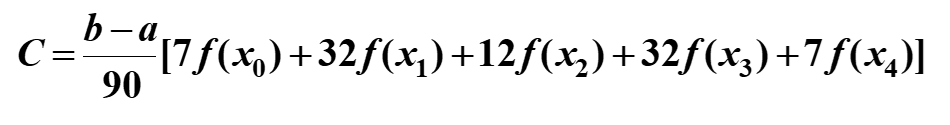
n >7的牛顿-柯特斯公式是不稳定的
n 阶牛顿-柯特斯公式的代数精度至少为
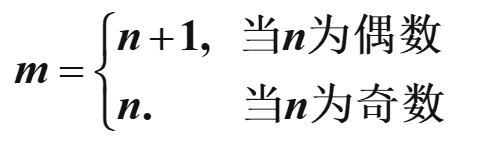
高斯求积公式
不固定节点的位置,在节点数目不变的情况下,最高代数精度的求积公式,具有2n+1次代数精度
高斯-勒让德求积公式
高斯求积公式的积分区间变为[-1,1]
两点
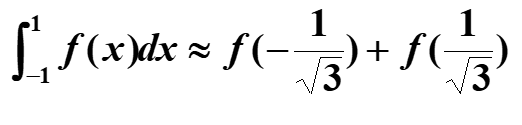
三点
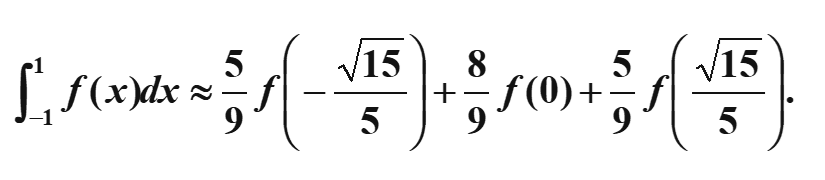
泰勒展开
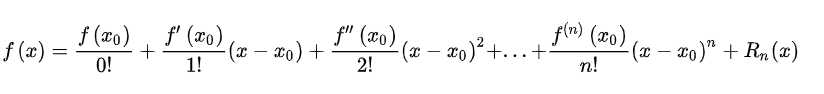
数值微分
两点公式
给出两点x
0
x
1
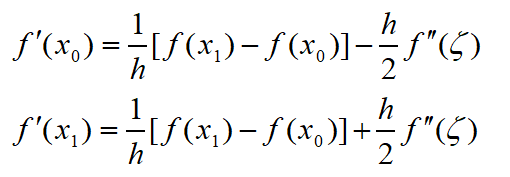
式中f那项是余项
三点公式
给出三点x
0
x
1
x
2

式中f那项是余项
解线性方程组的直接方法
高斯消去法
普通的方程组求解方法。化为三角矩阵求解。
矩阵三角分解
直接三角分解法(LU分解)


平方根法LDL
T
能进行分解的条件:设A为n阶对称矩阵,且A的各阶顺序主子式均不为零
L的计算公式
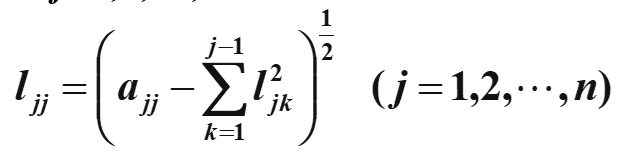
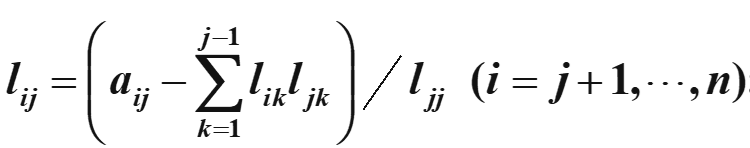



误差分析
b发生扰动
1.
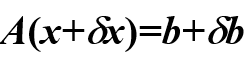
2.
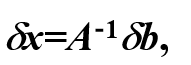
3.
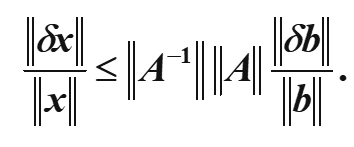
A发生扰动
1.
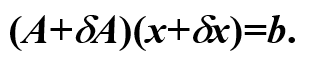
2.

解线性方程组的迭代方法
Ax=b的雅可比迭代与高斯赛德尔迭代均收敛的条件:1.A为严格对角占优(主对角线的值在其对应行中最大)。2.A为弱对角占优(可以相等),且不可约(所有元素非零)。
迭代法收敛条件,迭代矩阵谱半径小于1
谱半径为该矩阵的特征值λ的绝对值的最大值(如果是虚数的话就计算平方开根号)
雅可比(Jacobi)迭代法

J(雅可比矩阵计算)

高斯-赛德尔迭代法
计算公式(分量形式),等式左边分别为x
1
,x
2
…x
n
,b与其他部分在右侧,左侧保证系数为一。形式如下,注意上面的角标

B矩阵的计算方法:B=(D-L)
-1
U
牛顿(Newton)迭代公式(切线法)
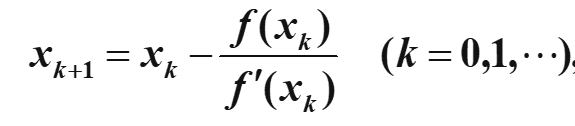
幂法
步骤

一般取v
0
=[1,1]
T
设A的特征值|λ
1
|≥|λ
2
|≥|λ
3
|≥…≥|λ
n
|,则A按模最大特征值的收敛速度与|λ
2
|/|λ
1
|有关
x
为单根时,牛顿迭代法在根x
的邻近是二阶(平方)收敛的
欧拉法
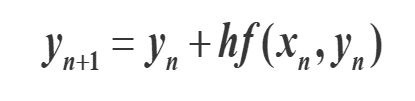
其中x
n
=n*h
改进欧拉法

也可以写作
