线性分类器其实我已经接触不少了，不同于KNN，它涉及到了更多的知识，比如cost function, objective function等，svm涉及到的知识确实比较多且难理解，但当我们得到相应公式后其实实现起来并不算繁琐，相反很容易理解

线性SVM

目标函数

目标函数我们在以前的线性回归，逻辑回归中都见到过

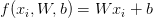
代价函数

SVM的代价函数想要SVM在正确分类上的得分始终比不正确分类上的得分高出一个边界值delta, 所以它的代价函数如下：

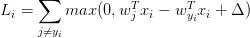
即在确定正确分类的分数（scores[y[i]]）后，其他分类上的分数都要减去它并且加上一个边界值 ( scores[y[!i] – screos[y[i]] + delta )，当得到的值小于0时则代表正确分类比不正确分类高出了一个边界值，否则则要计算损失值。

比如，假设有3个分类，并且得到了分值[13, -7, 11], 第一个分类为正确分类，delta为10，那么根据代价函数，我们可以得到以下算式

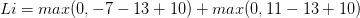
以上代价函数计算公式称为折叶损失（hinge loss），当然除此之外还有平方折叶损失SVM（即L2-SVM），就是加个平方，我们可以通过交叉验证或者验证集来确定到底选用哪个

正则项

在ML中，过拟合问题一直是影响模型准确率的重大因素，所以我们还要加上L2范式正则项（在这里，正则项还确保了SVM有最大边界（max margin）等好处），所以最终我们得到以下整个代价函数公式

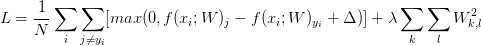
梯度计算

在训练过程中