本文转载自:http://www.360doc.com/content/17/0810/21/37752273_678258912.shtml
对协方差矩阵的特征向量最直观的解释之一是:它总是指向数据方差最大的方向。
更准确地说,第一特征向量是数据方差最大的方向,第二特征向量是与第一特征向量垂直方向上数据方差最大的方向,第三特征向量是与第一和第二特征向量垂直的方向上数据方差最大的方向,以此类推。
下图是二维空间的一个例子:
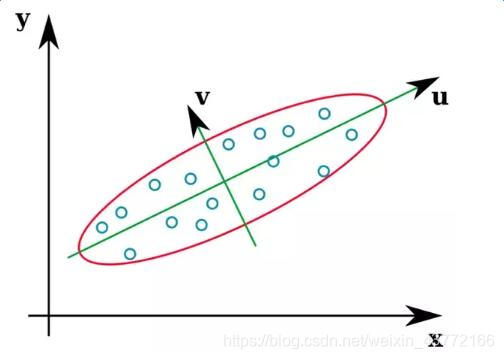
每个数据样本都是可以用坐标x、y表示的二维点。这些数据样本的协方差矩阵的特征向量是u和v。较长的u是第一特征向量,较短的v是第二特征向量。特征值的大小用箭头的长度表示。
我们可以看到,第一个特征向量(从数据的平均值)指向欧几里德空间中数据方差最大的方向,第二个特征向量跟第一特征向量是垂直的。
三维空间中的特征向量就比较复杂,如图所示:
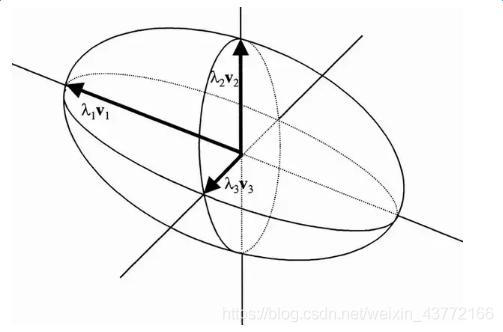
我们假设所有的数据点都在椭圆体内。v1是第一特征向量,λ1是其相应的特征值,指向数据方差最大的方向。v2与v1垂直,是这个方向上数据方差最大的特征向量。v3与v1和v2都垂直,是这个方向上数据方差最大的特征向量,虽然只有这一个方向。