目录
findpeaks函数的功能是寻找局部最大值。
语法
pks = findpeaks(data)
[pks,locs] = findpeaks(data)
[pks,locs,w,p] = findpeaks(data)
[___] = findpeaks(data,x)
[___] = findpeaks(data,Fs)
[___] = findpeaks(___,Name,Value)
findpeaks(___)
说明
pks = findpeaks(data)
返回带有输入信号向量data的局部最大值(峰值)的向量。局部峰值是大于其两个相邻样本或等于Inf的数据样本。峰值按出现的顺序输出。不包括非Inf信号端点。如果峰是平的,函数只返回指数最低的点。
[pks,locs] = findpeaks(data)
还会返回峰值出现的索引。
[pks,locs,w,p] = findpeaks(data)
还返回峰的宽度作为向量w,峰的突出度作为向量p。
[___] = findpeaks(data,x)
将x指定为位置向量,并返回以前语法中的任何输出参数。loc和w用x表示。
[___] = findpeaks(data,Fs)
指定数据的采样速率Fs。假设第一个数据样本是在时间零点采集的。loc和w转换为时间单位。
[___] = find peaks(_ _ _,Name,Value)
指定使用名称-值参数以及以前语法中的任何输入参数的选项。
不带输出参数的findpeaks(___)绘制信号并覆盖峰值。
示例
寻找向量中的峰值
定义一个有三个峰值的矢量并画出来。
data = [25 8 15 5 6 10 10 3 1 20 7];
plot(data)如图所示:
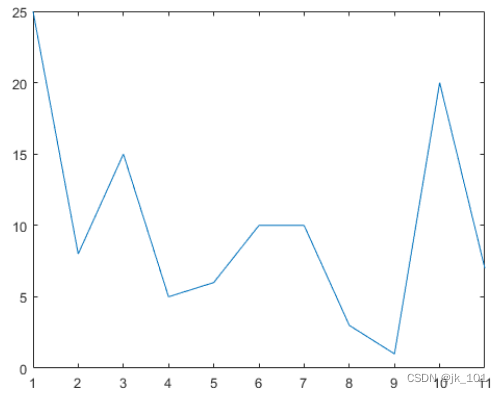
求局部极大值。峰值按出现的顺序输出。第一个样本不包括在内,尽管它是最大值。对于平峰,该函数仅返回指数最低的点。
pks = findpeaks(data)
pks = 1×3
15 10 20
使用不带输出参数的findpeaks来显示峰值。
findpeaks(data)如图所示:
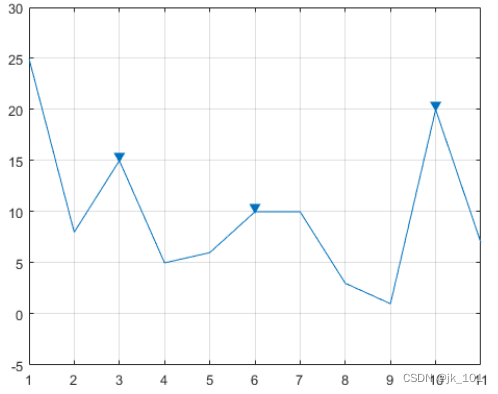
查找峰值及其位置
创建一个由一系列钟形曲线组成的信号。指定每条曲线的位置、高度和宽度。
x = linspace(0,1,1000);
Pos = [1 2 3 5 7 8]/10;
Hgt = [3 4 4 2 2 3];
Wdt = [2 6 3 3 4 6]/100;
for n = 1:length(Pos)
Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2);
end
PeakSig = sum(Gauss);画出各条曲线及其总和。
plot(x,Gauss,'--',x,PeakSig)如图所示:
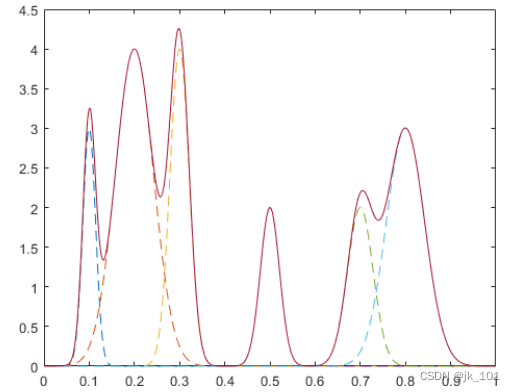
使用默认设置的findpeaks查找信号的峰值及其位置。
[pks,locs] = findpeaks(PeakSig,x);使用findpeaks绘制峰并标记它们。
findpeaks(PeakSig,x)
text(locs+.02,pks,num2str((1:numel(pks))'))如图所示:
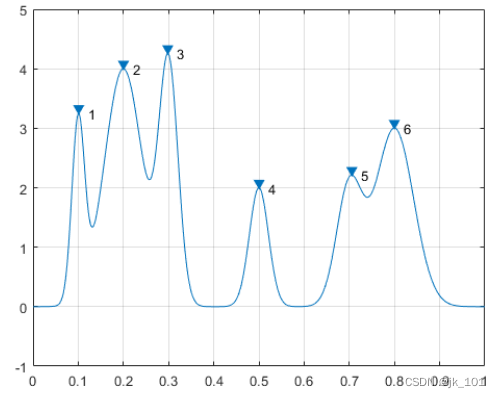
从最高到最低对山峰进行排序。
[psor,lsor] = findpeaks(PeakSig,x,'SortStr','descend');
findpeaks(PeakSig,x)
text(lsor+.02,psor,num2str((1:numel(psor))'))如图所示:
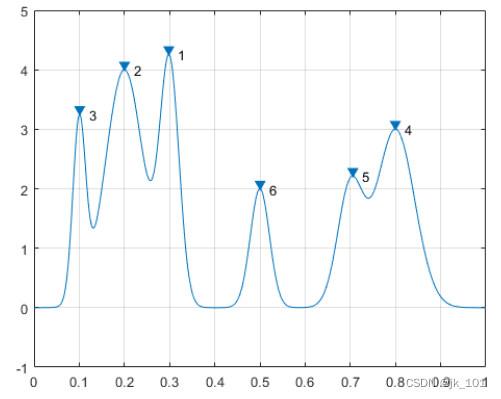
峰值突起
创建一个信号,该信号由一个完整余弦周期上的钟形曲线之和组成。指定每条曲线的位置、高度和宽度。
x = linspace(0,1,1000);
base = 4*cos(2*pi*x);
Pos = [1 2 3 5 7 8]/10;
Hgt = [3 7 5 5 4 5];
Wdt = [1 3 3 4 2 3]/100;
for n = 1:length(Pos)
Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2);
end
PeakSig = sum(Gauss)+base;画出各条曲线及其总和。
plot(x,Gauss,'--',x,PeakSig,x,base)如图所示:
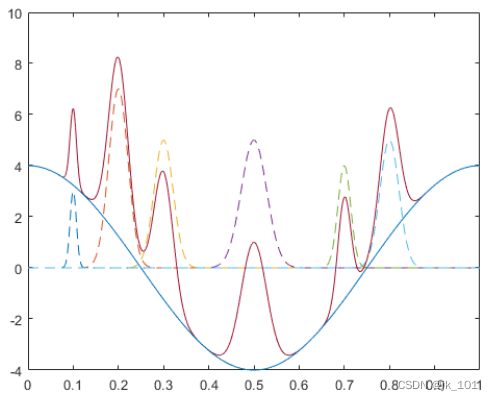
使用findpeaks定位并绘制显著度至少为4的峰。
findpeaks(PeakSig,x,'MinPeakProminence',4,'Annotate','extents')如图所示:
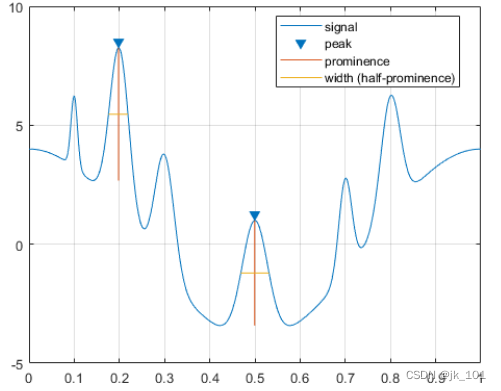
只有最高和最低的峰值满足该条件。 显示所有峰的日珥和半日珥宽度。
[pks,locs,widths,proms] = findpeaks(PeakSig,x);
widths
widths = 1×6
0.0154 0.0431 0.0377 0.0625 0.0274 0.0409
proms
proms = 1×6
2.6816 5.5773 3.1448 4.4171 2.9191 3.6363
寻找分离度最小的峰
太阳黑子是一种循环现象。已知它们的数量大约每11年达到一个峰值。 加载文件spocitizen . dat,其中包含了从1700年到1987年每年观测到的太阳黑子的平均数量。找到并画出最大值。
load sunspot.dat
year = sunspot(:,1);
avSpots = sunspot(:,2);
findpeaks(avSpots,year)如图所示:
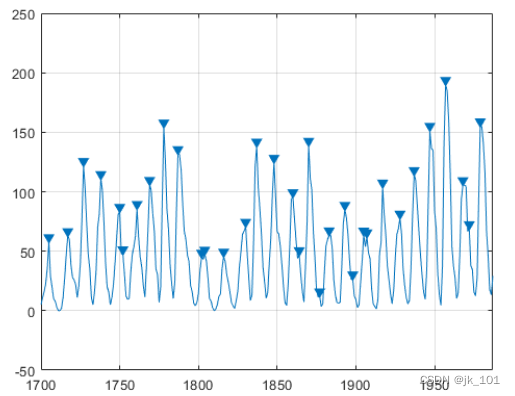
通过忽略彼此非常接近的峰值来改进对周期持续时间的估计。再次查找并绘制峰,但现在将可接受的峰-峰分离限制为大于6年的值。
findpeaks(avSpots,year,'MinPeakDistance',6)如图所示:
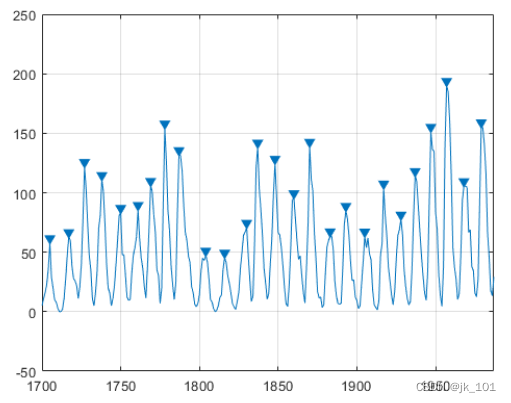
使用findpeaks返回的峰位置来计算最大值之间的平均间隔。
[pks,locs] = findpeaks(avSpots,year,'MinPeakDistance',6);
meanCycle = mean(diff(locs))
meanCycle = 10.9600使用年份数据创建日期时间数组。假设太阳黑子在每年的3月20日被计数,接近春分。找出太阳黑子的高峰期。使用年数函数将最小峰间距指定为持续时间。
ty = datetime(year,3,20);
[pk,lk] = findpeaks(avSpots,ty,'MinPeakDistance',years(6));
plot(ty,avSpots,lk,pk,'o')如图所示:
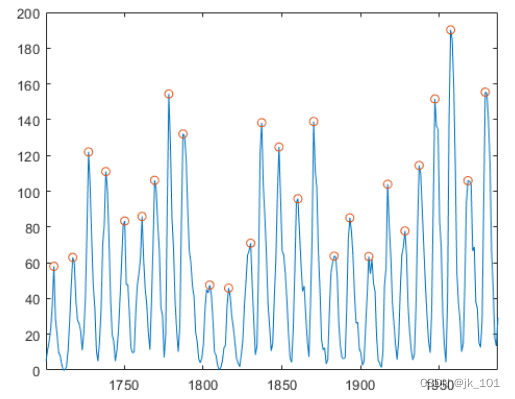
使用日期时间函数计算平均太阳黑子周期。
dttmCycle = years(mean(diff(lk)))
dttmCycle = 10.9600用这些数据创建一个时间表。以年为单位指定时间变量。绘制数据。显示时间表的最后五个条目。
TT = timetable(years(year),avSpots);
plot(TT.Time,TT.Variables)如图所示:
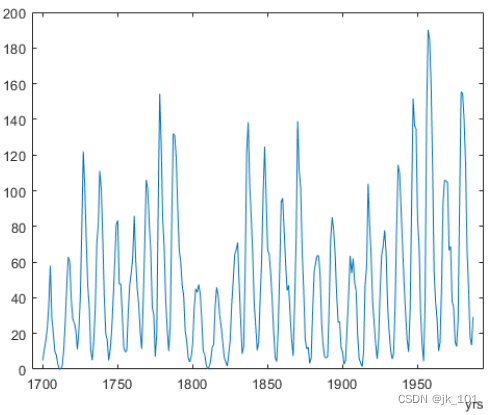
entries = TT(end-4:end,:)
entries=5×1 timetable
Time avSpots
________ _______
1983 yrs 66.6
1984 yrs 45.9
1985 yrs 17.9
1986 yrs 13.4
1987 yrs 29.3
约束峰值特征
加载以7418 Hz采样的音频信号。选择200个样本。
load mtlb
select = mtlb(1001:1200);找出间隔至少5 ms的峰。 要应用此约束,findpeaks会选择信号中最高的峰值,并消除其5毫秒内的所有峰值。然后,该函数对最高的剩余峰重复该过程,并进行迭代,直到用完要考虑的峰。
findpeaks(select,Fs,'MinPeakDistance',0.005)如图所示:
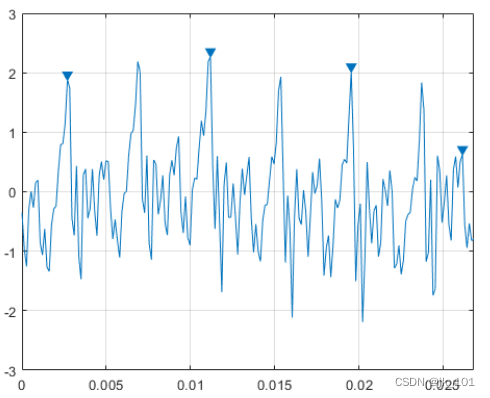
找出幅度至少为1 V的峰值。
findpeaks(select,Fs,'MinPeakHeight',1)如图所示:
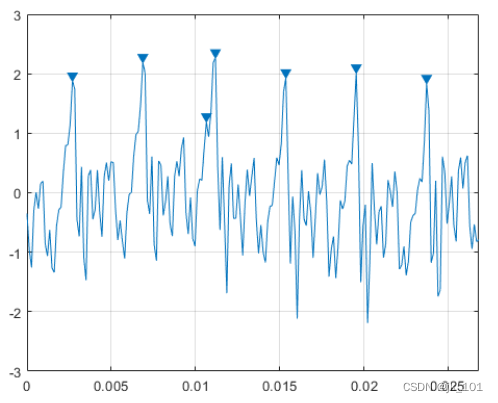
找出比相邻样本至少高1 V的峰值。
findpeaks(select,Fs,'Threshold',1)如图所示:
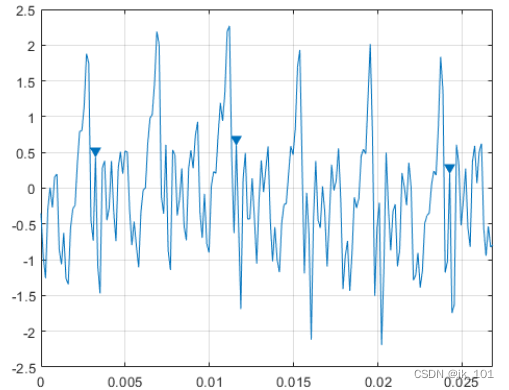
在信号达到更高值之前,找出任一侧下降至少1 V的峰值。
findpeaks(select,Fs,'MinPeakProminence',1)如图所示:
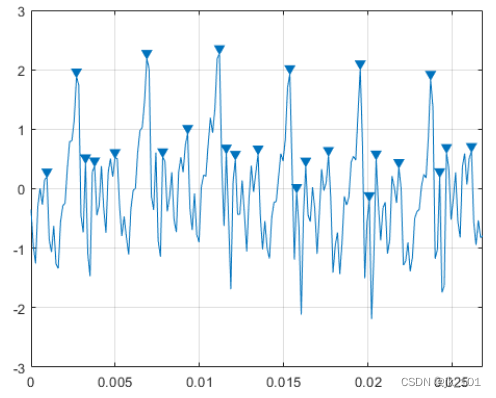
饱和信号的峰值
如果数据大于给定的饱和点,传感器可以返回削波读数。可以选择忽略这些没有意义的峰值,或者将它们纳入您的分析中。 产生一个信号,该信号由嵌入方差为0.1的高斯白噪声中的频率为5 Hz和3 Hz的三角函数的乘积组成。信号以100 Hz的速率采样一秒钟。重置随机数生成器以获得可重现的结果。
rng default
fs = 1e2;
t = 0:1/fs:1-1/fs;
s = sin(2*pi*5*t).*sin(2*pi*3*t)+randn(size(t))/10;通过截断每个大于指定界限0.32的读数来模拟饱和测量。绘制饱和信号。
bnd = 0.32;
s(s>bnd) = bnd;
plot(t,s)
xlabel('Time (s)')如图所示:
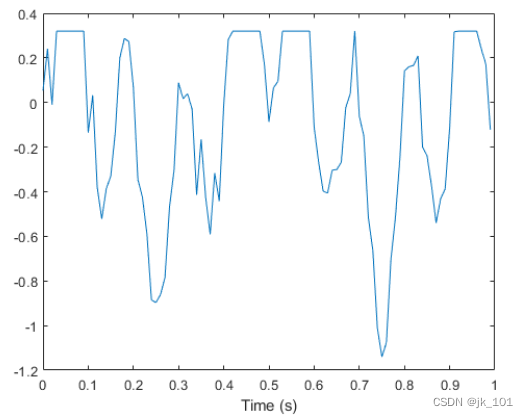
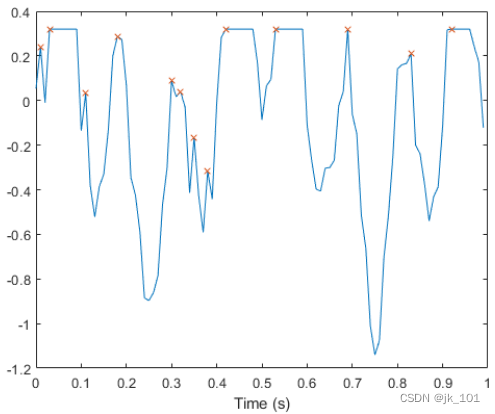
找到信号的峰值。findpeaks只报告每个平峰的上升沿。
[pk,lc] = findpeaks(s,t);
hold on
plot(lc,pk,'x')如图所示:
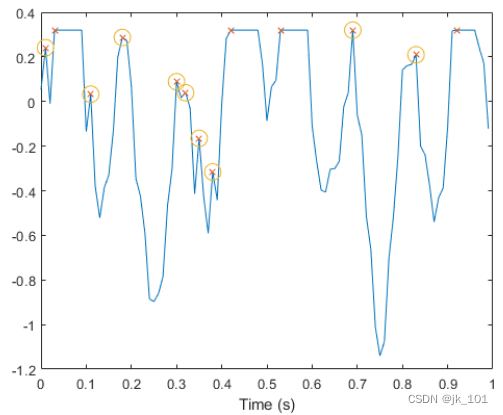
使用“阈值”名称-值对来排除平峰。要求最小幅度差为10^-4 一座山峰和它的邻居之间。
[pkt,lct] = findpeaks(s,t,'Threshold',1e-4);
plot(lct,pkt,'o','MarkerSize',12)如图所示:
确定峰宽
创建一个由一系列钟形曲线组成的信号。指定每条曲线的位置、高度和宽度。
x = linspace(0,1,1000);
Pos = [1 2 3 5 7 8]/10;
Hgt = [4 4 2 2 2 3];
Wdt = [3 8 4 3 4 6]/100;
for n = 1:length(Pos)
Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2);
end
PeakSig = sum(Gauss);画出各条曲线及其总和。
plot(x,Gauss,'--',x,PeakSig)
grid如图所示:
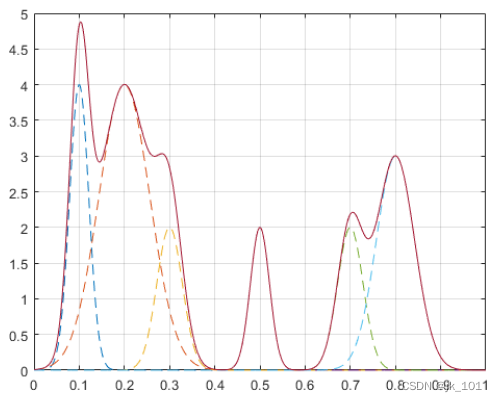
使用半日珥作为参考测量峰的宽度。
findpeaks(PeakSig,x,'Annotate','extents')如图所示:
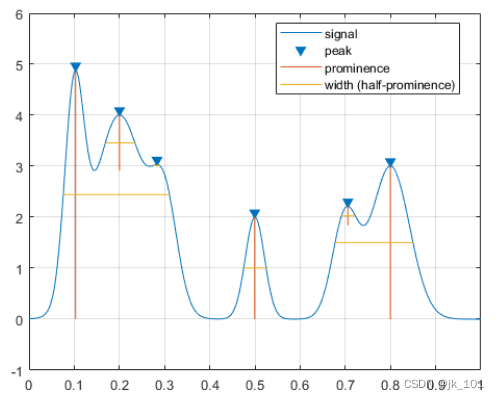
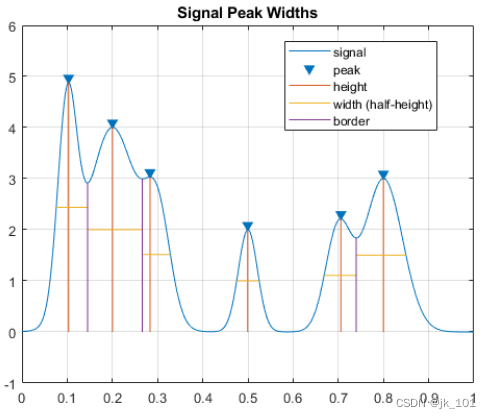
再次测量宽度,这次使用一半高度作为参考。
findpeaks(PeakSig,x,'Annotate','extents','WidthReference','halfheight')
title('Signal Peak Widths')如图所示: