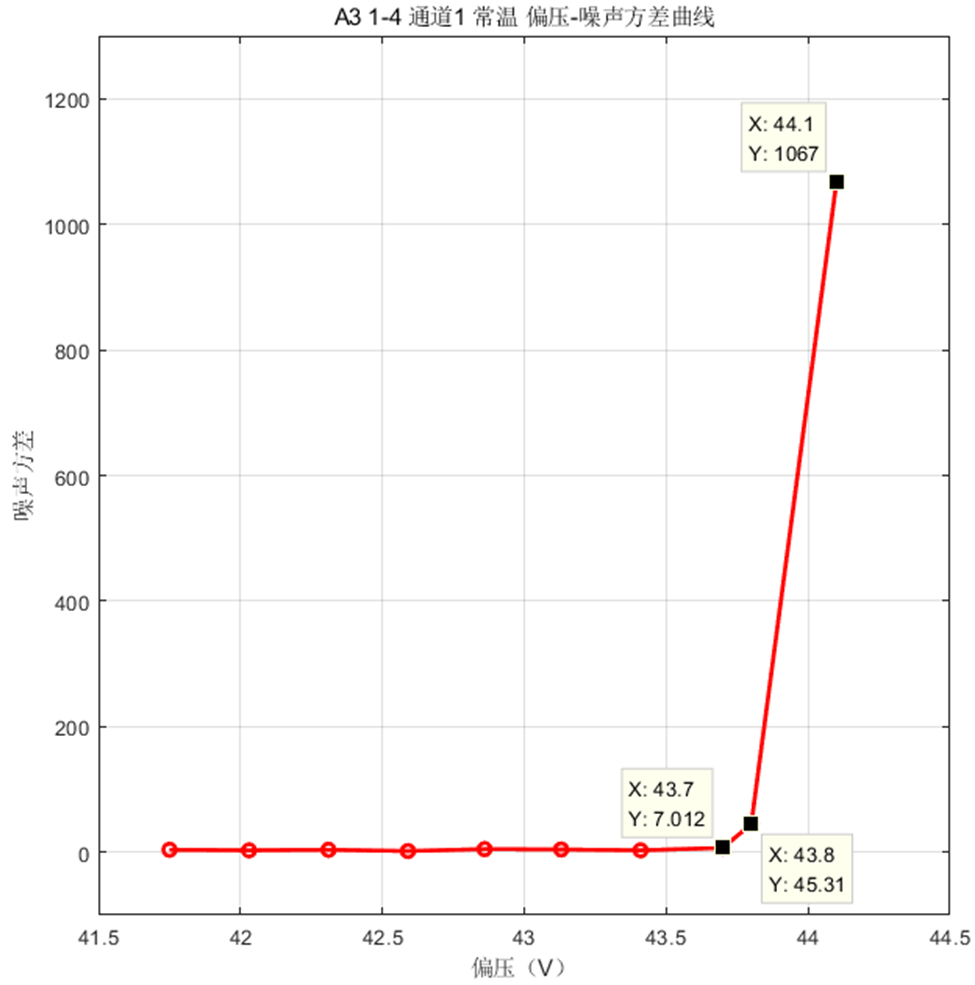
测距器件APD的性能与器件本身的温度、施加在APD的偏置电压息息相关。 在不同的温度下，APD的偏压对测距性能的影响非常大。 要确定一个合适的APD的偏压Vopt，首先你要知道当前温度下，APD的击穿电压Vbr，一般来讲，Vopt = Vbr – ΔV，ΔV基本是个固定的值。如果要使用算法找到Vbr，通过寻找APD采集信号的噪声方差的

剧变

点去寻找Vbr是一个不错的方式。 如下图所示，当方差从10以下，突然剧变到45.31，信号噪声方差剧变4倍不止。我们就可以定义此处偏压43.8V为击穿电压Vbr。 那么要在FPGA实现此功能，首先需要在FPGA中实现方差的计算，这也是本文的内容。

这算是脱离例程，第一个本人自己设计的FPGA小模块。

1 CSDN C知道

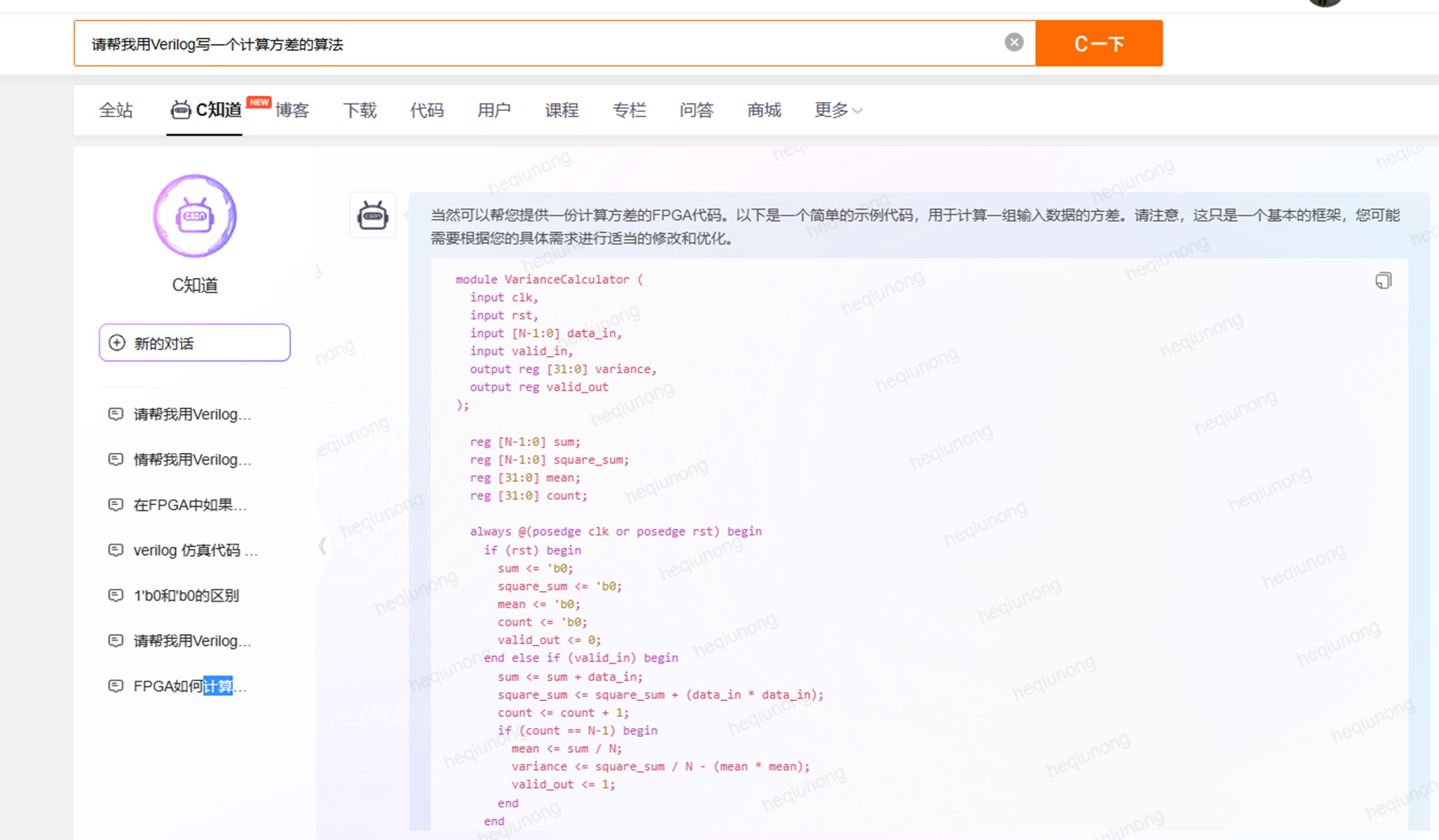
ChatGPT已经火爆的不行了，猪如何在ChatGPT的风口起飞，这个问题还真是为难。 不过使用ChatGPT倒是不难，CSDN推出了基于ChatGPT的C知道，功能还是比较强大的。我也赶一下时髦，我对C知道问了一个问题：请帮我用Verilog写一个计算方差的算法。

module VarianceCalculator (
  input clk,
  input rst,
  input [N-1:0] data_in,
  input valid_in,
  output reg [31:0] variance,
  output reg valid_out
);

  reg [N-1:0] sum;
  reg [N-1:0] square_sum;
  reg [31:0] mean;
  reg [31:0] count;

  always @(posedge clk or posedge rst) begin
    if (rst) begin
      sum <= 'b0;
      square_sum <= 'b0;
      mean <= 'b0;
      count <= 'b0;
      valid_out <= 0;
    end else if (valid_in) begin
      sum <= sum + data_in;
      square_sum <= square_sum + (data_in * data_in);
      count <= count + 1;
      if (count == N-1) begin
        mean <= sum / N;
        variance <= square_sum / N - (mean * mean);
        valid_out <= 1;
      end
    end
  end

endmodule

从算法上来讲，计算方差倒不是一个很难的问题，比如用平方的均值减去均值的平方（平方的期望减去期望的平方）。 C知道提供的Verilog代码就是这样算的，是没有问题的。 但直接拿来用，还是存在少许问题。 不过C知道已经很强大了，是很有参考价值的。

2 V1.0 纯时序逻辑实现

我已记不清从哪里接受了一个写Verilog代码的观念，就是：

一个时序逻辑（


always


块），只写一个变量

。这样做的好处是，修改调试非常方便，可以根据仿真结果看哪个变量有问题，然后我就专门去修改那个变量对应的时序逻辑。 不过坏处是，它不如全部变量写到一个时序逻辑里面那样，一眼看到算法的全貌。不过，我不管它的坏处是啥，总之这是我接受的观念，也是我后续编写FPGA代码的风格和态度。

下面给出，我用

纯时序逻辑写的

方差计算FPGA代码。

2.1 Verilog代码

`timescale 1ns / 1ps

module VarCalculatorV1(
        input   wire            clk             ,
        input   wire            rst_n           ,
        input   wire    [7:0]   data_in         ,
        input   wire            valid_in        ,
        output  reg     [15:0]  variance        ,
        output  reg             valid_out
);

//==================================================================
//                        Parameter define
//==================================================================
parameter       N = 256;

//==================================================================
//                        Internal Signals
//==================================================================
reg     [31:0]  count;
reg     [15:0]  sum;
reg     [31:0]  square_sum;
reg     [7:0]   mean;

//----------------------------- valid_out -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                valid_out <= 1'b0;     
        end
        else if (count == N+1)begin
                valid_out <= 1'b1;
        end
        else begin
                valid_out <= 1'b0;
        end
end

//----------------------------- variance -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                variance <= 'd0;     
        end
        else if (valid_in==1'b1 && count >= N+1 )begin
                variance <= (square_sum >> 8) - (mean * mean);
        end
        else begin
                variance <= 'd0;
        end
end

//----------------------------- count -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                count <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N+2) begin
                        count <= 'd0;
                end
                else begin
                        count <= count + 1'b1;
                end
        end
        else begin
                count <= 'd0;
        end
end

//----------------------------- sum -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                sum <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count < N) begin
                        sum <= sum + data_in;
                end
                else if(count == N || count == N+1) begin
                        sum <= sum;
                end
                else if(count == N+2) begin
                        sum <= 'd0;
                end
        end
        else begin
                sum <= 'd0;
        end
end


//----------------------------- square_sum -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                square_sum <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count < N) begin
                        square_sum <= square_sum + data_in*data_in;
                end
                else if(count == N || count == N+1) begin
                        square_sum <= square_sum;
                end
                else if(count == N+2) begin
                        square_sum <= 'd0;
                end
        end
        else begin
                square_sum <= 'd0;
        end
end


//----------------------------- mean -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                mean <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count >= N) begin
                        mean <= sum >> 8;
                end
                else begin
                        mean  <= 'd0;
                end
        end
        else begin
                sum <= 'd0;
        end
end


endmodule

啰嗦几句废话哈，由于需要验证代码的准确性，因此我们对其进行了ModelSim仿真。 本来呢，由于ModelSim的仿真代码我不是很熟悉， 我还不太会使用仿真代码来创建一个我想要的data_in。所以，我在仿真的时候，在用到data_in的地方，我都是用模块内部的计数变量count来代替的。（也就是说，我们计算的是从0~255这256个数的方差）。后来仿真成功确定了代码的准确性之后，我重新去调整我的仿真代码，使得我给到这个模块的data_in变量和模块内部的count变量是一样的。

下面给出对应的ModelSim仿真代码。

2.2 ModelSim仿真代码

`timescale 1ns/1ps
module tb_VarCalculator (); /* this is automatically generated */

    // clock
    reg clk;
    reg rst_n;
    reg  [7:0] data_in;
    reg        valid_in;
    wire [15:0] variance;
    wire        valid_out;

    parameter N = 256;

    VarCalculatorV1 #(
            .N(N)
        ) inst_VarCalculator (
            .clk       (clk),
            .rst_n     (rst_n),
            .data_in   (data_in),
            .valid_in  (valid_in),
            .variance  (variance),
            .valid_out (valid_out)
        );

    initial begin
        clk <= 1'b0;
        forever #(10) clk = ~clk;
    end

    initial begin
        rst_n <= 1'b0;
        #10
        rst_n <= 1'b1;
    end

    initial begin
        valid_in <= 1'b0;
        #10
        valid_in <= 1'b1;
    end

    
    reg [15:0] tb_count;
    initial begin
        tb_count <= 'd0;
        data_in <= 'd0;
        #10
        // 仿真代码中for循环是比较值得后续学习参考的
        for(tb_count = 1; tb_count <= N+3; tb_count = tb_count + 1) begin
            #20
            if(tb_count<='d255) begin
                data_in <= tb_count; 
            end
            else begin
                if (tb_count=='d258) begin
                    tb_count <= 'd0;
                end
                data_in <= 'd0; 
            end                
        end
    end

endmodule

仿真的时候，有个小技巧，真的好方便，特别提高仿真效率。

2.3 高效仿真小技巧

首先找到如下图所示的仿真

编译

文件 tb_VarCalculator_compile.do。

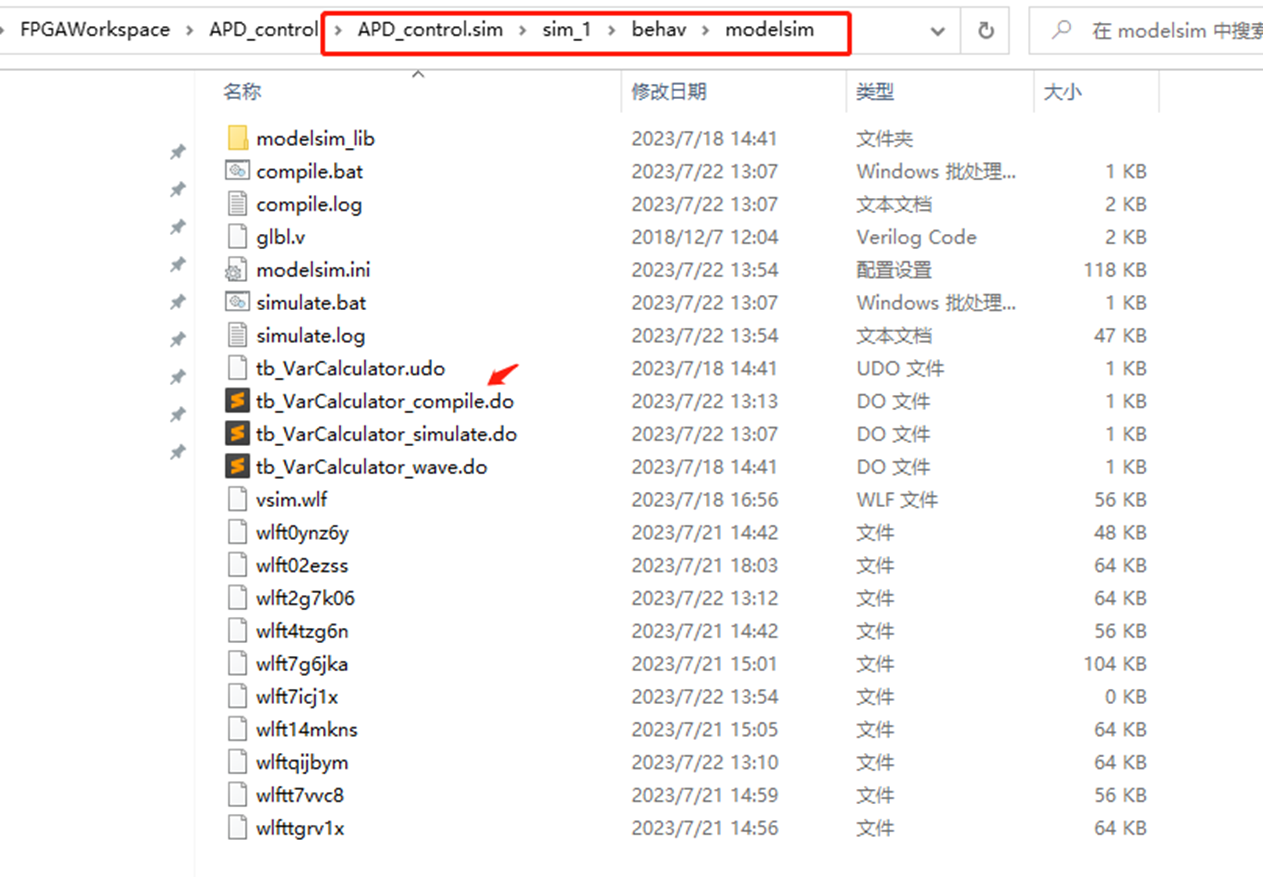
打开这个文件，注释最后一行。

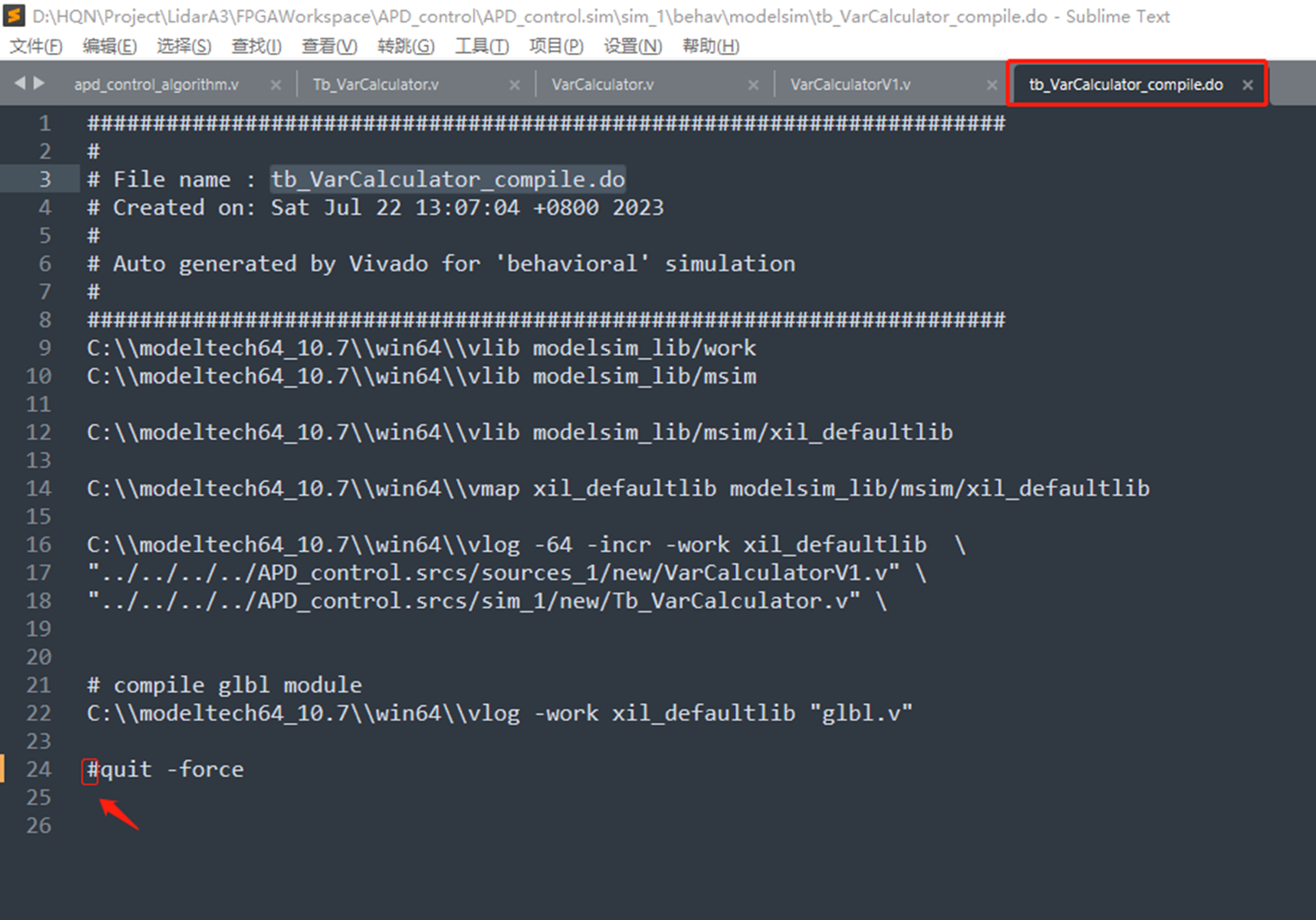
修改完这个编译文件后， 后续你如果你的仿真代码或者你的功能模块代码有任何的改动，你改了之后先保存。

然后在ModelSim命令行输入三个命令（第一次输入后，后面你用上键↑下键↓就能快速输入了），

编译 → 重启 → 运行。

就可以实现快速修改代码仿真。

2.4 仿真结果

分析一下仿真结果

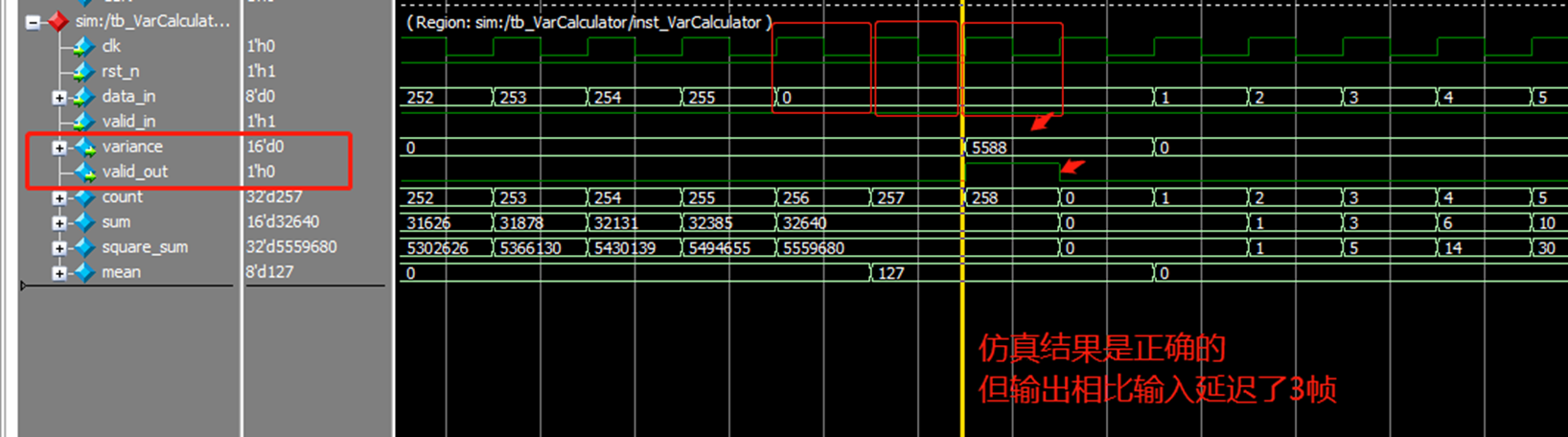
1、可以看到仿真代码给出的data_in在0~255部分是和咱们模块内部的count变量一模一样的。仿真代码里面的for循环还是有点东西的，相信以后的仿真肯定可以借鉴。

2、仿真结果5588也是非常接近咱们用MatLAB算的0~255的方差的。 不能完全相等的原因是，我们的数据量个数是2^8，所以我们的除法是用的位移运算实现的。肯定会存在一定的误差。

3、咱们方差的计算结果延迟的3帧，

1 首先时序逻辑肯定是要延迟1帧的，所以我在求所有数据的和、求所有数据的平方和的时候，就已经延迟了1帧。

2 其次，得到所有数据的和之后，我计算了所有数据的均值，这里又延迟了一帧。

3 最后，在得到所有数据的均值之后，我又求了所有数据的平方和的均值 减去 均值的平方。

因此咱们总共延迟了三帧。 甚至我都担心最后一步在一个时钟周期内算不过来，还能再进行拆分，不过呢，这样延迟更多了，可能变成4帧或者5帧的。

这个很多帧延迟经常让人难以接受，所以我们下面用组合逻辑进行优化。

3 V2.0 时序逻辑+组合逻辑

组合逻辑是没有时钟延迟的。

当我用时序逻辑，求了所有数据的和，以及所有数据的平方和之后（延迟1帧）。

我可以用组合逻辑，就在当前时钟周期，立即得到：均值、均值的平方、平方和的均值、以及用平方和的均值减去均值的平方得到方差。

那么最终得到的方差，也只会延迟1帧。

3.1 Verilog代码

`timescale 1ns / 1ps

module VarCalculator(
        input   wire            clk      ,
        input   wire            rst_n    ,
        input   wire    [7:0]   data_in ,
        input   wire            valid_in,
        output  wire    [15:0]  variance,
        output  reg             valid_out
);

//==================================================================
//                        Parameter define
//==================================================================
parameter       N = 256;

//==================================================================
//                        Internal Signals
//==================================================================
reg     [31:0]  count;
reg     [15:0]  sum;
reg     [31:0]  square_sum;
wire    [7:0]   mean;
wire    [23:0]  square_mean;
wire    [15:0]  mean_square;

// 🔺 组合逻辑，优化延迟
assign square_mean = square_sum >> 8;
assign mean_square = mean * mean;
assign variance = ( valid_in==1'b1 && count == N ) ? (square_mean - mean_square) : 'd0;
assign mean = (valid_in==1'b1 && count == N) ? (sum >> 8) : 'd0;

//----------------------------- valid_out -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                valid_out <= 1'b0;     
        end
        else if (count == N-1)begin
                valid_out <= 1'b1;
        end
        else begin
                valid_out <= 1'b0;
        end
end

//----------------------------- count -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                count <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        count <= 'd0;
                end
                else begin
                        count <= count + 1'b1;
                end
        end
        else begin
                count <= 'd0;
        end
end


//----------------------------- sum -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                sum <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        sum <= 'd0;                       
                end
                else begin
                        sum <= sum + data_in;
                end
        end
        else begin
                sum <= 'd0;
        end
end


//----------------------------- square_sum -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                square_sum <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        square_sum <= 'd0;                     
                end
                else begin
                        square_sum <= square_sum + data_in*data_in;
                end
        end
        else begin
                square_sum <= 'd0;
        end
end

endmodule

3.2 仿真结果

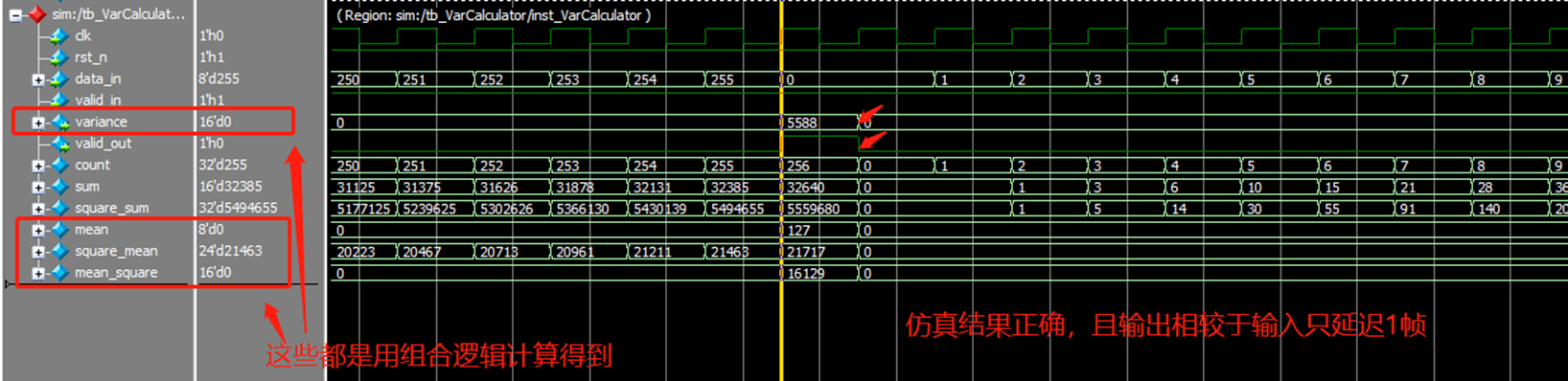
从仿真结果可看出，方差计算仍然正确，但是延迟只有1帧。 另外，其实咱们的verilog代码也要比V1.0版本精简一些。

4 V3.0 组合逻辑部分的优化（考虑位宽对输出结果的影响）

在组合逻辑的计算部分，变量的位宽存在一些小问题，进行进一步优化。

`timescale 1ns / 1ps

module var_compute(
        input   wire            clk,
        input   wire            rst_n,
        input   wire    [7:0]   data_in,
        input   wire            valid_in,
        output  wire    [15:0]  variance,
        output  reg             valid_out
);

//==================================================================
//                        Parameter define
//==================================================================
parameter       N = 256;

//==================================================================
//                        Internal Signals
//==================================================================
reg     [31:0]  count;
reg     [15:0]  sum;
reg     [23:0]  square_sum;    // 🔺 修改
wire    [7:0]   mean;
wire    [15:0]  square_mean;    // 🔺 修改        
wire    [15:0]  mean_square;


assign square_mean = square_sum[23-:16];    // 🔺 修改
assign mean_square = mean * mean;
assign variance = ( (valid_in==1'b1) && (count == N) && (square_mean > mean_square) ) ? (square_mean - mean_square) : 'd0;    // 🔺 修改
assign mean = (valid_in==1'b1 && count == N) ? sum[15-:8] : 'd0;    // 🔺 修改

//----------------------------- valid_out -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                valid_out <= 1'b0;     
        end
        else if (count == (N-1) )begin
                valid_out <= 1'b1;
        end
        else begin
                valid_out <= 1'b0;
        end
end

//----------------------------- count -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                count <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        count <= 'd0;
                end
                else begin
                        count <= count + 1'b1;
                end
        end
        else begin
                count <= 'd0;
        end
end


//----------------------------- sum -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                sum <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        sum <= 'd0;                       
                end
                else begin
                        sum <= sum + data_in;
                end
        end
        else begin
                sum <= 'd0;
        end
end


//----------------------------- square_sum -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                square_sum <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        square_sum <= 'd0;                     
                end
                else begin
                        square_sum <= square_sum + data_in*data_in;
                end
        end
        else begin
                square_sum <= 'd0;
        end
end

endmodule

5 V4.0  算法精度优化

我们在求均值的时候用sum右移8位求均值，会损失一定的精度。 然后用已经损失过精度求得的均值去平方，得到期望的平方→E^2(x)，再一次损失精度。   如果我先把sum平方，在除以N^2，即右移16位，以这样的方式来得到期望的平方→E^2(x)，精度的损失会比以前的方式小很多。 基于此思路，我们做了进一步的优化。代码如下。

`timescale 1ns / 1ps

module var_compute(
        input   wire            clk,
        input   wire            rst_n,
        input   wire    [7:0]   data_in,
        input   wire            valid_in,
        output  wire    [15:0]  variance,
        output  reg             valid_out
);

//==================================================================
//                        Parameter define
//==================================================================
parameter       N = 256;

//==================================================================
//                        Internal Signals
//==================================================================
reg     [31:0]  count;
(* MARK_DEBUG="true" *) reg     [15:0]  sum;
(* MARK_DEBUG="true" *) reg     [23:0]  square_sum;
(* MARK_DEBUG="true" *) wire    [7:0]   mean;
(* MARK_DEBUG="true" *) wire    [15:0]  square_mean;
(* MARK_DEBUG="true" *) wire    [15:0]  mean_square;
(* MARK_DEBUG="true" *) wire    [31:0]  sum_square;    // 🔺修改

assign sum_square       = (valid_in==1'b1 && count == N) ? (sum*sum) : 'd0; // 🔺修改
assign mean_square      = sum_square[31-:16]; // 🔺修改
assign square_mean      = square_sum[23-:16];
assign variance = ( (valid_in==1'b1) && (count == N) && (square_mean > mean_square) ) ? (square_mean - mean_square) : 'd0;

//----------------------------- valid_out -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                valid_out <= 1'b0;     
        end
        else if (count == (N-1) )begin
                valid_out <= 1'b1;
        end
        else begin
                valid_out <= 1'b0;
        end
end

//----------------------------- count -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                count <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        count <= 'd0;
                end
                else begin
                        count <= count + 1'b1;
                end
        end
        else begin
                count <= 'd0;
        end
end


//----------------------------- sum -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                sum <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        sum <= 'd0;                       
                end
                else begin
                        sum <= sum + data_in;
                end
        end
        else begin
                sum <= 'd0;
        end
end


//----------------------------- square_sum -----------------------------
always @(posedge clk or negedge rst_n) begin
        if (rst_n == 1'b0) begin
                square_sum <= 'd0;     
        end
        else if (valid_in==1'b1)begin
                if (count == N) begin
                        square_sum <= 'd0;                     
                end
                else begin
                        square_sum <= square_sum + data_in*data_in;
                end
        end
        else begin
                square_sum <= 'd0;
        end
end

endmodule

本文之所得：

0、C知道的代码不能是直接用的，只能参考，别想偷懒。

1、ModelSim高效仿真小技巧（其实在前面的博文已经强调过一次，再次强调一遍，真的很高效）

2、一个时序逻辑模块里面，尽量只给一个变量赋值。

3、用组合逻辑可以优化时序逻辑的延迟。

4、组合逻辑的运算一定要注意

位宽匹配

的问题。

5、验证算法同时还要考虑

精度问题

。