1.0 无障碍,右下走,代价相等
m*n的方格,要求最短路径从左上角到右下角,有多少种走法(有多少条最短路径)?

解法一:
动态规划,
因为是最短路径,所以每一步只能往右或者往下走
,那么到第n步(不在第一行或者第一列)只有两种方式:从上往下来的,或者左往右来的。
所以可设二维数组:dp[m][n],dp[i][j]即从入口(a[0][0])走到a[i][j]的最短路径数目,容易推知:
状态方程:
dp[i][j] = dp[i][j-1] + dp[i-1][j]
边界条件:
dp[0][j] 和 dp[i][0]
代码很容易写出来:
int[][] dp = new int[m][n]; // 自动赋值0
//第一行第一列,边界条件
for(int i = 0; i < n; i++)
dp[0][i] = 1;
for(int i = 1; i < m; i++) // dp[0][0]已经赋过值
dp[i][0] = 1;
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++)
dp[i][j] = dp[i][j-1]+dp[i-1][j];
}
return dp[m-1][n-1]l;
解法二:
再看这个图:

其实要最快走到出口,必然要往右走n步,往下走m步,总共要走m+n步。同样地,如果一个走法向走了n步,向下走了m步,那么该走法的路径一定是一条最短路径。
即:往右走n步,往下走m步和最短路径是充分必要条件。
再回到问题,对于路途中的当前步,想往下走(m步没有用完的前提下),还是往右走(n步没有用完的前提下)都是任意的。但是,
如果确定了哪些步往右走,则往下走的步数也确定了
,如下图:
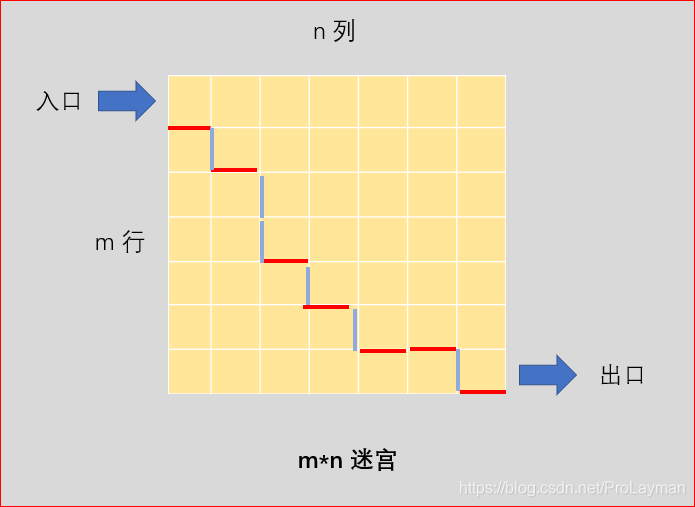
红色(往右走)确定了以后,蓝色自然就确定了。即在m+n步中选好了那些步往右(共n步),剩下的都是往下。
这就是数学中的组合问题(not排列),eg:给m+n个球上色(球标号1~m+n):只能上黑色或者白色,有多少种着色法。
所以问题变成从m+n步中挑出n/m步:
或者
:
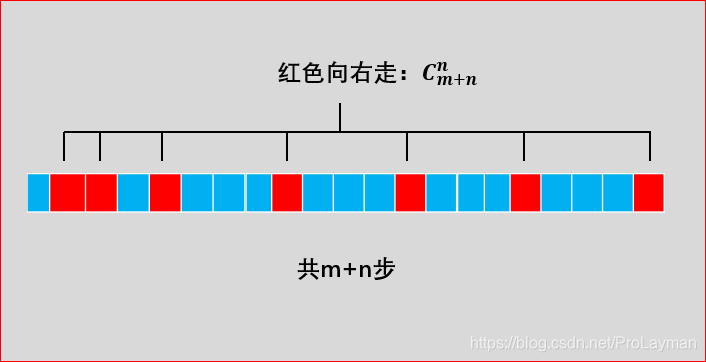
代码完全是计算
或者
的问题:
(高中数学知识)
PS:
是排列(有顺序),
是组合(无顺序)
上代码:
int count = 1;
for(int i = m+n; i > 0; i--){
if(i > n)
count *= i;
else
count /= i;
}
return count;
变式:有障碍,右下走,代价相等
m*n的方格,只能往右或者往下走,其中有一些格子不能走,用值-1表示,其余的格子可以走,用值1表示,现在要求最短路径从左上角到右下角,有多少种走法(有多少条最短路径)?

这个只是在边界初始化和迭代计算状态方程时加上判断条件即可,并且障碍物的
看代码:
int[][] dp = new int[m][n]; // 自动赋值0
//第一行第一列,边界条件
for(int i = 0; i < n; i++){
if(1 == a[0][i])
dp[0][i] = 1;
else
break; // 后面都是默认的0值(0条路径)
}
for(int i = 0; i < m; i++){
if(1 == a[i][0])
dp[i][0] = 1;
else
break; // 后面都是默认的0值(0条路径)
}
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
if(1 == a[i][0]) // 障碍物的dp不计算,还是默认的0,不影响
dp[i][j] = dp[i][j-1]+dp[i-1][j];
}
}
return dp[m-1][n-1]l;
网上也有其他解析:
2.0 无障碍,右下走,代价不等
m*n的方格,要求
只能往右走或者往下走
,从左上角到右下角的最短路径是多少?
题目示例:
leetcode 64. 最小路径和
如图:
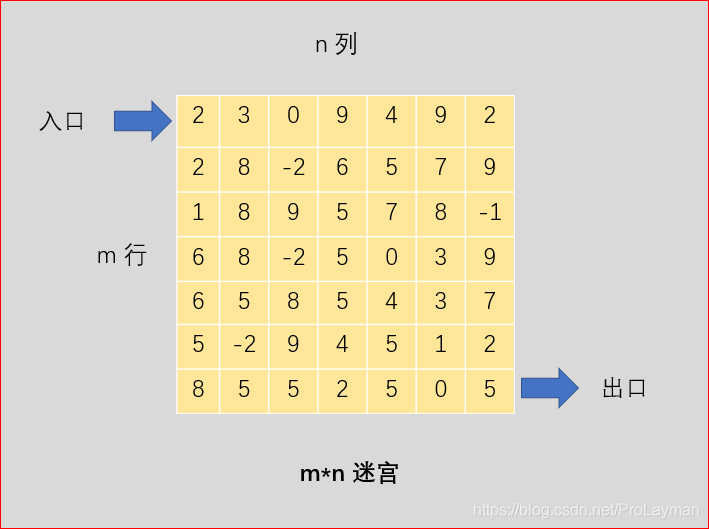
解答:
思路:还是使用dp,只是状态方程和边界条件变了:
可设二维数组:dp[m][n],dp[i][j]即从入口(a[0][0])走到a[i][j]的最短路径数目,容易推知:
状态方程:dp[i][j] = min(dp[i][j-1] + dp[i-1][j]) + a[i][j]
边界条件:本题dp[0][j] 和 dp[i][0] 成了前n项和的问题(因为只有一种走法:将第一行/列前面的全部走完)
代码很容易写出来:
int[][] dp = new int[m][n]; // 自动赋值0
//第一行第一列,边界条件
dp[0][0] = a[0][0];
for(int i = 1; i < n; i++) // dp[0][0]已赋值
dp[0][i] = dp[0][i-1]+a[0][i]; // 迭代求和
for(int i = 1; i < m; i++)
dp[i][0] = dp[i-1][0]+a[i][0];
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++)
dp[i][j] = Math.min(dp[i][j-1],dp[i-1][j])+a[i][j]; // Math.min有多个重载方法,有int的
}
return dp[m-1][n-1]l;也可见:
给定一个矩阵m,从左上角开始每次只能向右走或者向下走,最后达到右下角的位置
由于右下走比较简单,可以引入负代价:
变式:
无障碍,右下走,代价不等并可能为负值
题目示例:
leetcode
174. 地下城游戏
策略为
自顶而下的动态规划
。
参考1.0由无障碍到有障碍的变式,本题也有:
变式:有障碍,右下走,代价不等(大于0)
m*n的方格,只能往右或者往下走,其中有一些格子不能走,用值-1表示,其余的格子可以走,且代价不等(均不等于-1且小于等于10000),求从左上角到右下角的最短路径
是多少
?
参考1.0的引入障碍后的变式:
① 第一行第一列只要碰到障碍,包括障碍在内的后面格子dp均是0(0条路径)
② 剩余的格子,从dp[1][1]开始,按照从左到右,从上往下的顺序,计算dp[i][j]。只有当前不是障碍时,才使用
dp[i][j] = dp[i][j-1] + dp[i-1][j]
若是障碍,则不处理(默认值为0)
本题是计算最小路径的大小,不是计算有多少条,则对应到上题,本题策略应该为:
① 第一行第一列采用累加策略(只有这一条路可走)计算dp,只要碰到障碍,包括障碍在内的后面格子dp均是
正无穷
② 剩余的格子,从dp[1][1]开始,按照从左到右,从上往下的顺序,计算dp[i][j]。只有当前不是障碍时,才使用
dp[i][j] = min(dp[i][j-1] + dp[i-1][j])+a[i][j]
若是障碍,则赋值
正无穷
代码:
int[][] dp = new int[m][n]; // 自动赋值0
//第一行第一列,边界条件
dp[0][0] = a[0][0];
for(int i = 1; i < n; i++){
if(-1 != a[0][i])
dp[0][i] = dp[0][i-1]+a[0][i]; // 迭代求和
else{
for(int j = i; j < n; j++)
dp[0][i] = Integer.MAX_VALUE; // Integer.MAX_VALUE来表示正无穷
}
}
for(int i = 1; i < m; i++){
if(-1 != a[i][0])
dp[i][0] = dp[i-1][0]+a[i][0];
else{
for(int j = i; j < m; j++)
dp[i][0] = Integer.MAX_VALUE;
}
}
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
if(-1 != a[i][0])
dp[i][j] = Math.min(dp[i][j-1],dp[i-1][j])+a[i][j];
else
dp[i][j] = Integer.MAX_VALUE; // Integer.MAX_VALUE来表示正无穷
}
}
return dp[m-1][n-1]l;
3.0 有障碍,任意走,代价相等(大于等于0)
即一般性迷宫问题
m*n的方格,要求从左上角到右下角,可以上下左右走,但不能斜着走,1代表可以走,-1代表障碍物,求最短路径(保证有唯一解)?e.g.
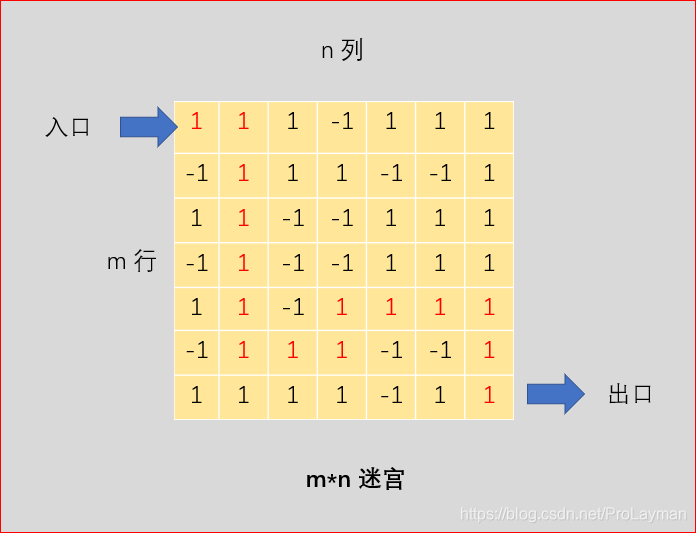
其实就是最基础的图的最短路径问题,而本题是代价相同的图最短路径:
解法很经典:DFS或BFS
DFS做的:
BFS做的:
练习的话可以看Leetcode
1091. 二进制矩阵中的最短路径
还有:
4.0 有障碍,任意走,代价不等(大于等于0)
即一般性的图最短路径问题
图最短路径问题最“暴力”的解法就是BFS和DFS,只是相对3.0,本题的每步代价不一样,代码改动倒很小:
dp[i][j]更新时的条件由 XXX 改为 XXX。
它的变式很多,一个更为简单的变式就是:
变式:无障碍,任意走,代价不等
即没有障碍的迷宫,其实以图的视角看,就是联通度更高的图而已,方法都是和上面的一样,甚至还简单些,不用判断是不是障碍。
当然,图的最短路径是个大学问,Dijkstra算法,plim算法,Flord算法
如果引入负权边,还有其他算法。(2,0虽然有负权边,但是只能右下走,dp一直取了最小值,没有使用DFS和BFS,故没有问题)
大学问,大学问啊。