误差来源的两个方面:
bias(偏差)
:度量了某种学习算法的平均估计结果所逼近的学习目标的程度。
variance(方差)
:度量了在面对同样规模的不同训练集时分散的程度。
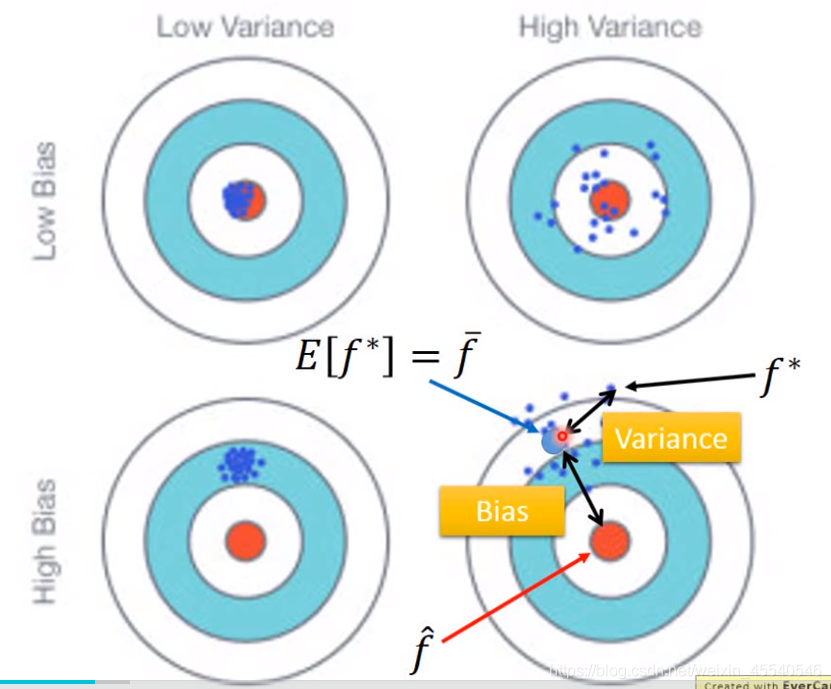
高的bias表示离目标值远,低bias表示离靶心近;高的variance表示多次学习的结果越分散,低的variance表示多次学习的结果越集中。
区别
variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。
bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度。
先看没有bias存在的情况

图中的N个点他们的平均值不等μ,但是当取值足够多,它的期望与μ相等。比喻就是,没有bias就是说瞄准的是靶心没有偏差,但是射击的时候由于一些因素,实际射击的位置散落在了μ的周围。
不同训练集分散的程度取决于variance:

怎么估测variance:

当N足够大时,s方的期望才会等于variance。
例子比喻
不同的f*是不同训练集的原因
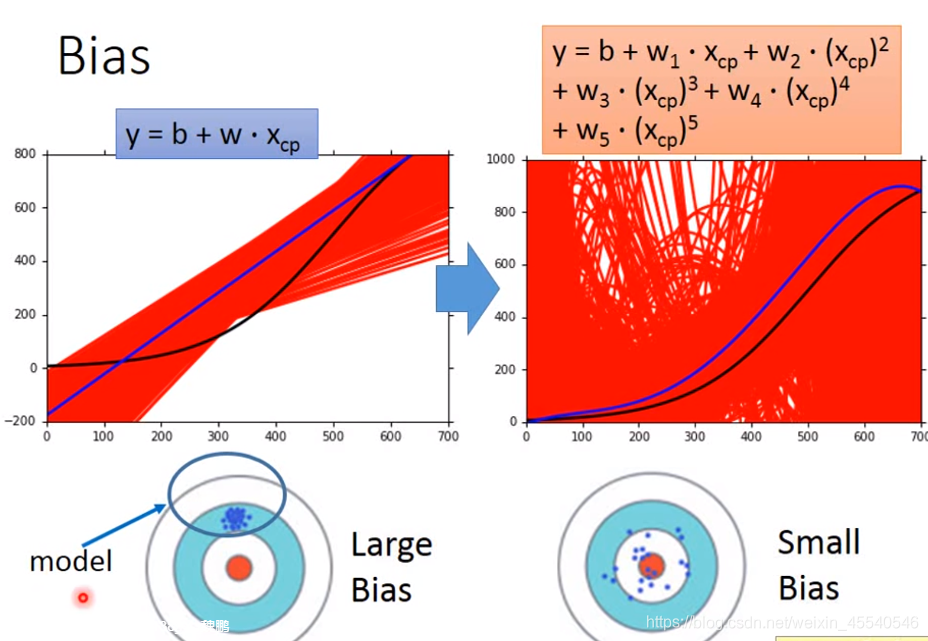
简单的模型往往对应着比较大的bias,复杂的模型往往对应着较小的bias.
bias和variance
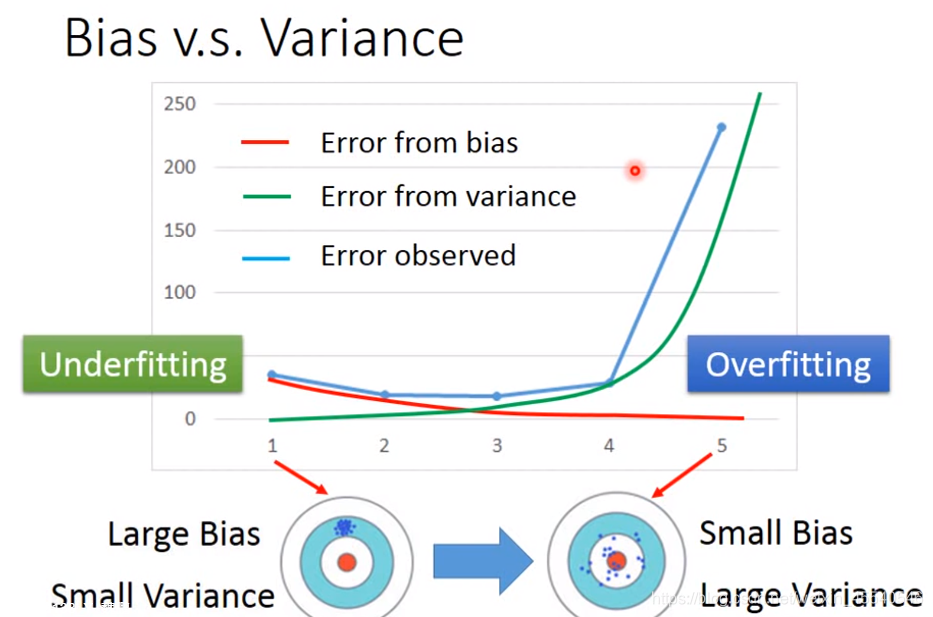
可以看出随着模型逐渐复杂,bias逐渐变小,variance逐渐变大。bias大,variance小的情况意味着欠拟合;bias小,variance大的情况意味着过拟合。
对于较大的bias怎么进行处理:
如果模型无法fit训练集代表bias比较大,即欠拟合。
如果模型在训练集表现好,在测试集表现较差,则属于过拟合。

对于bias较大处理方法:
1、加入更多的feature
2、设计更加复杂的模型
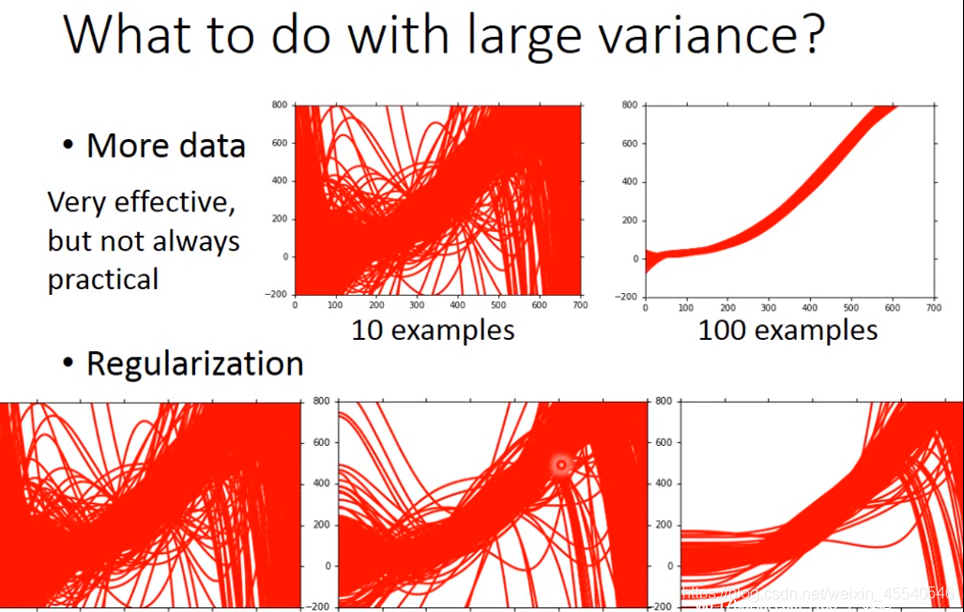
对于较大的variance怎么进行处理:
1、增加数据(非常有效,但是不太实际)
2、正则化(regularization)(需要调节bias和variance之间的平衡关系)
怎么进行模型选择
用拥有的测试集上的准确率最好的模型,应用于实际场合中,效果不一定好

如何防止上述情况:
cross validation(交叉验证):

N折交叉验证
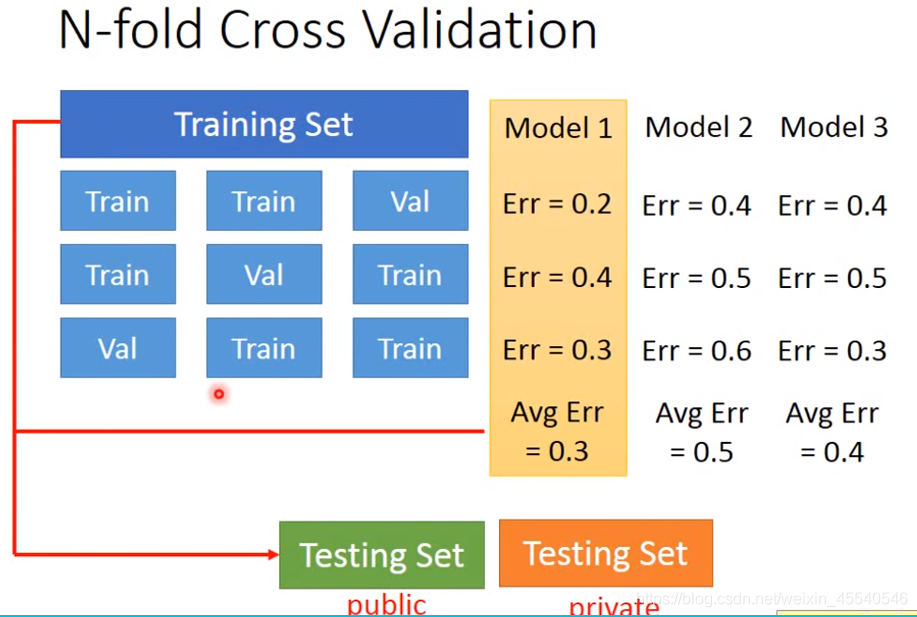
对模型进行交叉验证,选出平均错误率最低的模型,然后利用此模型对所有的样本重训练。