一、ADF检验

在使用很多时间序列模型的时候，如 ARMA、ARIMA，都会要求时间序列是平稳的，所以一般在研究一段时间序列的时候，第一步都需要进行平稳性检验，除了用肉眼检测的方法，另外比较常用的严格的统计检验方法就是ADF检验，也叫做单位根检验。

ADF检验全称是 Augmented Dickey-Fuller test，顾名思义，ADF是 Dickey-Fuller检验的增广形式。DF检验只能应用于一阶情况，当序列存在高阶的滞后相关时，可以使用ADF检验，所以说ADF是对DF检验的扩展。

二、单位根

一阶AR模型，即AR(1)的情况，其模型如下：



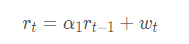
如果α1 = 1 ，成为单位根。该模型就是随机游走，我们知道它是不平稳的。换个思路想象一下，当α1 = 1 ，那么前一时刻的收益率对当下时刻的影响是100%的，不会减弱；那么就算是很远的某个时刻，当下对它的影响还是不会消除，所以方差（表现在波动）是受前面所有时刻的影响，是和 t 相关的，因此不平稳；

如果α1 > 1，那么当前时刻的波动不仅受前面时刻的影响，还被放大了，所以肯定不平稳；

只有当α1 < 1 的时候，前面时刻的波动对当前时刻的影响会逐渐减小。可以计算此时的自协方差以及自相关系数是一个固定值。所以这种情况下，序列是平稳的。

三、ADF检验的原理

ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

所以，ADF检验的 H0 假设就是存在单位根，如果得到的显著性检验统计量小于三个置信度（10%，5%，1%），则对应有（90%，95%，99%）的把握来拒绝原假设。

四、ADF检验的python实现

ADF检验可以通过python中的 statsmodels 模块，这个模块提供了很多统计模型。

1.引入库

代码如下：

from statsmodels.tsa.stattools import adfuller

2.函数说明

adfuller函数的参数意义分别是：

1. x：一维的数据序列。
2. maxlag：最大滞后数目。
3. regression：回归中的包含项（c：只有常数项，默认；ct：常数项和趋势项；ctt：常数项，线性二次项；nc：没有常数项和趋势项）。
4. autolag：自动选择滞后数目（AIC：赤池信息准则，默认；BIC：贝叶斯信息准则；t-stat：基于maxlag，从maxlag开始并删除一个滞后直到最后一个滞后长度基于 t-statistic 显著性小于5%为止；None：使用maxlag指定的滞后）。
5. store：True False，默认。
6. regresults：True 完整的回归结果将返回。False，默认。

返回值意义为：

1. adf：Test statistic，T检验，假设检验值。
2. pvalue：假设检验结果。
3. usedlag：使用的滞后阶数。
4. nobs：用于ADF回归和计算临界值用到的观测值数目。
5. icbest：如果autolag不是None的话，返回最大的信息准则值。
6. resstore：将结果合并为一个dummy。

五、时间序列分析

1.使用IH2112股指期货数据为例

2.使用IH2112股指期货数据为例

    result = adfuller(ih_df["IH2112"].values)
    print(result)

3. 将数据进行一阶差分滞后

    ih_df_diff = np.diff(ih_df["IH2112"].values)
    result = adfuller(ih_df_diff)
    print(result)