

1)梯度下降θθ的更新过程,走梯度方向的反方向:




Sigmoid
函数求导:
函数:f(z) = 1 / (1 + exp( − z))
导数:f(z)’ = f(z)(1 − f(z))
求导过程如下:

softmax的损失函数:
对于给定的测试输入

,我们想用假设函数针对每一个类别j估算出概率值
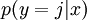
。也就是说,我们想估计

的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个

维的向量(向量元素的和为1)来表示这

个估计的概率值。 具体地说,我们的假设函数
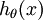
形式如下:
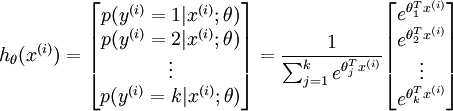
其中
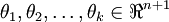
是模型的参数。请注意
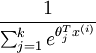
这一项对概率分布进行归一化,使得所有概率之和为 1
代价函数
现在我们来介绍 softmax 回归算法的代价函数。在下面的公式中,
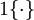
是示性函数,其取值规则为:
值为真的表达式
,
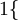
值为假的表达式
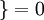
。举例来说,表达式
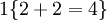
的值为1 ,
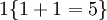
的值为 0。我们的代价函数为:
![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/7/6/3/7634eb3b08dc003aa4591a95824d4fbd.png)
值得注意的是,上述公式是logistic回归代价函数的推广。logistic回归代价函数可以改为:
![\begin{align}J(\theta) &= -\frac{1}{m} \left[ \sum_{i=1}^m (1-y^{(i)}) \log (1-h_\theta(x^{(i)})) + y^{(i)} \log h_\theta(x^{(i)}) \right] \\&= - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=0}^{1} 1\left\{y^{(i)} = j\right\} \log p(y^{(i)} = j | x^{(i)} ; \theta) \right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/5/4/9/5491271f19161f8ea6a6b2a82c83fc3a.png)
可以看到,Softmax代价函数与logistic 代价函数在形式上非常类似,只是在Softmax损失函数中对类标记的

个可能值进行了累加。注意在Softmax回归中将

分类为类别

的概率为:
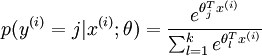
.
对于

的最小化问题,目前还没有闭式解法。因此,我们使用迭代的优化算法(例如梯度下降法,或 L-BFGS)。经过求导,我们得到梯度公式如下:
![\begin{align}\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} \left( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) \right) \right] }\end{align}](http://ufldl.stanford.edu/wiki/images/math/5/9/e/59ef406cef112eb75e54808b560587c9.png)
让我们来回顾一下符号 ”
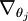
” 的含义。
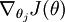
本身是一个向量,它的第

个元素
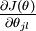
是

对

的第

个分量的偏导数。
有了上面的偏导数公式以后,我们就可以将它代入到梯度下降法等算法中,来最小化

。 例如,在梯度下降法的标准实现中,每一次迭代需要进行如下更新:
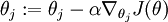
(
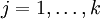
)。
其中
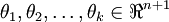
是模型的参数。请注意
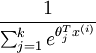
这一项对概率分布进行归一化,使得所有概率之和为 1
1)线性回归要求变量服从正态分布,logistic回归对变量分布没有要求。
2)线性回归要求因变量是连续性数值变量,而logistic回归要求因变量是分类型变量。
3)线性回归要求自变量和因变量呈线性关系,而logistic回归不要求自变量和因变量呈线性关系
4)logistic回归是分析因变量取某个值的概率与自变量的关系,而线性回归是直接分析因变量与自变量的关系
softmax is a generalization of logistic function that “squashes”(maps) a K-dimensional vector z of arbitrary real values to a K-dimensional vector σ(z) of real values in the range (0, 1) that add up to 1.
sigmoid将一个real value映射到(0,1)的区间,用来做二分类。
而 softmax 把一个 k 维的real value向量(a1,a2,a3,a4….)映射成一个(b1,b2,b3,b4….)其中 bi 是一个 0~1 的常数,输出神经元之和为 1.0,所以相当于概率值,然后可以根据 bi 的概率大小来进行多分类的任务。
二分类问题时 sigmoid 和 softmax 是一样的,求的都是 cross entropy loss,而 softmax 可以用于多分类问题
softmax是sigmoid的扩展,因为,当类别数 k=2 时,softmax 回归退化为 logistic 回归。具体地说,当 k=2 时,softmax 回归的假设函数为:

利用softmax回归参数冗余的特点,从两个参数向量中都减去向量θ1 ,得到:

最后,用 θ′ 来表示 θ2−θ1,上述公式可以表示为 softmax 回归器预测其中一个类别的概率为

另一个类别概率的为

这与 logistic回归是一致的。
softmax建模使用的分布是多项式分布,而logistic则基于伯努利分布
多个logistic回归通过叠加也同样可以实现多分类的效果,但是 softmax回归进行的多分类,类与类之间是互斥的,即一个输入只能被归为一类;多个logistic回归进行多分类,输出的类别并不是互斥的,即”苹果”这个词语既属于”水果”类也属于”3C”类别。
LR 损失函数为什么用极大似然函数?
-
因为我们想要让 每一个 样本的预测都要得到最大的概率,
即将所有的样本预测后的概率进行相乘都最大,也就是极大似然函数. -
对极大似然函数取对数以后相当于对数损失函数,
由上面 梯度更新 的公式可以看出,
对数损失函数的训练求解参数的速度是比较快的,
而且更新速度只和x,y有关,比较的稳定, -
为什么不用平方损失函数
如果使用平方损失函数,梯度更新的速度会和 sigmod 函数的梯度相关,sigmod 函数在定义域内的梯度都不大于0.25,导致训练速度会非常慢。
而且平方损失会导致损失函数是 theta 的非凸函数,不利于求解,因为非凸函数存在很多局部最优解
均方误差和交叉熵损失函数比较
一.前言
在做神经网络的训练学习过程中,一开始,经常是喜欢用二次代价函数来做损失函数,因为比较通俗易懂,后面在大部分的项目实践中却很少用到二次代价函数作为损失函数,而是用交叉熵作为损失函数。为什么?一直在思考这个问题,这两者有什么区别,那个更好?下面通过数学的角度来解释下。
思考:
1.我们希望我们损失函数能够做到,当我们预测的值跟目标值越远时,在修改参数时候,减去一个更大的值,做到更加快速的下降。
2.哪个函数更不容易陷入局部最优解
二.两种代价函数的表达式
二次代价损失函数:
![]()
交叉熵损失函数:
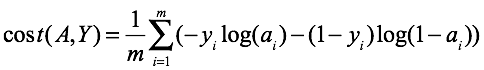
针对二分类来说,其中:
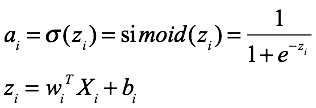
ai第Xi个样本经过前向传播之后到达最后一个节点的值
三.收敛速度比较
两个函数反向传播梯度比较
1.二次代价函数
为了方便只取一个样本,那么损失为:

那么w,b的梯度为:
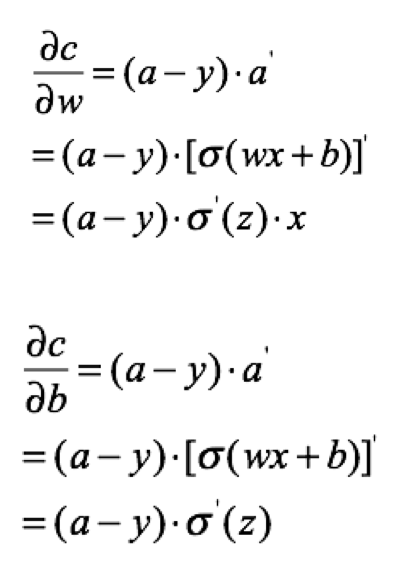
2.交叉熵
为了方便只取一个样本,损失为:
![]()
计算w,b的梯度:

分析和结论
由此可看出,在做后向传播时
1.对于square mean在更新w,b时候,w,b的梯度跟激活函数的梯度成正比,激活函数梯度越大,w,b调整就越快,训练收敛就越快,但是Simoid函数在值非常高时候,梯度是很小的,比较平缓。
2.对于cross entropy在更新w,b时候,w,b的梯度跟激活函数的梯度没有关系了,bz已经表抵消掉了,其中bz-y表示的是预测值跟实际值差距,如果差距越大,那么w,b调整就越快,收敛就越快。