B. 减成一
题目描述
存在n个数,每次操作可以任选一个区间使得区间内的所有数字减一。问最少多少次操作,可以让所有数都变成1.
Solution
情况1
:如果num[i] >= num[i – 1],num[i]被减到1,num[i – 1]一定也可以在num[i]的部分操作中减到1。即如果数列递增,num[n]减到1的操作数即为答案。
情况2
:如果num[i] < num[i – 1],则如果对num[i]操作,num[i – 1]要到1还得补上(num[i – 1] – num[i])次操作,则最终答案就是需要补上的操作和+num[n]减到1的方案数。
题解
:把原数组转化为差分数组,则转化为将差分数组转化为1 0 0 0 0…的方案数。最快操作方式就是将差分数组第一个数减为1,其余减为0。即操作数为差分数组的正数之和减一。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//__builtin_popcount(n);
#define IOS ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
#define RI register int
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int SZ = 2e5 + 10;
int n;
int num[SZ];
int main()
{
int T;
scanf("%d",&T);
while(T --)
{
scanf("%d",&n);
int ans = 0;
for(int i = 1;i <= n;i ++)
{
scanf("%d",&num[i]);
ans += max(num[i - 1] - num[i],0);
}
ans += num[n] - 1;
printf("%d\n",ans);
}
return 0;
}
C. 面积
题目大意
如图所示,正方形周围接4个半圆,求图形的面积
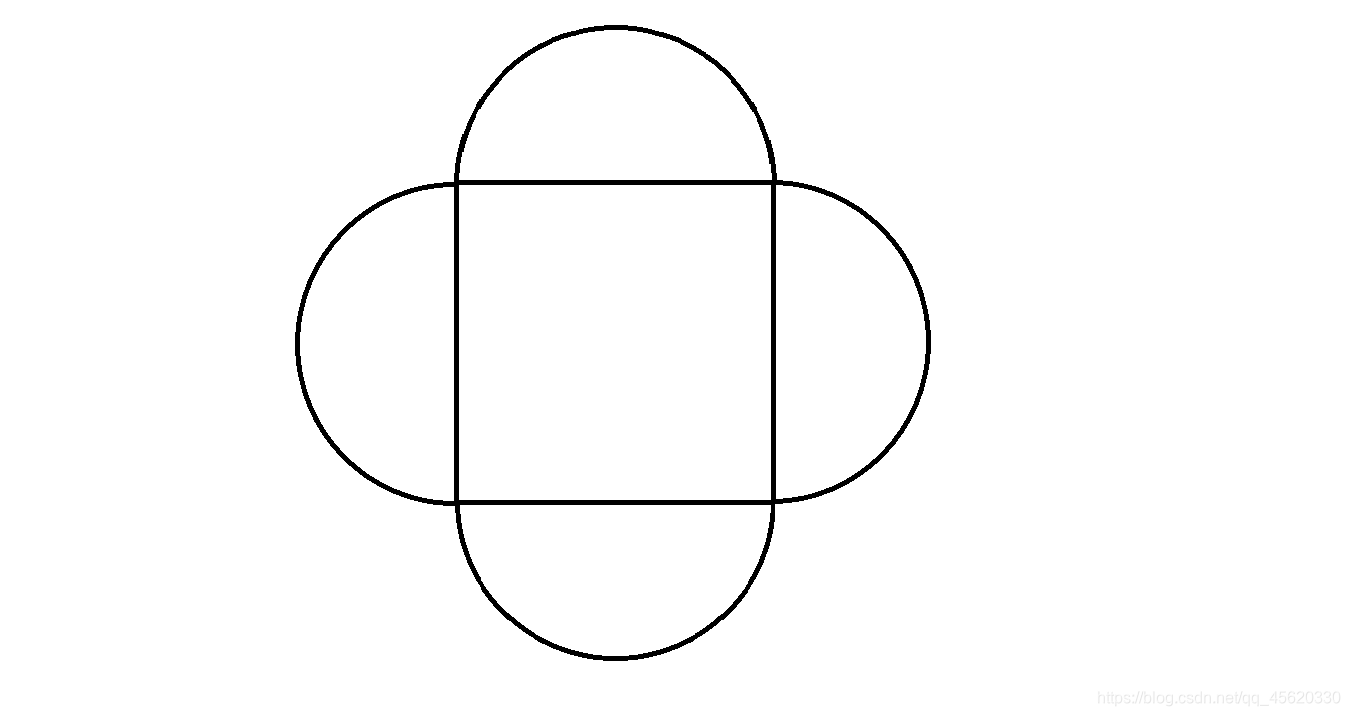
Solution
签到,注意要求即可。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//__builtin_popcount(n);
#define IOS ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
#define RI register int
const int MOD = 1e9 + 7;
const double PI = 3.14;
const int INF = 0x3f3f3f3f;
const int SZ = 2e5 + 10;
int x;
int main()
{
int T;
scanf("%d",&T);
while(T --)
{
scanf("%d",&x);
double ans = x * x + 2 * PI * ((double)(x * x) / 4.0);
printf("%.2lf\n",ans);
}
return 0;
}
D.扔硬币
题目描述
有n枚硬币,每枚硬币扔出来是正面和反面的概率各占50%。小明同时扔下了n枚硬币后,已知至少有m枚硬币是反面。请问恰好有k枚硬币是正面的概率是多少。答案对1e9取模。
Solution
公式:
C(n,k)/ (2^n – ΣC(n,i) ) (0 <= i < m)
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int SZ = 600000 + 10;
const ll MOD = 1e9 + 7;
ll n,m,p,k;
ll JC[SZ];
inline ll pow_mod(ll a,ll b,ll c)
{
ll r = 1;
while(b)
{
if(b & 1) r = (r * a) % c;
a = (a * a) % c;
b >>= 1;
}
return r;
}
inline ll C(ll n,ll m)
{
if(m > n) return 0;
return ((JC[n] * pow_mod(JC[m],p - 2,p)) % p * pow_mod(JC[n - m],p - 2,p) % p);
}
/*
inline ll Lucas(ll n,ll m)
{
if(!m) return 1;
return C(n % p,m % p) * Lucas(n / p, m / p) % p;
}
*/
inline void get_JC()
{
JC[0] = 1;
for(int i = 1;i <= 100010;i ++) JC[i] = (JC[i - 1] * i) % p;
}
int main()
{
p = MOD;
get_JC();
int T;
scanf("%d",&T);
while(T--)
{
scanf("%lld%lld%lld",&n,&m,&k);//p为大质数
if(n < m + k) {printf("0\n");continue;}
ll sum = pow_mod(2,n,p);
for(int i = 0;i < m;i ++)
sum = (sum - C(n,i) + MOD) % MOD;
ll ans = (C(n,k) * pow_mod(sum,p - 2,p)) % MOD;
printf("%lld\n",ans);
}
}
E.赛马
题目描述
一天小明与他同学准备赛马,他们每人有n匹马,每匹马有一个固定的战力值,战力值高的马会战胜战力值低的马并赢得比赛。每匹马只能出场比赛一次。小明偷看到了他对手每匹马的出场顺序,小明在更改自己马出场顺序后最多能赢多少场比赛。
Solution
贪心,出场顺序没有意义,将两人的马排序,用小明的当前最强马去打对手可战胜的最强马,这样可以为以后的马留下更多可战胜马。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//__builtin_popcount(n);
#define IOS ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
#define RI register int
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int SZ = 2e5 + 10;
int n;
int a[SZ],b[SZ],vis[SZ];
bool cmp(int a,int b){ return a > b; }
int main()
{
int T;
scanf("%d",&T);
while(T --)
{
memset(vis,0,sizeof(vis));
scanf("%d",&n);
for(int i = 1;i <= n;i ++) scanf("%d",&a[i]);
for(int i = 1;i <= n;i ++) scanf("%d",&b[i]);
sort(a + 1,a + n + 1,cmp);
sort(b + 1,b + n + 1,cmp);
int ans = 0;
for(int i = 1;i <= n;i ++)
{
for(int j = 1;j <= n;j ++)
if(a[i] > b[j] && vis[j] == 0)
{
vis[j] = 1;
ans ++;
break;
}
}
printf("%d\n",ans);
}
return 0;
}
F.三角形
题目描述
小明有一根长度为a的木棒,现在小明想将木棒分为多段(每段木棒长度必须为整数),使得分隔后的木棍中,取出的任意三段都不能构成三角形,小明想知道木棒最多被分成几段?
Solution
构造一个Fibonacci数列即可。
数据过大,要用unsigned long long,%llu
代码
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
//__builtin_popcount(n);
#define IOS ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
#define RI register int
const int MOD = 1e9 + 7;
const double PI = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int SZ = 1e7 + 10;
int n;
ll fib[SZ];
int main()
{
fib[1] = fib[2] = 1;
int T;
scanf("%d",&T);
while(T --)
{
ll a;
cin >> a;
ll ans = 0;
if(a >= fib[1])
ans ++;
if(a < fib[1]) a = 0;
else a = a - fib[1];
if(a >= fib[2])
ans ++;
if(a < fib[2]) a = 0;
else a = a - fib[2];
while(a > 0)
{
fib[ans + 1] = fib[ans] + fib[ans - 1];
ll t = fib[ans + 1];
if(a >= fib[ans + 1]) ans ++;
if(a < t) a = 0;
else a -= t;
}
cout << ans << endl;
}
return 0;
}
H.直线
题目描述
平面上存在n条直线。请问n条直线在平面上最多存在多少交点。
Solution
(n – 1) * n / 2
高精度
代码
import java.math.BigInteger;
import java.util.Scanner;
public class Main {
public static void main(String args[])
{
Scanner cin = new Scanner(System.in);
int T;
T = cin.nextInt();
while(T -- > 0)
{
BigInteger n;
n = cin.nextBigInteger();
n = n.multiply(n.subtract(BigInteger.valueOf(1)));
n = n.divide(BigInteger.valueOf(2));
System.out.println(n);
}
}
}
J.最大值
题目描述
有一个字符串s,对于字符串中一个非前缀子串恰好为字符串的前缀我们称之为ac串。
请问给出一个字符串他的ac串最大长度为多少
Solution
KMP算法中处理prefix_table的过程,答案即为prefix_table中的最大值。
代码
//KMP
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int SZ = 1000000 + 10;
int prefix_table[SZ];
int lenb;
char b[SZ];
void find_prefix_table()
{
int j = 0;
for(int i = 2;i <= lenb;i ++ )
{
while(j && b[i] != b[j+1])
j = prefix_table[j];
if(b[j+1] == b[i])
j ++ ;
prefix_table[i] = j;
}
}
int main()
{
int T;
scanf("%d",&T);
while(T --)
{
memset(prefix_table,0,sizeof(prefix_table));
scanf("%s",b + 1);
lenb = strlen(b + 1);
find_prefix_table();
int ans = 0;
for(int i = 1;i <= lenb;i ++)
ans = max(ans,prefix_table[i]);
printf("%d\n",ans);
}
return 0;
}
2020.6.1