博客

计数排序

计数排序是一种非基于比较的

非稳定线性

排序算法。

基本思想是：用空间换时间，本质上是建立了基于元素的Hash表。

1）假设要排序的数组A原始数据为{2，5，3，0，2，3，0，3}，遍历一遍找到最大值为max=5，min=0





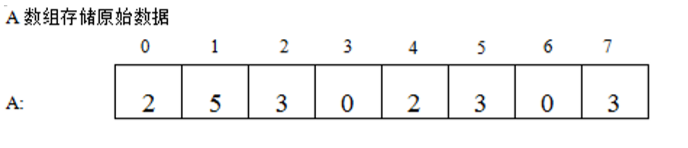
2）定义一个辅助数组C。max-min+1=6，那么C的大小为6，C数组初始化





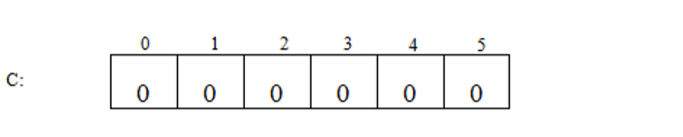
3）C数组用作统计A数组中元素的个数，若A[k]-min==i，则C[i]++，0<=k<7，例如A中的0有2个，那么C[0-min]=2，min=0

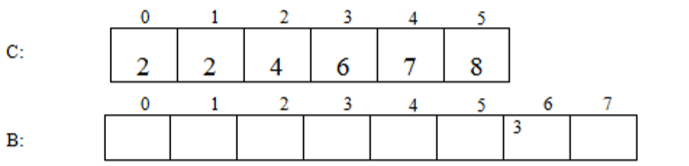
4）C数组用作：统计A数组中，小于等于A[k]的元素的个数，例如小于等于（2+min）的元素有C[0]+C[1]+C[2]=4

声明一个新数组B，大小与数组一样执行循环，从数组A最后一个元素开始，例如i=7，A[7]=3，C[3]=7（C[A[7]]=7），B[7-1]=3，C[3]=7-1=6

1、时间复杂度

时间与空间复杂度均为O(n)

。

基于比较的排序算法时间复杂度最小是O(nlogn)的。

计数排序、桶排序与基数排序都是线性排序。

2、代码实现

void CountSort(vector<int>& a, int size) 
{  
  int max = a[0]; 
  int min = a[0]; 
  for (int i = 0; i < size; ++i) 
  { 
    if (a[i] > max) 
    { 
      max = a[i]; 
    } 
    if (a[i] < min) 
    { 
      min = a[i]; 
    } 
  } 
  int range = max - min + 1; 
  vector<int> count(range ,0);  
  //统计每个数出现的次数 
  for (int i = 0; i < size; ++i)    
  { 
    count[a[i]-min]++; 
  } 
  //写回到原数组 
  int index = 0; 
  for (int i = 0; i < range; ++i)  //从开辟的数组中读取，开辟的数组大小为range 
  { 
    while (count[i]--) 
    { 
      a[index++] = i + min; 
    } 
  } 
} 

3、应用场景

计数排序仅能对较小整数进行排序，且要求排序的数据的规模不能过大。如满足条件，计数排序将会很快。