FFT算法主要有两种,按时间抽选的FFT的算法(DIT-FFT)和按频率抽选的FFT算法(DIF-FFT)。
时间抽取基-2 FFT算法
设
N
=
2
M
N={
{2}^{M}}
N
=
2
M
,有限长序列
x
(
n
)
x\left( n \right)
x
(
n
)
的离散傅里叶变换(DFT)为
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
e
−
j
n
k
2
π
N
,
0
≤
k
≤
N
−
1
X(k)=\sum\limits_{n=0}^{N-1}{x\left( n \right){
{e}^{-jnk\frac{2\pi }{N}}}},0\le k\le N-1
X
(
k
)
=
n
=
0
∑
N
−
1
x
(
n
)
e
−
j
n
k
N
2
π
,
0
≤
k
≤
N
−
1
直接使用DFT,计算一个
X
(
k
)
X\left( k \right)
X
(
k
)
值,需计算:N次复数相乘和
(
N
−
1
)
\left( N-1 \right)
(
N
−
1
)
次复数相加。计算N点
X
(
k
)
X\left( k \right)
X
(
k
)
值,需计算:
N
2
{
{N}^{2}}
N
2
次复数相乘和
N
(
N
−
1
)
N\left( N-1 \right)
N
(
N
−
1
)
次复数相加。可以看出,在DFT计算中,不论是乘法还是加法,运算量均与
N
2
{
{N}^{2}}
N
2
成正比。这给处理器的运算性能带来了极大的挑战。令
W
N
=
e
−
j
2
π
N
{
{W}_{N}}={
{e}^{-j\frac{2\pi }{N}}}
W
N
=
e
−
j
N
2
π
那么
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
W
N
n
k
,
0
≤
k
≤
N
−
1
X(k)=\sum\limits_{n=0}^{N-1}{x\left( n \right)W_{N}^{nk}},0\le k\le N-1
X
(
k
)
=
n
=
0
∑
N
−
1
x
(
n
)
W
N
n
k
,
0
≤
k
≤
N
−
1
将序列
x
(
n
)
x\left( n \right)
x
(
n
)
按下标偶数项和奇数项分解为两组,偶数项为一组,奇数项为一组,得到两个
N
/
2
N/2
N
/
2
点的子序列,即
{
x
1
(
r
)
=
x
(
2
r
)
x
2
(
r
)
=
x
(
2
r
+
1
)
r
=
0
,
1
,
⋯
,
N
/
2
−
1
\left\{ \begin{aligned} & {
{x}_{1}}\left( r \right)=x\left( 2r \right) \\ & {
{x}_{2}}\left( r \right)=x\left( 2r+1 \right) \\ \end{aligned} \right.r=0,1,\cdots ,N/2-1
{
x
1
(
r
)
=
x
(
2
r
)
x
2
(
r
)
=
x
(
2
r
+
1
)
r
=
0
,
1
,
⋯
,
N
/
2
−
1
则
X
(
k
)
=
∑
r
=
0
N
/
2
−
1
x
(
2
r
)
W
N
2
r
k
+
∑
r
=
0
N
/
2
−
1
x
(
2
r
+
1
)
W
N
(
2
r
+
1
)
k
X\left( k \right)=\sum\limits_{r=0}^{N/2-1}{x\left( 2r \right)}W_{N}^{2rk}+\sum\limits_{r=0}^{N/2-1}{x\left( 2r+1 \right)}W_{N}^{(2r+1)k}
X
(
k
)
=
r
=
0
∑
N
/
2
−
1
x
(
2
r
)
W
N
2
r
k
+
r
=
0
∑
N
/
2
−
1
x
(
2
r
+
1
)
W
N
(
2
r
+
1
)
k
又因为
W
N
2
r
k
=
e
−
j
2
π
N
2
r
k
=
e
−
j
2
π
N
/
2
r
k
=
W
N
/
2
r
k
W_{N}^{2rk}={
{e}^{-j\frac{2\pi }{N}2rk}}={
{e}^{-j\frac{2\pi }{N/2}rk}}=W_{N/2}^{rk}
W
N
2
r
k
=
e
−
j
N
2
π
2
r
k
=
e
−
j
N
/
2
2
π
r
k
=
W
N
/
2
r
k
所以
X
(
k
)
=
∑
r
=
0
N
/
2
−
1
x
(
2
r
)
W
N
/
2
r
k
+
∑
r
=
0
N
/
2
−
1
x
(
2
r
+
1
)
W
N
k
W
N
/
2
r
k
X\left( k \right)=\sum\limits_{r=0}^{N/2-1}{x\left( 2r \right)}W_{N/2}^{rk}+\sum\limits_{r=0}^{N/2-1}{x(2r+1)W_{N}^{k}W_{N/2}^{rk}}
X
(
k
)
=
r
=
0
∑
N
/
2
−
1
x
(
2
r
)
W
N
/
2
r
k
+
r
=
0
∑
N
/
2
−
1
x
(
2
r
+
1
)
W
N
k
W
N
/
2
r
k
上式又可以写作
X
(
k
)
=
∑
r
=
0
N
/
2
−
1
x
1
(
r
)
W
N
/
2
r
k
+
W
N
k
∑
r
=
0
N
/
2
−
1
x
2
(
r
)
W
N
/
2
r
k
=
X
1
(
k
)
+
W
N
k
X
2
(
k
)
\begin{aligned} & X\left( k \right)=\sum\limits_{r=0}^{N/2-1}{
{
{x}_{1}}}\left( r \right)W_{N/2}^{rk}+W_{N}^{k}\sum\limits_{r=0}^{N/2-1}{
{
{x}_{2}}}\left( r \right)W_{N/2}^{rk} \\ & \begin{matrix} \begin{matrix} {} & {} \\ \end{matrix} & ={
{X}_{1}} \\ \end{matrix}\left( k \right)+W_{N}^{k}{
{X}_{2}}\left( k \right) \\ \end{aligned}
X
(
k
)
=
r
=
0
∑
N
/
2
−
1
x
1
(
r
)
W
N
/
2
r
k
+
W
N
k
r
=
0
∑
N
/
2
−
1
x
2
(
r
)
W
N
/
2
r
k
=
X
1
(
k
)
+
W
N
k
X
2
(
k
)
同理可得
X
(
k
+
N
2
)
=
X
1
(
k
)
−
W
N
k
X
2
(
k
)
k
=
0
,
1
,
.
.
.
,
N
/
2
−
1
X\left( k+\frac{N}{2} \right)={
{X}_{1}}\left( k \right)-W_{N}^{k}{
{X}_{2}}\left( k \right)\begin{matrix} {} & k=0,1,…,N/2-1 \\ \end{matrix}
X
(
k
+
2
N
)
=
X
1
(
k
)
−
W
N
k
X
2
(
k
)
k
=
0
,
1
,
.
.
.
,
N
/
2
−
1
那么,傅里叶变换可以写作
{
X
(
k
)
=
X
1
(
k
)
+
W
N
k
X
2
(
k
)
X
(
k
+
N
2
)
=
X
1
(
k
)
−
W
N
k
X
2
(
k
)
k
=
0
,
1
,
.
.
.
,
N
/
2
−
1
\left\{ \begin{aligned} & X\left( k \right)={
{X}_{1}}\left( k \right)+W_{N}^{k}{
{X}_{2}}\left( k \right) \\ & X\left( k+\frac{N}{2} \right)={
{X}_{1}}\left( k \right)-W_{N}^{k}{
{X}_{2}}\left( k \right) \\ \end{aligned} \right.\begin{matrix} {} & k=0,1,…,N/2-1 \\ \end{matrix}
⎩
⎪
⎨
⎪
⎧
X
(
k
)
=
X
1
(
k
)
+
W
N
k
X
2
(
k
)
X
(
k
+
2
N
)
=
X
1
(
k
)
−
W
N
k
X
2
(
k
)
k
=
0
,
1
,
.
.
.
,
N
/
2
−
1
通过M次分解最后分解成2点的DFT运算。则,时间抽取基-2 FFT总共需要的运算量为:复乘:
N
/
2
⋅
M
=
N
/
2
⋅
log
2
N
N/2\cdot M=N/2\cdot {
{\log }_{2}}N
N
/
2
⋅
M
=
N
/
2
⋅
lo
g
2
N
,复加:
N
⋅
M
=
N
log
2
N
N\cdot M=N{
{\log }_{2}}N
N
⋅
M
=
N
lo
g
2
N
。显然,要比直接DFT运算快得多。
频率抽取基-2 FFT算法
DIF-FFT算法是将输入序列
X
(
k
)
X\left( k \right)
X
(
k
)
分成前后两个部分
X
(
k
)
=
∑
n
=
=
0
N
−
1
x
(
n
)
W
N
n
k
=
∑
n
=
0
N
2
−
1
x
(
n
)
W
N
n
k
+
∑
n
=
N
2
N
−
1
x
(
n
)
W
N
n
k
=
∑
n
=
0
N
−
1
x
(
n
)
W
N
n
k
+
∑
n
=
0
N
−
1
x
(
n
+
N
2
)
W
N
k
(
n
+
N
2
)
=
∑
n
=
0
N
2
−
1
[
x
(
n
)
+
x
[
n
+
N
2
]
W
N
N
k
/
2
]
W
N
n
k
\begin{aligned} & X\left( k \right)=\sum\limits_{n==0}^{N-1}{x\left( n \right)W_{N}^{nk}}=\sum\limits_{n=0}^{\frac{N}{2}-1}{x\left( n \right)W_{N}^{nk}}+\sum\limits_{n=\frac{N}{2}}^{N-1}{x\left( n \right)W_{N}^{nk}} \\ & =\sum\limits_{n=0}^{N-1}{x\left( n \right)W_{N}^{nk}}+\sum\limits_{n=0}^{N-1}{x\left( n+\frac{N}{2} \right)W_{N}^{k\left( n+\frac{N}{2} \right)}} \\ & =\sum\limits_{n=0}^{\frac{N}{2}-1}{\left[ x\left( n \right)+x\left[ n+\frac{N}{2} \right]W_{N}^{Nk/2} \right]W_{N}^{nk}} \end{aligned}
X
(
k
)
=
n
=
=
0
∑
N
−
1
x
(
n
)
W
N
n
k
=
n
=
0
∑
2
N
−
1
x
(
n
)
W
N
n
k
+
n
=
2
N
∑
N
−
1
x
(
n
)
W
N
n
k
=
n
=
0
∑
N
−
1
x
(
n
)
W
N
n
k
+
n
=
0
∑
N
−
1
x
(
n
+
2
N
)
W
N
k
(
n
+
2
N
)
=
n
=
0
∑
2
N
−
1
[
x
(
n
)
+
x
[
n
+
2
N
]
W
N
N
k
/
2
]
W
N
n
k
因为
W
N
N
/
2
=
−
1
W_{N}^{N/2}=-1
W
N
N
/
2
=
−
1
,则
W
N
N
k
/
2
=
(
−
1
)
k
=
{
1
k
为
偶
数
−
1
k
为
奇
数
W_{N}^{Nk/2}={
{\left( -1 \right)}^{k}}=\left\{ \begin{matrix} 1 & k为偶数 \\ -1 & k为奇数 \\ \end{matrix} \right.
W
N
N
k
/
2
=
(
−
1
)
k
=
{
1
−
1
k
为
偶
数
k
为
奇
数
,所以可以得到
X
(
k
)
=
∑
n
=
0
N
2
−
1
[
x
(
n
)
+
(
−
1
)
k
x
(
n
+
N
2
)
]
W
N
n
k
X(k)=\sum\limits_{n=0}^{\frac{N}{2}-1}{\left[ x\left( n \right)+{
{\left( -1 \right)}^{k}}x\left( n+\frac{N}{2} \right) \right]W_{N}^{nk}}
X
(
k
)
=
n
=
0
∑
2
N
−
1
[
x
(
n
)
+
(
−
1
)
k
x
(
n
+
2
N
)
]
W
N
n
k
将k按照奇数和偶数来分,得到
{
k
=
2
r
k
为
偶
数
k
=
2
r
+
1
k
为
奇
数
r
=0,1,
⋯
N/2-1
\left\{ \begin{matrix} k=2r & k为偶数 \\ k=2r+1 & k为奇数 \\ \end{matrix} \right.r\text{=0,1,}\cdots \text{N/2-1}
{
k
=
2
r
k
=
2
r
+
1
k
为
偶
数
k
为
奇
数
r
=0,1,
⋯
N/2-1
将X(k)分为两部分
{
X
(
2
r
+
1
)
=
∑
n
=
0
N
2
−
1
[
x
(
n
)
−
x
(
n
+
N
2
)
]
W
N
n
W
N
/
2
r
n
X
(
2
r
)
=
∑
n
=
0
N
2
−
1
[
x
(
n
)
+
x
(
n
+
N
2
)
]
W
N
/
2
r
n
\left\{ \begin{aligned} & X\left( 2r+1 \right)=\sum\limits_{n=0}^{\frac{N}{2}-1}{\left[ x\left( n \right)-x\left( n+\frac{N}{2} \right) \right]W_{N}^{n}W_{N/2}^{rn}} \\ & X\left( 2r \right)=\sum\limits_{n=0}^{\frac{N}{2}-1}{\left[ x\left( n \right)+x\left( n+\frac{N}{2} \right) \right]W_{N/2}^{rn}} \\ \end{aligned} \right.
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎧
X
(
2
r
+
1
)
=
n
=
0
∑
2
N
−
1
[
x
(
n
)
−
x
(
n
+
2
N
)
]
W
N
n
W
N
/
2
r
n
X
(
2
r
)
=
n
=
0
∑
2
N
−
1
[
x
(
n
)
+
x
(
n
+
2
N
)
]
W
N
/
2
r
n
令
x
1
=
x
(
n
)
+
x
(
n
+
N
2
)
{
{x}_{1}}=x\left( n \right)+x\left( n+\frac{N}{2} \right)
x
1
=
x
(
n
)
+
x
(
n
+
2
N
)
,
x
2
(
n
)
=
[
x
(
n
)
−
x
(
n
+
N
2
)
]
W
N
n
{
{x}_{2}}\left( n \right)=\left[ x\left( n \right)-x\left( n+\frac{N}{2} \right) \right]W_{N}^{n}
x
2
(
n
)
=
[
x
(
n
)
−
x
(
n
+
2
N
)
]
W
N
n
,可以得到
{
X
(
2
r
+
1
)
=
∑
n
=
0
N
2
−
1
x
2
(
n
)
W
N
/
2
r
n
X
(
2
r
)
=
∑
n
=
0
N
2
−
1
x
1
(
n
)
W
N
/
2
r
n
\left\{ \begin{aligned} & X\left( 2r+1 \right)=\sum\limits_{n=0}^{\frac{N}{2}-1}{
{
{x}_{2}}\left( n \right)W_{N/2}^{rn}} \\ & X\left( 2r \right)=\sum\limits_{n=0}^{\frac{N}{2}-1}{
{
{x}_{1}}\left( n \right)W_{N/2}^{rn}} \\ \end{aligned} \right.
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎧
X
(
2
r
+
1
)
=
n
=
0
∑
2
N
−
1
x
2
(
n
)
W
N
/
2
r
n
X
(
2
r
)
=
n
=
0
∑
2
N
−
1
x
1
(
n
)
W
N
/
2
r
n
则经过M次分解,同样可以将DFT分解成为N/2个两点DFT。以8点DIF-FFT运算为例,DIF-FFT运算流图如下图所示
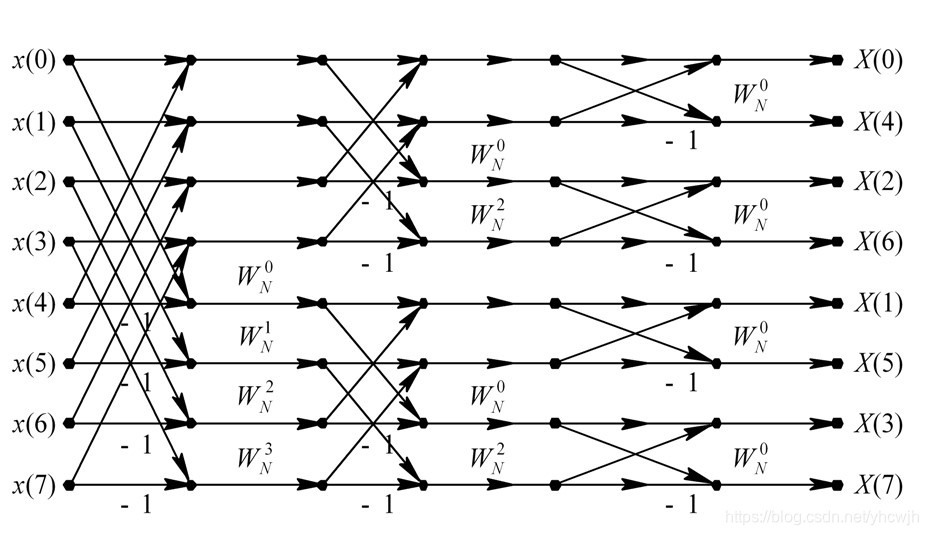
从上图可以看出,输出序列的排列规律不是从小到大按顺序的,而是按照倒叙规则排序的,即先将0-7转换为二进制数,然后将二进制数左右倒序,再转为十进制就可以得到新的数列,即:0,4,2,6,1,5,3,7。
利用MATLAB实现DFT
DFT的矩阵表示形式为
[
X
(
0
)
X
(
1
)
X
(
2
)
⋯
X
(
N
−
1
)
]
=
[
W
N
0
W
N
0
W
N
0
⋯
W
N
0
W
N
0
W
N
1
W
N
2
⋯
W
N
N
−
1
W
N
0
W
N
2
W
N
4
⋯
W
N
2
(
N
−
1
)
⋯
W
N
0
⋯
W
N
N
−
1
⋯
W
N
2
(
N
−
1
)
⋯
⋯
⋯
W
N
(
N
−
1
)
(
N
−
1
)
]
[
x
(
0
)
x
(
1
)
x
(
2
)
⋯
x
(
N
−
1
)
]
\left[ \begin{matrix} X\left( 0 \right) \\ X\left( 1 \right) \\ X\left( 2 \right) \\ \begin{matrix} \cdots \\ X\left( N-1 \right) \\ \end{matrix} \\ \end{matrix} \right]=\left[ \begin{matrix} W_{N}^{0} & W_{N}^{0} & W_{N}^{0} & \begin{matrix} \cdots & W_{N}^{0} \\ \end{matrix} \\ W_{N}^{0} & W_{N}^{1} & W_{N}^{2} & \begin{matrix} \cdots & W_{N}^{N-1} \\ \end{matrix} \\ W_{N}^{0} & W_{N}^{2} & W_{N}^{4} & \begin{matrix} \cdots & W_{N}^{2\left( N-1 \right)} \\ \end{matrix} \\ \begin{matrix} \cdots \\ W_{N}^{0} \\ \end{matrix} & \begin{matrix} \cdots \\ W_{N}^{N-1} \\ \end{matrix} & \begin{matrix} \cdots \\ W_{N}^{2\left( N-1 \right)} \\ \end{matrix} & \begin{matrix} \begin{matrix} \cdots & \cdots \\ \end{matrix} \\ \begin{matrix} \cdots & W_{N}^{\left( N-1 \right)\left( N-1 \right)} \\ \end{matrix} \\ \end{matrix} \\ \end{matrix} \right]\left[ \begin{matrix} x\left( 0 \right) \\ x\left( 1 \right) \\ x\left( 2 \right) \\ \begin{matrix} \cdots \\ x\left( N-1 \right) \\ \end{matrix} \\ \end{matrix} \right]
⎣
⎢
⎢
⎢
⎢
⎡
X
(
0
)
X
(
1
)
X
(
2
)
⋯
X
(
N
−
1
)
⎦
⎥
⎥
⎥
⎥
⎤
=
⎣
⎢
⎢
⎢
⎢
⎡
W
N
0
W
N
0
W
N
0
⋯
W
N
0
W
N
0
W
N
1
W
N
2
⋯
W
N
N
−
1
W
N
0
W
N
2
W
N
4
⋯
W
N
2
(
N
−
1
)
⋯
W
N
0
⋯
W
N
N
−
1
⋯
W
N
2
(
N
−
1
)
⋯
⋯
⋯
W
N
(
N
−
1
)
(
N
−
1
)
⎦
⎥
⎥
⎥
⎥
⎤
⎣
⎢
⎢
⎢
⎢
⎡
x
(
0
)
x
(
1
)
x
(
2
)
⋯
x
(
N
−
1
)
⎦
⎥
⎥
⎥
⎥
⎤
根据DFT公式和矩阵展开形式,利用MATLAB可以得到如下结果
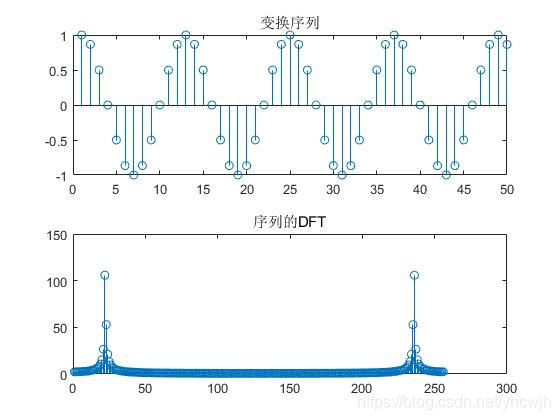
利用MATLAB实现FFT(8点DIF-FFT为例)
由DIF-FFT的流程图可以得到,FFT运算的基本单元是蝶形运算单元。蝶形运算单元可以用简单的语句实现,然后可以用循环语句来进行各个蝶形运算单元的运算。
8点FFT的蝶形运算有3级,第1级有1组,每组4个蝶形运算单元,旋转因子是
W
8
0
W_{8}^{0}
W
8
0
、
W
8
1
W_{8}^{1}
W
8
1
、
W
8
2
W_{8}^{2}
W
8
2
、
W
8
3
W_{8}^{3}
W
8
3
;第2级有2组,每组2个蝶形运算单元,循环因子是
W
4
0
W_{4}^{0}
W
4
0
,
W
4
1
W_{4}^{1}
W
4
1
;第3级有4组,每组1个蝶形运算单元,旋转因子是
W
2
0
W_{2}^{0}
W
2
0
。总结运算规律,来设定循环语句。
第一层循环在1到3级间循环,循环变量
m
m
=
1
,
2
,
3
mm=1,2,3
m
m
=
1
,
2
,
3
。旋转因子下标
N
m
=
2
4
−
m
m
=
8
,
4
,
2
N_{m}=2^{4-mm}=8,4,2
N
m
=
2
4
−
m
m
=
8
,
4
,
2
。
第二层循环在该级的各组间循环,每级有
2
m
m
−
1
2^{mm-1}
2
m
m
−
1
组,每组第一行对应的
x
x
x
值为:第1级是
x
(
0
)
x(0)
x
(
0
)
,第2级是
x
(
0
)
x(0)
x
(
0
)
,
x
(
4
)
x(4)
x
(
4
)
,第3级是
x
(
0
)
x(0)
x
(
0
)
,
x
(
2
)
x(2)
x
(
2
)
,
x
(
4
)
x(4)
x
(
4
)
,
x
(
6
)
x(6)
x
(
6
)
。设第二层循环变量为
p
p
p
,则在MATLAB中,
p
=
0
:
N
m
:
7
p=0:N_{m}:7
p
=
0
:
N
m
:
7
。
第三层循环在该组的各个蝶形运算单元间循环,每组有
N
m
2
\frac{
{
{N}_{m}}}{2}
2
N
m
个蝶形运算单元,则循环变量
k
k
k
从1到
N
m
2
\frac{
{
{N}_{m}}}{2}
2
N
m
,旋转因子是
e
−
2
π
(
k
−
1
)
j
N
m
{
{e}^{\frac{-2\pi (k-1)j}{Nm}}}
e
N
m
−
2
π
(
k
−
1
)
j
,每次蝶形运算跨越的行数是
N
m
2
\frac{
{
{N}_{m}}}{2}
2
N
m
,则参加蝶形运算的
x
x
x
值为
x
(
k
+
p
)
x(k+p)
x
(
k
+
p
)
和
x
(
k
+
p
+
N
m
2
)
x(k+p+\frac{
{
{N}_{m}}}{2})
x
(
k
+
p
+
2
N
m
)
。
循环完成后则FFT运算完成,再将x序列按倒叙规律重新排列就可以得到
X
(
k
)
X(k)
X
(
k
)
序列。
涉及到的MATLAB函数
exp(x)计算e的x次方,abs(x)计算x绝对值。
倒序运算主要用到的函数有,dec2bin(x,m),是把十进制序列x转换为m位二进制数,bin2dec(x,m)也是类似功能。
fliplr函数是将一个矩阵左右颠倒,则程序中求倒序的语句就是:d=bin2dec(fliplr(dec2bin([0:N-1],m)))+1;y=x(d); 其中,x是N点序列,执行完语句后,y序列就是x序列的倒序排列。
根据上述流程,可以得到结果如下
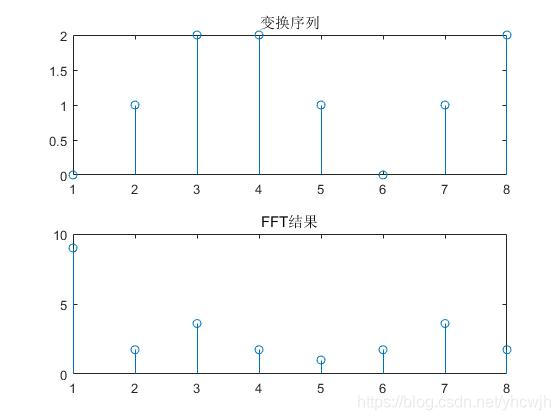
调用MATLAB的FFT函数
MATLAB自带的FFT函数语法格式为:A=fft(X,N)。A返回信号X的FFT变换矩阵,输入信号X和输出信号A大小相同。N为FFT的点数,当X长度不足N,自动在数据末尾补零,当X长度超过N,则进行自动截取。结果如下
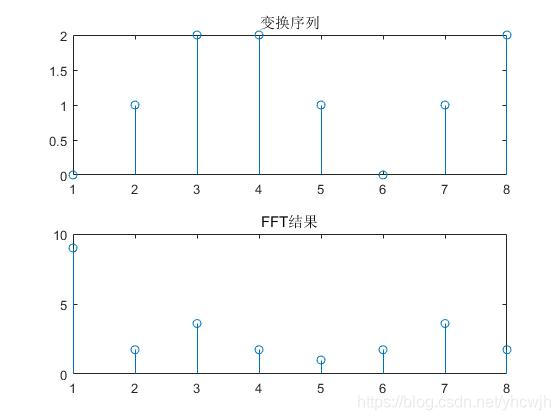
通过对比可以发现,和上述实现的FFT结果是一致的。
实验一代码如下:
clear;
close all;
clc;
N=256; %信号点数
n=0:N-1; %时间采样
xn=cos(pi*n/6); %信号
k=0:N-1; %频域采样
WN=exp(-1j*2*pi/N);
nk=n'*k;
WNnk=WN.^nk;
Xk=xn*WNnk; %计算DFT
figure(1);
subplot(2,1,1);stem(xn);title('变换序列');xlim([0 50])
subplot(2,1,2);stem(abs(Xk));title('序列的DFT');
实验二代码如下:
clear;
close all;
clc;
N=8; %FFT点数
n=0:N-1;
x=[0 1 2 2 1 0 1 2]; %变换序列
figure(1);
subplot(2,1,1);stem(x);title('变换序列');
x1=x;
m=log2(N); %蝶形运算的级数
for mm=1:m %循环蝶形运算
Nm=2^(m-mm+1); %旋转因子下标Nm=8, 4, 2
for p=0:Nm:N-1 %循环该级1~2mm-1组蝶形运算
for k=1:Nm/2
kp=k+Nm/2+p; %蝶形运算的下标
a=x(kp);
x(kp)=(x(k+p)-a)*exp(-1j*2*pi*(k-1)/Nm);
x(k+p)=x(k+p)+a;
end
end
end
d=bin2dec(fliplr(dec2bin([0:N-1],m)))+1; %倒序排列
y=x(d);
mag=abs(y);
subplot(2,1,2);stem(mag);title('FFT结果');
x=[0 1 2 2 1 0 1 2];
yy=fft(x,N);
figure(2);
subplot(2,1,1);stem(x);title('变换序列');
subplot(2,1,2);stem(abs(yy));title('FFT结果');