目录
一、 梯度下降
在机器学习中,最简单就是没有任何优化的梯度下降(GD,Gradient Descent),我们每一次循环都是
对整个训练集进行学习
,这叫做批量梯度下降(Batch Gradient Descent),我们之前说过了最核心的参数更新的公式,这里我们再来看一下:
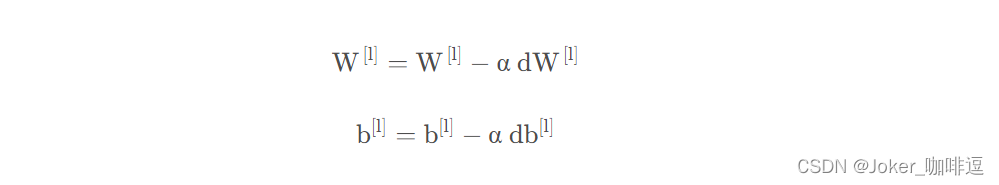
- l :当前的层数
- α :学习率
特点
: 准确性高,但速度慢
二、 随机梯度下降
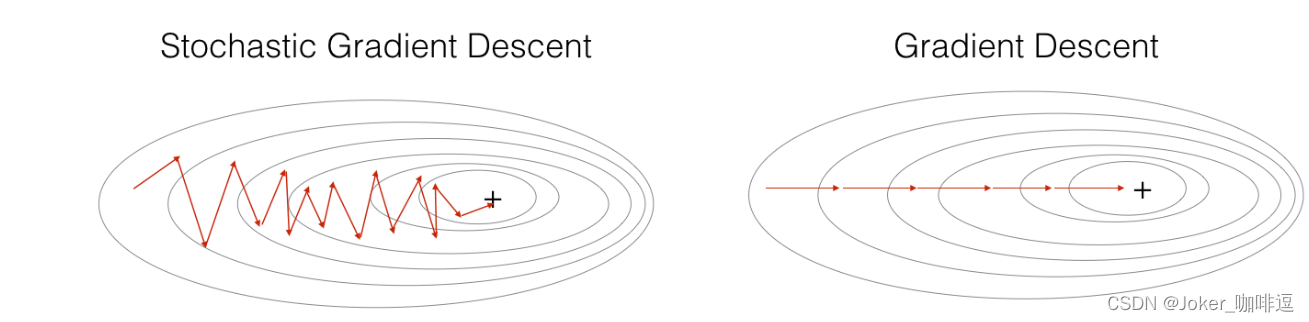
在随机梯度下降中,在更新梯度之前,只使用1个训练样本。 当训练集较大时,随机梯度下降可以更快,但是参数会向最小值摆动,而不是平稳地收敛,我们来看一下比较图:
特点
: 每次只用一个样本,迭代速度快,但每次不一定朝收敛方向
三、 小批量梯度下降法(mini-batch)
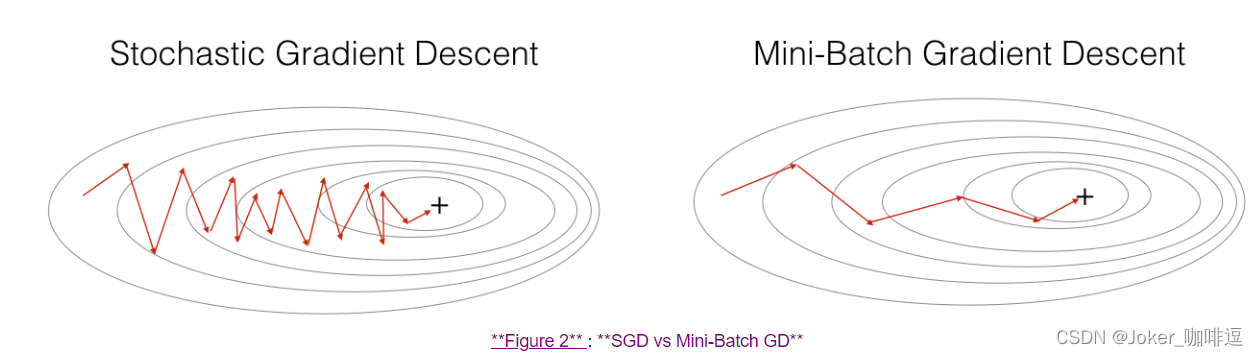
在实际中,更好的方法是使用小批量(mini-batch)梯度下降法。小批量梯度下降法是一种综合了梯度下降法和随机梯度下降法的方法,在它的每次迭代中,既不是选择全部的数据来学习,也不是选择一个样本来学习,而是把所有的数据集分割为一小块一小块的来学习,它会随机选择一小块(mini-batch),块大小一般为2的n次方倍。一方面,充分利用的GPU的并行性,更一方面,不会让计算时间特别长,来看一下比较图:
我们要使用mini-batch要经过两个步骤:
-
-
把训练集打乱,但是X和Y依旧是一一对应的
。X的第i列是与Y中的第i个标签对应的样本。乱序步骤确保将样本被随机分成不同的小批次。
-
如果你不好理解的话请看一下下面的伪代码,看看X和Y是如何根据permutation来打乱顺序的。
x = np.array([[1,2,3,4,5,6,7,8,9],
[9,8,7,6,5,4,3,2,1]])
y = np.array([[1,0,1,0,1,0,1,0,1]])
random_mini_batches(x,y)
permutation= [7, 2, 1, 4, 8, 6, 3, 0, 5]
shuffled_X= [[8 3 2 5 9 7 4 1 6]
[2 7 8 5 1 3 6 9 4]]
shuffled_Y= [[0 1 0 1 1 1 0 1 0]]
-
-
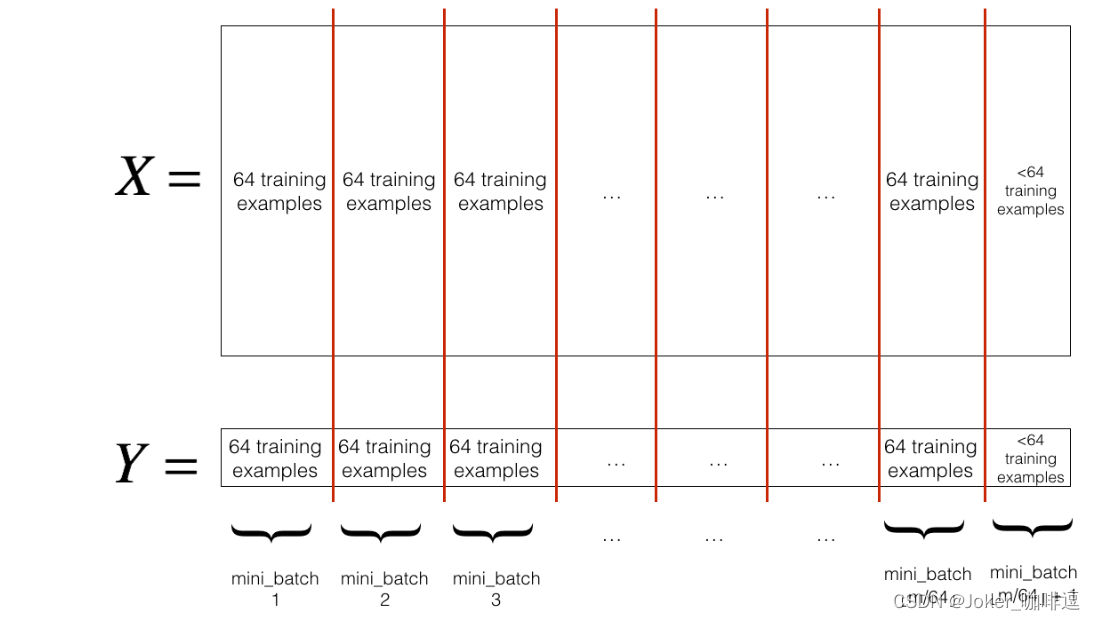
切分
.这里切分的大小是64,如下图:
-
四、包含动量的梯度下降(Momentum)
由于小批量梯度下降只看到了一个子集的参数更新,会造成局部震荡问题,导致趋于局部最优值得速度过慢。
使用动量可以减少这些振荡,动量考虑了过去的梯度以平滑更新, 我们将把以前梯度的方向存储在变量v中,从形式上讲,这将是前面的梯度的指数加权平均值。我们也可以把V看作是滚下坡的速度,根据山坡的坡度建立动量。我们来看一下下面的图:
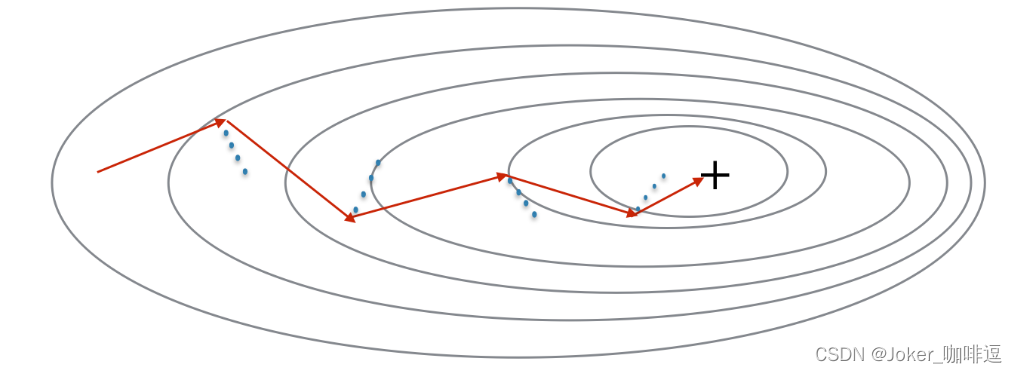
- 红色箭头:具有动量的小批量梯度 下降一步时所采取的方向
- 蓝色的点:每个步骤的梯度方向(相对于当前的小批量)
当然我们不仅要观察梯度,还要让
v
v
v
影响梯度,然后朝
v
v
v
方向前进一步,尽量让前进的方向指向最小值
影响梯度的方向公式:
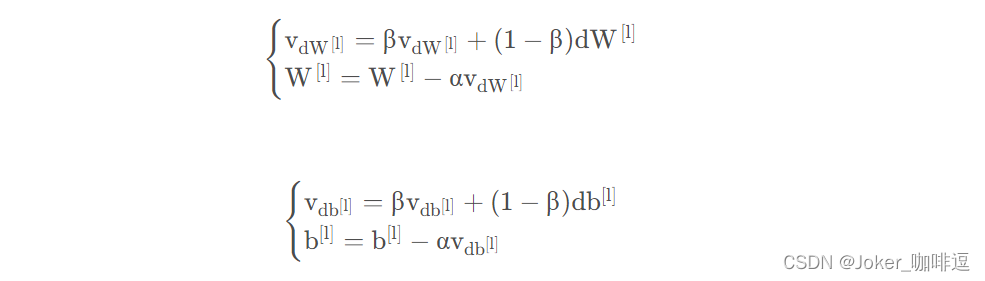
- l :当前神经网络的层数
- β:动量,是一个实数
- α :学习率.

效果:
增加通过
鞍点、局部最小点
的可能性(在局部最小、鞍点处梯度为0)
五、自适应梯度(AdaGrad)与 RMSProp
自适应梯度法:通过减小震荡方向步长,增大平坦方向步长来减少震荡,从而加速通往谷底
什么是梯度方向?什么是平坦方向?
震荡方向: 梯度幅度平方较大的

此方法存在一个问题:
由上图 3,4公式,我们会发现,累加平方梯度会随迭代次数的增大会变得很大,导致权值更新不动
为解决此问题,提出来RMSProp方法
在自适应梯度方法基础上添加了一个
ρ
,
ρ
∈ [0, 1) , 一般设置为0.999

六、 Adam算法
Adam算法是训练神经网络中最有效的算法之一,它是
RMSProp算法
与
Momentum算法
的结合体。
不但使用动量作为参数更新的方向,而且可自适应调整学习率
。
Adam算法(如下图所示)在上述俩算法基础上只是多了一步
修正偏差
:极大的减缓算法初期的冷启动问题
举个例子:
取μ=0.9, ρ = 0.999
则累计梯度 v = 0 + 0.1g 累计平方梯度:r = 0 + 0.001g^2
可以发现 v 和 r 值都很小,则更新速度就很慢
而 添加了
修正偏差
这步骤之后,可以在初期对算法的两个值起到修正作用。当到后面时,通过公式发现,1 – 0.9^t, 当t 不断增大时,该项不断趋于1,则 v 就基本上不更新了,这个步骤就不起作用了。

总的来说,一般初始的时候我们会用
Adam方法
自动去调,当调不动的时候,我们再用
SGD方法
去手动调。