时间复杂度
- 对于算法时间复杂度的分析需要牢记一句话:将算法中基本操作的执行次数作为算法时间复杂度的度量。时间复杂度并不是执行完一段程序的总时间,而是其中基本操作的总次数。
-
在考试的算法题目中你总能找到一个n,称为问题的规模。如你要处理的数组元素的个数为n,而基本操作所执行的次数是n的一个函数f(n)。对于求其基本操作执行的次数,就是求f(n)。求出以后就可以取出f(n)中随n增大而增大的最快的项,将其系数变为1,作为时间复杂度的度量。

计算时间复杂度的步骤
- 确定算法中的基本操作以及问题的规模
-
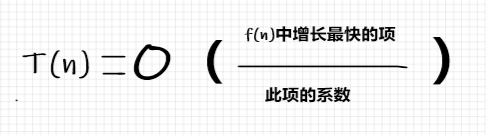
根据基本操作执行情况计算出规模n的函数f(n),并确定时间复杂度T(n)=O(f(n)中增长最快的项/此项的系数)
-
注意:一般将最坏的情况作为算法时间复杂度的度量
例子1:
void fun(int n)
{
int i = 1, j =100;
while(i<n)
{
++j;
i+=2;
}
}
解析:
1.找出基本操作。
显然++j;i+=2;都是基本操作
2.确定规模
确定n之后,可以看出循环是否结束和i有关,设循环m次后结束循环,此时i>n我们可得i最后的值为1+2m我们设1+2m+K=n(因为1+2m>n,所以加
一个常数K来使他们想等从而求得m与n的关系,K是常数并不影响最终时间复杂度)得m=(n-1-K)/2,即f(n)=(n-1-K)/2,其中增长最快的就是
n/2,所以时间复杂度T(n)=O(n).
例子2:
void fun(int n)
{
int i,j,x=0;
for(i=0;i<n;++i)
{
for(j=i+1;j<n;++j)
{
++x;
}
}
}
解析:
1.找出基本操作
++x:处于最内层的循环,所以取++x;为基本操作。
2.确定规模
显然n为规模。
下面列举i,j不同值情况下++x的执行次数
i j ++x
0 1 n-1
1 2 n-2
...........
n-1 n 0
利用等差数列求和的公式求出基本操作的执行次数:n(n-1)/2
变化最快的项为n^2/2,因此时间复杂度为T(n) = O(n^2)
例子3:
void funn(int n)
{
int i=0,s=0;
while(s<n)
{
++i;
s+=i;
}
}
1.找出基本操作
++i和s+=i;都为基本操作
2.确定规模
显然n为规模
设执行m次循环后结束,s1=1, s2=1+2, s3=1+2+3, ..., sm=m(m+1)/2(等差数列求和公式)
求得m与n的关系,然后找出最高项将其系数变为1,得到T(n)=O(根号n)
空间复杂度
一个程序的空间复杂度是指运行完一个程序所需内存的大小。利用程序的空间复杂度,可以对程序的运行所需要的内存多少有个预先估计。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。程序执行时所需存储空间包括以下两部分。
(1)固定部分。这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间(即代码空间)、数据空间(常量、简单变量)等所占的空间。这部分属于静态空间。
(2)可变空间,这部分空间的主要包括动态分配的空间,以及递归栈所需的空间等。这部分的空间大小与算法有关。
一个算法所需的存储空间用f(n)表示。S(n)=O(f(n)) 其中n为问题的规模,S(n)表示空间复杂度。
- 设计算法时,时间复杂度要比空间复杂度更容易出问题,所以一般情况一下我们只对时间复杂度进行研究。一般面试或者工作的时候没有特别说明的话,复杂度就是指时间复杂度。
版权声明:本文为qq1350975694原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。