博客

离散数学 第十章 图的基本概念

  • Post author:
  • Post category:其他



目录


10.1 图的基本概念


10.2 道路与回路


10.3 图的连通性


10.4 图的矩阵表示

10.1 图的基本概念

①什么是图：一个序偶(V,E)，记作G=(V,E)


V(G)={v1,v2,…,vn} 结点集，n为G的阶


E(G)={e1,e2,…,em} 边集，m为G的边数

②图的分类：

1.无向图（无向边，e=(u,v)）

2.有向图（有向边，e=(u,v)），e是u的出边，e是v的入边

3.混合图（无向边+有向边）

4.多重图：含有平行边

5.广义图（伪图）：含环的多重图

6.简单图（基图）

③

结点的度数

：
deg(v)=deg^{+}(v)+deg^{-}(v)
出度+入度

最大点度：△，最小点度：
\delta

④

握手定理

：对于任何(n,m)图G=(V,E)，所有结点的度数总和等于边的两倍。

\sum_{v\in V}^{}deg(v)=2m

⑤二部图：设图G=(V,E),若它的结点集可划分为X,Y两个子集，使得它的每一条边的一个关联结点在X中，另一个关联结点在Y中

完全二部图：设|X|=n1,|Y|=n2,X中的每一个结点与Y中的全部结点都邻接，记为Kn1,n2

⑥完全图：

1.无向完全图：G中任一结点都与其余n-1个结点相邻接，Kn

边数

：
\frac{n\times (n-1)}{2}

2.有向完全图：
\forall u,v\in V(u\neq v)
,既有<u,v>，又有<v,u>，Kn

边数

：n(n-1)

⑦补图：设G=<V,E>为具有n个结点的简单图，从完全图Kn中删去G中的所有边而得到的图称为G相对于完全图Kn的补图，记为
\bar{G}

⑧图的同构：设两个图G=<V,E>和
G^{'}=<V^{'},E^{'}>
，若存在双射函数
g:v\rightarrow v^{'}
，使得
\forall e=(vi,vj)\in E
当且仅当
e^{'}=(g(vi),g(vj))\in E^{'}
，则称G与
G^{'}
同构，记为
G\cong G^{'}
。


几个概念：

1.零图：仅由孤立结点组成的图

2.平凡图：仅含一个结点的零图

3.(n,m)图：含有n个结点，m条边的图

4.正则图：各点度数相等的图

5.k度正则图：各点度数为k的图


几个推论：

1.在图G=<V,E>中，其V={v1,v2,…,vn}，E={e1,e2,…,em}，度数为奇数的结点个数为偶数。

2.子图（G=<V1,,E1>  H=<V2,E2>）


子图

真子图

生成子图：V2=V1

平凡子图：V2=V1且E2=E1或
E2\neq \o

删点子图：删除结点及其关联的全部边，G-V

删边子图：从G中删去边e后得到的图，G-e

点诱导子图：G(s)=(S,E’),
S\subseteq
原图结点，
E^{'}\subseteq E
（原图中两结点有的所有边）

边诱导子图：G(T)是一个以T为边集，
T\subseteq E
且
T\neq \o

3.同构

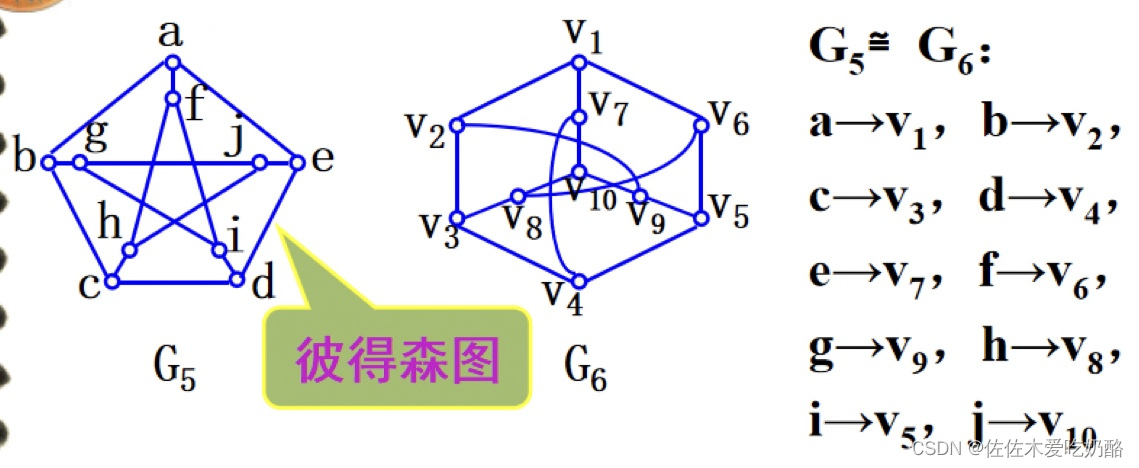
10.2 道路与回路

定义：图G=<V,E>中结点和边相继交错出现的序列P=v0e1v1e2v2…ekvk，则称P为结点v0到结点vk的道路，记<v0,vk>


※简单道路&回路

简单道路：道路中所有边互不相同

回路：闭的简单道路


※基本道路&基本回路（圈）

基本道路：道路中所有结点互不相同

基本回路：除头尾结点其余互不相同

！基本道路（回路）一定是简单道路（回路）


※道路图&圈图

道路图：一个图能以一条基本道路表示出来，记Pn

圈图：一个图能以一个圈表示出来，记Cn

10.3 图的连通性

1.无向图的连通性：结点u,v是连通的，记为u~v。对任意结点u，规定u~u

2.

点诱导子图G（Vi）是G的极大连通子图，称为G的支

。

图G的分支数记为w(G)


※连通图

若无向图G=<V,E>中任意两个结点都是连通的，w(G)=1


※距离

在图G=<V,E>中，从vi到vj存在长度最短的道路，记为d(vi,vj)


注：当vi到vj不存在道路时，d(vi,vj)=
\infty


※点割集（割集）

设无向图G=<V,E>。若存在结点子集
v'\subset v
，使得删除V’后，所得子图G-V’的连通分支数满足w(G-V’)>w(G)，则称v’为G的一个点割集。

若点割集中只有一个结点v,则称v为割点。

割点：对于连通图中的一个点，如果去掉这个点后，原来的图变成非连通图。

点割集：对与连通的一个点集合A，如果去掉A中所有点后，原来的图变成非连通图。


※边割集

设无向图G=<V,E>。若存在边集子集
E'\subset E
，使得删除E’后，所得子图G-E’的连通分支数与G的连通分支数满足w(G-E’)>w(G)

若割集中只有一条边e，则称e为割边


※点连通度&边连通度

点连通度：
\kappa (G)=min
{|v’|  | v’为G的点割集}

边连通度：
\lambda (G)=min
{|E’|  |E’为G的边割集}

\kappa
越大，连通性越好

定理：对任意无向图G=<V,E>：
\kappa (G)\leq \lambda (G)\leq \delta (G)
（点连通度≤边连通度≤结点的最小度数）

3.有向图的连通性：若存在从结点u到结点v的道路，则称从u到v是可达的，记u—>v。对任意结点u，u—>u。


※强连通图、单向连通图（设有向图G=<V,E>是连通图）

强连通图：任意两结点互相可达

单向连通图：任意两结点至少一方可达


※弱连通图（若G的基图是连通的）

一个有向图的基图是去掉边的方向后得到的无向图

定理：一个有向图G是强连通图当且仅当G中有一条包含每一个结点的有向闭道路


※弱分图&单向分图&强分图



10.4 图的矩阵表示

①邻接矩阵——>研究图的道路问题

②道路矩阵（可达性矩阵）

③关联矩阵——>研究子图的问题——>入度与出度


※有向图的邻接矩阵与道路的关系


※可达性矩阵

如果将邻接矩阵看成关系矩阵A，则求可达性矩阵就相当于求A的传递闭包。因此可采样


Warshall算法来求可达性矩阵


。


※构造有向图的全部强分图的方法


※关联矩阵




版权声明：本文为xiaoxiao20020505原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。