机器学习之朴素贝叶斯分类器附C++代码

一、基本概念：

先验概率

(prior probability)：是指根据以往经验和分析得到的概率，如全概率公式，它往往作为”由因求果”问题中的”因”出现的概率。比如，抛一枚硬币，正面朝上的概率P(A)=1/2,就是先验概率。
联合概率

：表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者P(A,B),或者P（A∩B）。
条件概率

：已知事件A发生的条件下事件B发生概率，条件概率表示为P(B|A)

。

$P(B|A)=\frac{P(AB)}{P(A)}$

后验概率

：例如事件B

₁

、B

₂

、B

₃

等都会导致事件A发生。现在事件A已经发生，求事件A发生是由B

₁

、B

₂

、B

₃

那个事件引起的条件概率P(B

_i

|A),就是后验概率。举个在《概率论》中经常用到的例子，

事件B

₁

、B

₂

、B

₃
代表三个不同的工厂生产零件，

事件A是生产次品的事件，

P(A

|B

i

)是

三个工厂的次品率。现在

事件A发生了，判断是由那个工厂生产的这个次品

P(B

_i

|A)

。

二、贝叶斯定理：

在现实生活中,我们可以很容易直接得出P(A|B
_i
)，而P(B
_i
|A)则很难直接得出，但我们更关心P(B
_i
|A)，贝叶斯定理实现了由P(A|B
_i
)计算P(B
_i
|A)的方法。

贝叶斯公式：

$P(B_{i}|A)=\frac{P(B_{i}A)}{P(A)}=\frac{P(A|B_{i})P(B_{i})}{P(A)}$

贝叶斯算法的基础是概率推理，是在各种条件的存在不确定、仅知其出现的概率情况下，完成推理和决策任务。而朴素贝叶斯模型

(Naive Bayesian Model)

是基于独立假设的，即假设样本的每一个特征与其他特征都不相关。

三、贝叶斯分类器基本原理

此时贝叶斯公式写为：

$P(C_{i}|X)=\frac{P(C_{i}X)}{P(X)}=\frac{P(X|C_{i})P(C_{i})}{P(X)}$

训练：

1. 设样本集

$x=\left \{ X_{1},X_{2},X_{3},...X_{n} \right \}$

，其中

$X_{i}=\left \{ a_{1}, a_{2},a_{3},...a_{k}\right \}$

。所有类别集合

$Y=\left \{ C_{1},C_{2},C_{3},...C_{m} \right \}$

。

2. 计算先验概率P(C
_i
)。

3. 计算类条件密度：

$P(a_{1}|C_{1}),P(a_{2}|C_{1}),...P(a_{k}|C_{2});P(a_{1}|C_{2}),P(a_{2}|C_{2}),...P(a_{k}|C_{2});....P(a_{1}|C_{m}),P(a_{2}|C_{m}),...P(a_{k}|C_{m});$

测试：

1.设

$X=\left \{ a_{1},a_{2},a_{3},...a_{k} \right \}$

为待分类项，而每个a
_i
为X的一个特征属性

2.计算

$P(X|C_{i})P(C_{i})=P(a_{1}|C_{i})P(a_{2}|C_{i})...P(a_{k}|C_{i})P(C_{i})=P(C_{i})\prod_{j=1}^{m}P(a_{j}|C_{i})$

3.根据贝叶斯定理求后验概率P(C

_i

|X)，得到X属于C

_i

类别的后验概率；根据最大后验概率判断所属类别。

P(C

_α

|X)=max{P(C
_i
|X)}

$C_{\alpha }\in Y$

，则测试样本属于

C

_α

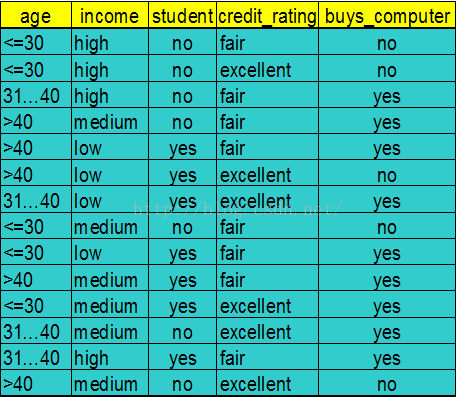
四、举例说明

如图所示，为某电脑卖家统计的客户信息，有14个样本(

X

_1,

X

_{2,

…}

X

₁₄

)，其中

每个样本

有四个属性，

{a

1

(age),a

2

(income),a

3

(student),a

4

(credit_rating)}。根据以上信息，如果再给出一个客户的这四种信息，如{(<30),medium,no,fair},判断他会不会买电脑。也是一个简单的二分类问题。

为了便于表示，把年龄<=30、31—40、>40用Tw(Twenty)、Th(Thirty)、F(Forty)来表示。

训练：

1. 设样本集

$x=\left \{ X_{1},X_{2},X_{3},...X_{14} \right \}$

，其中

$X_{i}=\left \{ a_{1}(age),a_{2}(income),a_{3}(student),a_{4}(credit_rating) \right \}$

。所有类别集合

$Y=\left \{ C_{1}(no), C_{2}(yes)\right \}$

。

2. 计算先验概率P(C

1

)=5/14；P(C

2

)=9/14。

3. 计算类条件密度：

属性a1：P(TwC

1

)=3/14；P(ThC1)=0/14；P(FC1)=2/14；P(TwC2)=2/14；P(ThC2)=4/14；P(FC2)=3/14；

P(Tw

|

C1)=3/5；P(Th|C1)=0/5；P(F|C1)=2/5；P(Tw

|

C2)=2/9；P(Th|C2)=4/9；P(F|C2)=3/9；

属性a2：P(HC

1

)=2/14；P(MC1)=2/14；P(LC1)=1/14；P(HC2)=2/14；P(MC2)=4/14；P(LC2)=3/14；

P(H

|

C1)=2/5；P(M|C1)=2/5；P(L|C1)=1/5；P(H

|

C2)=2/9；P(M|C2)=4/9；P(L|C2)=3/9；

属性a3：P(NC

1

)=4/14；P(YC1)=1/14；P(NC2)=3/14；P(YC2)=6/14；

P(N

|

C1)=4/5；P(Y|C1)=1/5；P(N

|

C2)=3/9；P(Y|C2)=6/9；

属性a4：P(FC

1

)=2/14；P(EC1)=3/14；P(FC2)=6/14；P(EC2)=3/14；

P(F

|

C1)=2/5；P(E|C1)=3/5；P(F

|

C2)=6/9；P(E|C2)=3/9；

测试：

1.设X={(<30),medium,no,fair}为待分类项，

2.计算

$P(X|C_{i})P(C_{i})=P(a_{1}|C_{i})P(a_{2}|C_{i})...P(a_{k}|C_{i})P(C_{i})=P(C_{i})\prod_{j=1}^{m}P(a_{j}|C_{i})$

P(X|C1)P(C1)=

P(a1|C1)*

P(a2|C1)*

P(a3|C1)*

P(a4|C1)P(C1)

=P(Tw|C1)*P(M|C1)*P(N

|

C1)*P(F

|

C1)*P(C1)=(3/5)*(2/5)*(4/5)*(2/5)*(5/14)= 0.0274;

P(X|C2)P(C2)=P(a1|C2)*P(a2|C2)*P(a3|C2)*P(a4|C2)P(C2)

=P(Tw|C2)*P(M|C2)*P(N

|

C2)*P(F

|

C2)*P(C2)=(2/9)*(4/9)*(3/9)*(6/9)*(9/14)= 0.0141;

3.根据贝叶斯定理求后验概率

$P(C_{i}|X)=\frac{P(C_{i}X)}{P(X)}=\frac{P(X|C_{i})P(C_{i})}{P(X)}$

，得到X属于C

_i

类别的后验概率；根据最大后验概率判断所属类别。

P(C

_α

|X)=max{P(C
_i
|X)}

$C_{\alpha }\in Y$

，则测试样本属于C
_α

P(X|C1)P(C1)>P(X|C2)P(C2)==>P(C1|X)>P(C2|X),

所以，此人不买电脑的概率大。

五、程序

1.这里只给出main函数部分，因为这个程序也是本人在网上下载别人的，可以验证，程序运行结果与计算结果相同

地址：http://download.csdn.net/download/theone_jie/9464087

//朴素贝叶斯分类器程序
#include <cstdio>
#include <Windows.h>
#include "LBayesClassifier.h"

const int NUM =14;  //训练样本个数
const int Dim =4;   //训练样本的维数

int main()
{
    /*定义样本矩阵
    每一行代表一个样本
    第一列为age,第二列为income,第3列为student,第4列为credit_rating
    把个属性进行了数字化,(<=30:20)、(31-40:30)、(>40:40)；
	(high:3)(medium:2)(low:1)；(no:0)(yes:1)；(fair:0)(excellent:1)
	*/
    int dataList[NUM*Dim] = 
	{   20,3,0,0,
		20,3,0,1,
		30,3,0,0,
		40,2,0,0,
		40,1,1,0,
		40,1,1,1,
		30,1,1,1,
		20,2,0,0,
		20,1,1,0,
		40,2,1,0,
		20,2,1,1,
		30,2,0,1,
		30,3,1,0,
		40,2,0,1}; 
    LBayesMatrix sampleMatrix(NUM, Dim, dataList);

    //定义样本的类别向量(0:不买电脑；1:买电脑)
    int classList[NUM] = {0,0,1,1,1,0,1,0,1,1,1,1,1,0};
    LBayesMatrix classVector(NUM, 1, classList);

    //定义贝叶斯原始问题
    LBayesProblem problem(sampleMatrix, classVector, BAYES_FEATURE_CONTINUS);

    //定义贝叶斯分类器, 并且训练
    LBayesClassifier classifier;
    classifier.TrainModel(problem);

    //输入新样本, 并预测新样本的类别
    LBayesMatrix newSample(1, Dim);
    newSample[0][0] = 20; 
	newSample[0][1] = 2; 
	newSample[0][2] = 0;
    newSample[0][3] = 0;
    int predictValue ; 
    classifier.Predict(newSample, &predictValue);

    printf("%d\n", predictValue);
    system("pause");
    return 0;
}

2.

最后在附加了opencv自带的正态贝叶斯分类器

//opencv自带正态贝叶斯分类器(Normal Bayes Classifier)
#include "opencv2/ml/ml.hpp"

using namespace std;  
using namespace cv;  
const int NUM=14;   //训练样本的个数
const int D=4;     //维度
//14个维数为4的训练样本集
double inputArr[NUM][D] =   
					{  20,3,0,0,
					   20,3,0,1,
					   30,3,0,0,
					   40,2,0,0,
					   40,1,1,0,
					   40,1,1,1,
					   30,1,1,1,
					   20,2,0,0,
					   20,1,1,0,
					   40,2,1,0,
					   20,2,1,1,
					   30,2,0,1,
					   30,3,1,0,
					   40,2,0,1};  
  
//一个测试样本的特征向量  
double testArr[]={20,3,0,0};  
  
int main()  
{  
    Mat trainData(NUM, D, CV_32FC1);//构建训练样本的特征向量  
    for (int i=0; i<NUM; i++)  {  
        for (int j=0; j<D; j++)  {  
            trainData.at<float>(i, j) = inputArr[i][j+1];  
        }  
    }  
    Mat trainResponse=(Mat_<float>(NUM,1)<<
		0,0,1,1,1,0,1,0,1,1,1,1,1,0);//构建训练样本的类别标签  
   
    CvNormalBayesClassifier Mybayes;  
    bool trainFlag = Mybayes.train(trainData, trainResponse);//进行贝叶斯分类器训练  
    if (trainFlag)  {  
        cout<<"train over..."<<endl;  
        Mybayes.save("normalBayes.txt");  
    }  
    else  {  
        cout<<"train error..."<<endl;  
        system("pause");  
        exit(-1);  
    }  
    CvNormalBayesClassifier Tbayes;  
    Tbayes.load("normalBayes.txt");  
  
    Mat testSample(1, D, CV_32FC1);//构建测试样本  
    for (int i=0; i<D; i++)  {  
        testSample.at<float>(0, i) = testArr[i];  
    }    
    float flag = Tbayes.predict(testSample);//进行测试  
    cout<<"flag = "<<flag<<endl;  
    system("pause");  
    return 0;  
}

本人能力有限，难免有出错的地方。敬请赐教

更多资源：http://blog.csdn.net/lavorange/article/details/17841383

原文链接：https://blog.csdn.net/u012507022/article/details/51763008

你可能也喜欢