基础知识

求导公式

范德蒙行列式

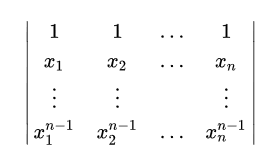
变限积分函数求导公式：

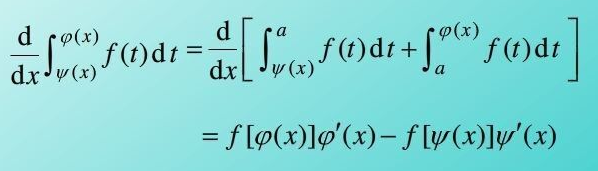
多元函数微分学

领域

：空间一点的周围很小的部分

空心领域

：空间一点的周围很小的部分，不含这点

D

：一片指定的区域

内点

：一点存在领域在D内

边界点

：一点所有领域都存在属于D和不属于D，点可在D上D内D外

边界

：D的边界点集合

外点

:存在领域不在D内

聚点

：所有领域都要有D内非P的点

开集

：D中每个点都是内点

开区域

：无边

闭区域

：有边

n元函数

：R^n的一个子集

等值线

：相当于地图等高线

heinz归结原则

：当P以任何方式趋于Po时，极限相同

区域

：无孤立点

区域

：相当于一元函数的定义域和值域等

一元函数

：一条曲线到一个数集上的映射

多元函数

：平面、空间至更高维度区域到一个数集上的映射

初等函数

：基本初等函数通过有限次四则运算、复合组成的可用解析式写出的函数

多元函数的极限：

两种方法判断不存在

①

以一种解析式接近时极限不存在

，y=kx，y=x，
$y=\frac{1}{2}x$
，
$y=kx^2$
，
$x=ky^2$
（目的是让x或者y的次数相同，从而消去x或者y）

②以两种不同的解析式接近时极限不同

四种方法求出极限

①极限定义

②

无穷小与有限函数的乘积为0

③多元函数换元成一元函数

④夹逼准则

其它方法求极限

多元函数化成一元函数：同乘同除一个变量，用等价无穷小消去另一个变量
多元初等函数直接代入极限
两种重要极限：化为e

多元函数的连续和间断

连续

：D内聚点，极限=值，同求极限的方法

不连续

：极限不存在或无定义

连续定理

：所有初等多元函数在定义域内都是连续的

间断点

：不在定义域内的一切点

有界闭区域多元性质：最大最小值定理：

在定义域内最大最小值至少出现一次

有界闭区域多元性质：介值定理：

在不同两点间，一定存在一点值在这两个值之间

偏导数

：对x偏导，就将其它字母看成常数，然后求导（

注意：如果指数和底数同时存在自变量，要把指数函数两边求In再两边求导

）

混合二阶偏导数

：注意分母的顺序，虽然顺序不影响偏导结果

一元函数微分，可微

：y=f(x)
$\Delta y=A\Delta x+o(\Delta x)$
$dy=A\Delta x=f{}'(x)dx$

多元函数微分，可微

：z=f(x,y)
$\Delta z=A\Delta x+B\Delta y+o(\rho )$
$\rho =\sqrt{\Delta x^2+\Delta y^2}$
$dz=\frac{\delta z}{\delta x}dx+\frac{\delta z}{\delta y}dy$

判断在一点(a,b)可微的步骤

:1.求出在这点的偏导数 2.令

$\rho =\sqrt{x^2+ y^2}$
$\Delta z=f(x,y)-f(a,b)$
3.求极限
$lim\varrho ->0\frac{\Delta z-xianxingzhubu}{\varrho }=0$
则可微

偏增量

：一个自变量不变，另一个变

偏导数

：定义
$\Delta x->0$
的极限下，x的偏增量除以
$\Delta x$
；

只有分段函数在分段点的偏导用定义，不然就用求导代值的方法

用定义求一点偏导

：

$f_{x}(0,0)=lim\frac{f(\Delta x,0)-f(0,0)}{\Delta x}$

，两点直接代值

z=f(x,y)+f(x+y)求z对x，z对y的偏导

：相当于一元函数求导，

f（x，y）对x求偏导，f加撇，乘y，对y求偏导，f加撇，乘x；

f（x+y）对x求偏导，对y求偏导，f加撇

f（x,g(y)）对x求偏导，f加撇，对y求偏导，f加撇，乘
$g{}'(y)$
；

全偏量

：两个自变量同时发生改变

全微分：

$dz=\frac{\delta z}{\delta x}dx+\frac{\delta z}{\delta y}dy$

可微则可导，连续

一元函数：可微=可导

多元函数：可微-》可导

在一点存在连续的偏导数则可微

偏导在一点的极限不存在，则不连续，则不可微

多元初等函数在定义域内可微

函数偏导与连续性的关系

一元函数：

可导一定连续，连续不一定可导

多元函数：

可导不一定连续，连续不一定可导

偏导数的几何意义

f(x,y)是空间中的不规则曲面，上面存在一点P(
$x_{0},y_{0}$
)，关于P点对x的偏导数的几何意义为

平行于xoz平面的平面与f(x,y)交一条曲线

P点对x的偏导数就是这条曲线上P点的切线

证明连续

：极限的△X△Y趋近0，全增量=0，当y以一种解析式趋近(0,0)，极限全增量，代换，判断存在不存在

cos1/x和sin1/x不存在

证明偏导存在

：偏增量/△X极限存在

偏导存在且有界，则连续

多元复合函数的求导

多元复合显示函数

：只有自变量，不含中间变量，直接求导

多元复合抽象函数

：z=f(u，v)，有多少个中间变量，有几项只和

求导的链式法则

：对的偏导=两项相加

半导数

：只有一个中间变量

全导数

：只有一个自变量

特殊情况

：z=f(u,v,y) u=u(x,y) v=v(x,y)

fx=两项和

fy=三项和（第三项∂f/∂y）

特殊情况

：u=f(x,y,z) z=g(y,t) t=h(x,y) u和z的偏导都要求，将z的偏导代入可得答案

特殊情况

：z=y/f(g(x,y)) 偏导=商的求导

极坐标P29

一元全微分形式不变性

全微分运算公式

①+②×③÷

复合函数的高阶偏导数

：两次链式法则，第二次非x的系数不变，若系数含x则为乘法求导法则，f变为
$\frac{\vartheta f}{\vartheta x}$
再链式