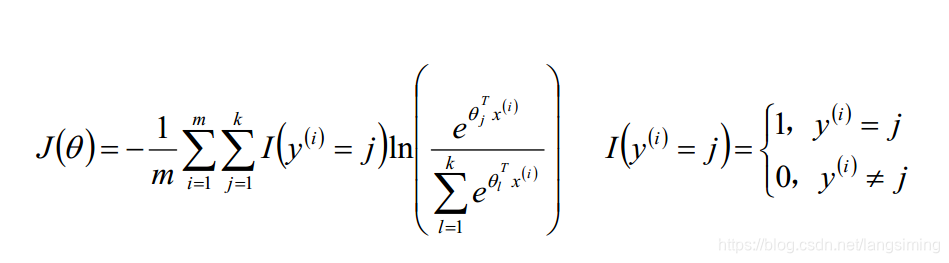回归算法

Post author:xfxia
Post published:2023年9月1日
Post category:其他

1. 什么是回归算法

回归算法是监督型算法的一种，通过利用测试集数据来建立模型，再利用这个模型训练集中的数据进行处理的算法。线性回归旨在寻找到一根线，这个线到到达所有样本点的距离的和是最小的。常用在预测和分类领域。

2. 线性回归中经常使用的两种算法

a. 最小二乘法

公式：
$\Theta = (X^{T}X)^{-1}X^{T}Y$

推导过程：见博文：

https://blog.csdn.net/qq_27576655/article/details/82218489

b. 梯度下降法

利用迭代的思想，不断的更新θ值，最终θ会收缩到某个值上。

θ的变化公式：
$\Theta =\Theta -\alpha\cdot \frac{\partial J(\Theta )}{\partial \Theta }$

α为步长，学习率

详情见下面链接：

https://blog.csdn.net/yato0514/article/details/82261821

使用梯度下降法的过程中如果遇到局部最优解应该怎么办？

学习率的选择是否正确：学习率过大容易跳过最优解，学习率过小迭代速度又会非常慢。

算法初始值的选择：初始值不同，θ最终收敛的值会不同。所以一般会取多个不同的θ值进行试验，最后选损失函数最小的那个值。

标准化：不同的特征的取值范围不同，他们收敛的速度也会不一样，为了减少特征值取值的影响，尽量需要标准化。

c. 局部加权回归后面了解

3. 如何解决线性回归中的过拟合现象

过拟合产生的原因是因为θ值过多或者是θ值过哦大造成的，解决方法可以使用L1正则（又称为lasso回归）或者L2正则

（又称为ridge回归，岭回归）或者elastic net(弹性网络)算法

L1正则公式如下,其中 λ>0

$J(\Theta )=\frac{1}{2}\sum_{i=1}^{m}(h_{\Theta }(x_{i} )-y_{i})^{2}+\lambda \sum_{j=1}^{n}\left |\Theta _{j} \right |$

L2正则公式如下：其中 λ>0

$J(\Theta )=\frac{1}{2}\sum_{i=1}^{m}(h_{\Theta }(x_{i} )-y_{i})^{2}+\lambda \sum_{j=1}^{n}\Theta_{j}^{2}$

elastic net公式如下：其中 λ>0，p在[0,1]之间

$J(\Theta )=\frac{1}{2}\sum_{i=1}^{m}(h_{\Theta }(x_{i} )-y_{i})^{2}+\lambda( \rho \sum_{j=1}^{n}\left | \Theta _{j} \right |+ (1-\rho )\sum_{j=1}^{n}\Theta_{j}^{2})$

特点：Ridge模型具有较高的准确性、鲁棒性以及稳定性,不会丢失特征；LASSO模型具有较高的求解

速度（会丢失特征）；elastic net 综合两者的优点

4. 模型效果判断

取值范围(负无穷,1]，值越大表示模型越拟合训练数据；最优解是1；当模型

预测为随机值的时候，有可能为负；

5. 机器学习调参

在实际工作中，对于各种算法模型(线性回归)来讲，我们需要获取θ、λ、p的值；θ的求解其实就是算法模型的求解，一般不需要开发人员参与(算法已经实现)，主要需要求解的是λ和p的值，这个过程就叫做调参(超参)

交叉验证：将训练数据分为多份，其中一份进行数据验证并获取最优的超参：λ和p；比如：十折交叉验证、五折交叉验证(scikit-learn中默认)等

6. 分类算之逻辑回归算法

logistic回归

a. 因变量转换公式

$h(\Theta )=g(\Theta _{0}x_{0}+\Theta _{1}x_{1}+\Theta _{2}x_{2})$
->
$g(h(\Theta ))=\frac{1}{1+e^{-h(\Theta )}}$

损失函数如下：

softmax回归

用于多元分类

它的因变量转换公式：

损失函数：损失函数中会求一个预测值到其他类型间的误差，将被转换的因变量对数化，作为这个误差值。

原文链接：https://blog.csdn.net/langsiming/article/details/94327925

你可能也喜欢