博客

完全背包问题：给定一个背包，容量为capacity。给定一堆物品，物品的价值和重量存在数组当中，具体如下：

int[] w = {2, 3, 4, 5};   //物品重量
int[] v = {3, 4, 5, 6};   //物品价值
int capacity = 8;         //背包容量

与0-1背包不同的是，对每一种物品，它可以放入无限多件。

考虑到每一个物品，它都有两种决策：放或者不放；如果放的话，放多少件

可以放入背包的前提是 w[i]<=capacity

对于每个物品，如果可以放入背包，即满足 w[i]<=capacity 条件，背包的价值就会在以下两个情况间选择较大值：

1. 当前物品放入背包：因为已经确定了当前物品 i 是要放入，对于放几件的问题，用当前的背包容量减去当前物品的重量，再找到前 i 种物品放入背包容量为 capacity-w[i] 的价值，加上当前物品的价值 v[i]

2. 当前物品不放入背包：总价值 = 前 i-1 种物品放入capacity背包中的价值

归结成符号语言

total = max(value[i - 1][capacity], value[i][capacity - w[i]] + v[i]);

如果不满足 w[i]<=capacity ，就无法放入背包，等同于上述情况2，此时归结为符号语言

total = value[i - 1][capacity]

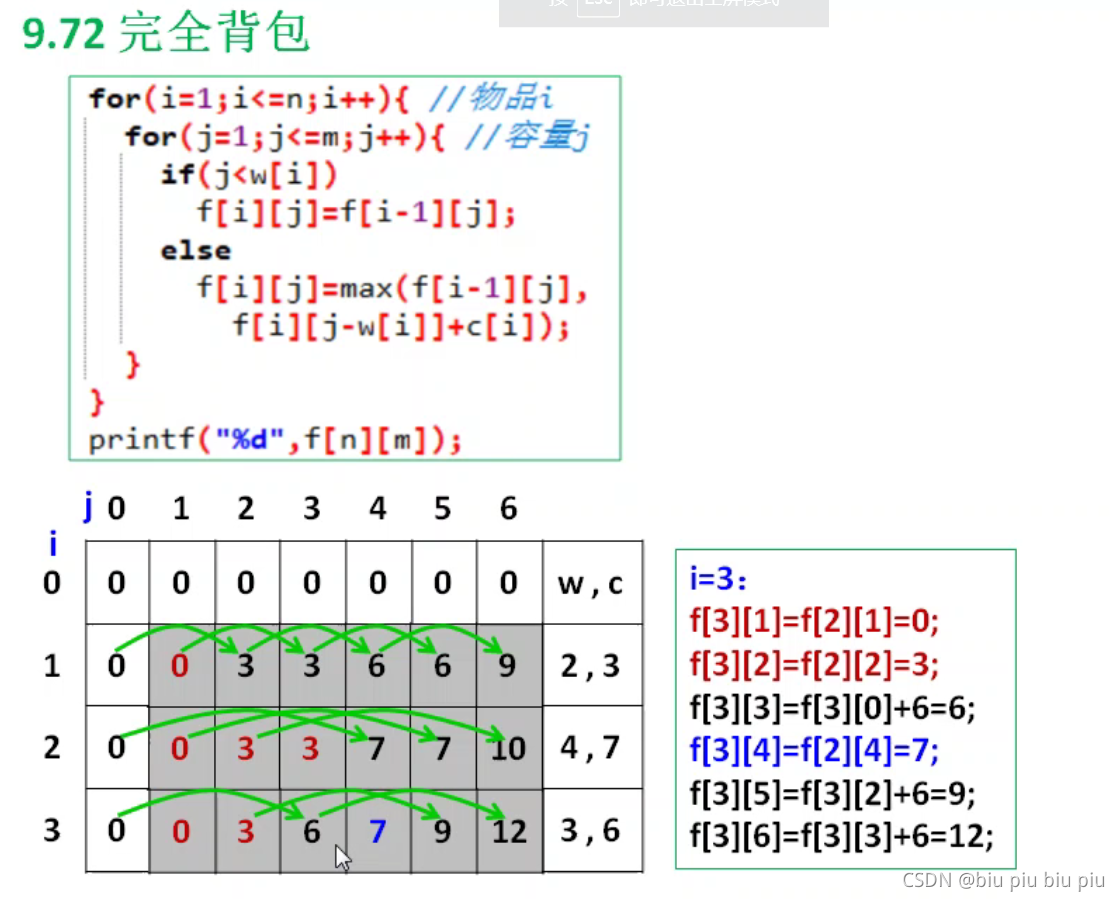
0-1背包我们计算当前行时，是通过上一行转移来的，完全背包因为可以放入多件当前物品，所以当前状态是从上一行和当前行转移来的。

完整代码

public class 完全背包 {
    public static int[][] dp;
    public static int[] item;
    public static int[] w;
    public static int[] v;
    public static void main(String[] args) {
        w = new int[]{2, 3, 4, 5};
        v = new int[]{3, 4, 5, 6};
        int capacity = 8;
        int num = w.length;
        dp = new int[num + 1][capacity + 1];
        item = new int[num + 1];
        for (int i = 1; i <= num; i++) {
            for (int j = 1; j <= capacity; j++) {
                if (j >= w[i - 1]) {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - w[i - 1]] + v[i - 1]);
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        System.out.println(dp[num][capacity]);
    }
}

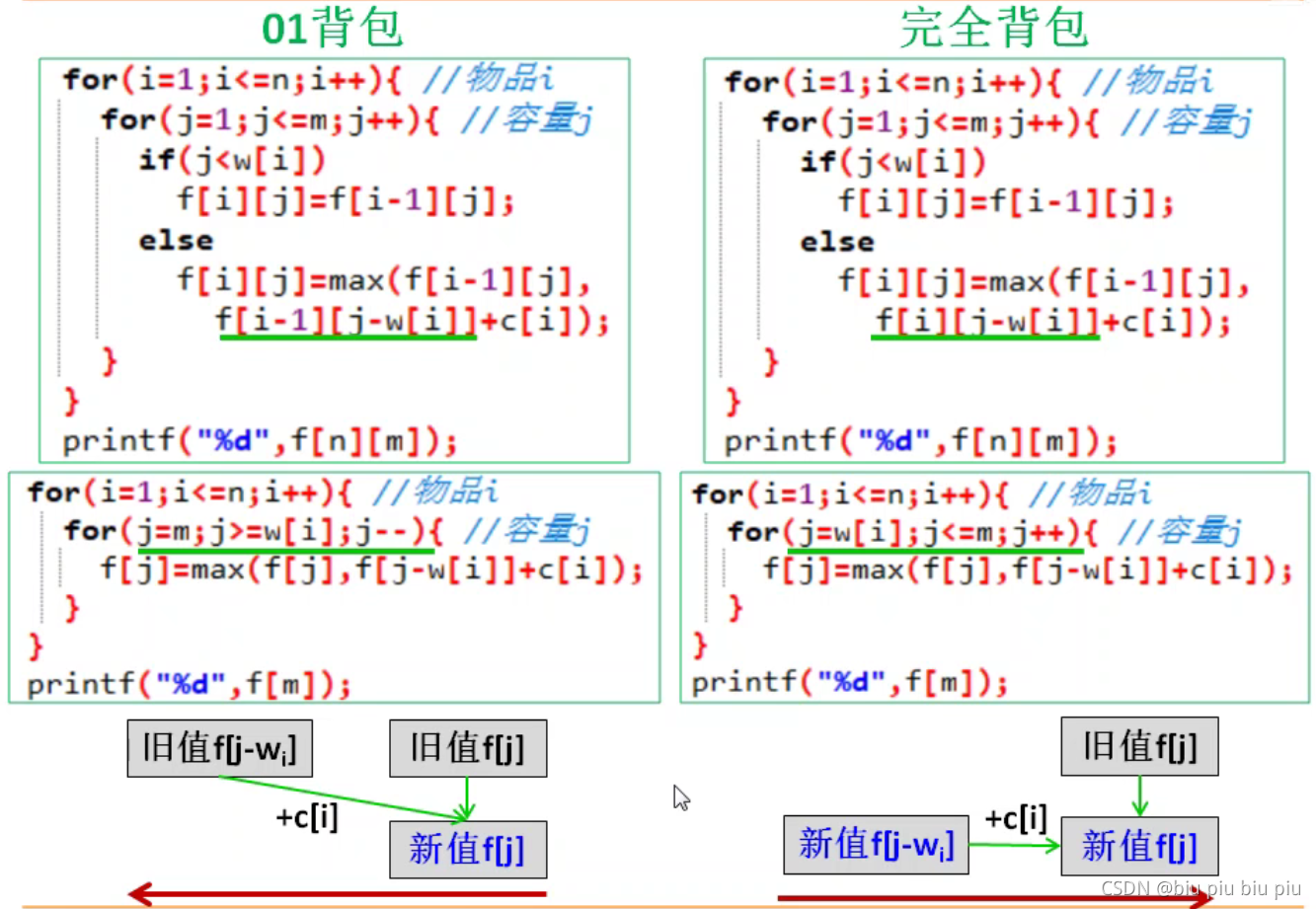
由于每一行的更新只与当前行和上一行有关，可以将空间由二维压缩为一维