(隐函数存在定理-1)
设二元函数
F
(
x
,
y
)
在点
(
x
0
,
y
0
)
的邻域
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内满足以下条件:
设二元函数F(x,y)在点(x_0,y_0)的邻域U(x_0,\delta)\times U(y_0,\delta)\ (\delta >0)内满足以下条件:
设二元函数
F
(
x
,
y
)
在点
(
x
0
,
y
0
)
的邻域
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内满足以下条件:
(
1
)
F
(
x
0
,
y
0
)
=
0
(1) F(x_0,y_0)=0
(
1
)
F
(
x
0
,
y
0
)
=
0
;
(
2
)
F
(
x
,
y
)
、
F
y
(
x
,
y
)
在
U
(
(
x
0
,
y
0
)
,
δ
)
(
δ
>
0
)
内连续
(2) F(x,y)、F_y(x,y)在U((x_0,y_0),\delta) (\delta >0)内连续
(
2
)
F
(
x
,
y
)
、
F
y
(
x
,
y
)
在
U
((
x
0
,
y
0
)
,
δ
)
(
δ
>
0
)
内连续
;
(
3
)
F
y
(
x
0
,
y
0
)
≠
0
(3) F_y(x_0,y_0)\ne 0
(
3
)
F
y
(
x
0
,
y
0
)
=
0
;
则
∃
δ
0
∈
(
0
,
δ
)
使得在
U
(
x
0
,
δ
0
)
内唯一存在满足下述条件的连续函数
y
=
f
(
x
)
:
则 \exists \ \delta_0 \in(0,\delta)使得在U(x_0,\delta_0)内唯一存在满足下述条件的连续函数y=f(x):
则
∃
δ
0
∈
(
0
,
δ
)
使得在
U
(
x
0
,
δ
0
)
内唯一存在满足下述条件的连续函数
y
=
f
(
x
)
:
(
a
)
y
0
=
f
(
x
0
)
;
(a) y_0=f(x_0);
(
a
)
y
0
=
f
(
x
0
)
;
(
b
)
对
∀
x
∈
U
(
x
0
,
δ
0
)
,
F
(
x
0
,
f
(
x
0
)
)
=
0
(b)对\forall x\in U(x_0,\delta_0),F(x_0,f(x_0))=0
(
b
)
对
∀
x
∈
U
(
x
0
,
δ
0
)
,
F
(
x
0
,
f
(
x
0
))
=
0
(
c
)
若
F
x
(
x
,
y
)
在
U
(
(
x
0
,
y
0
)
,
δ
)
(
δ
>
0
)
内连续则
y
=
f
(
x
)
存在连续导数,且
f
′
(
x
)
=
−
F
x
F
y
。
(c)若F_x(x,y)在U((x_0,y_0),\delta) (\delta >0)内连续则y=f(x)存在连续导数,且f'(x)=-\frac{F_x}{F_y}。
(
c
)
若
F
x
(
x
,
y
)
在
U
((
x
0
,
y
0
)
,
δ
)
(
δ
>
0
)
内连续则
y
=
f
(
x
)
存在连续导数,且
f
′
(
x
)
=
−
F
y
F
x
。
证明:
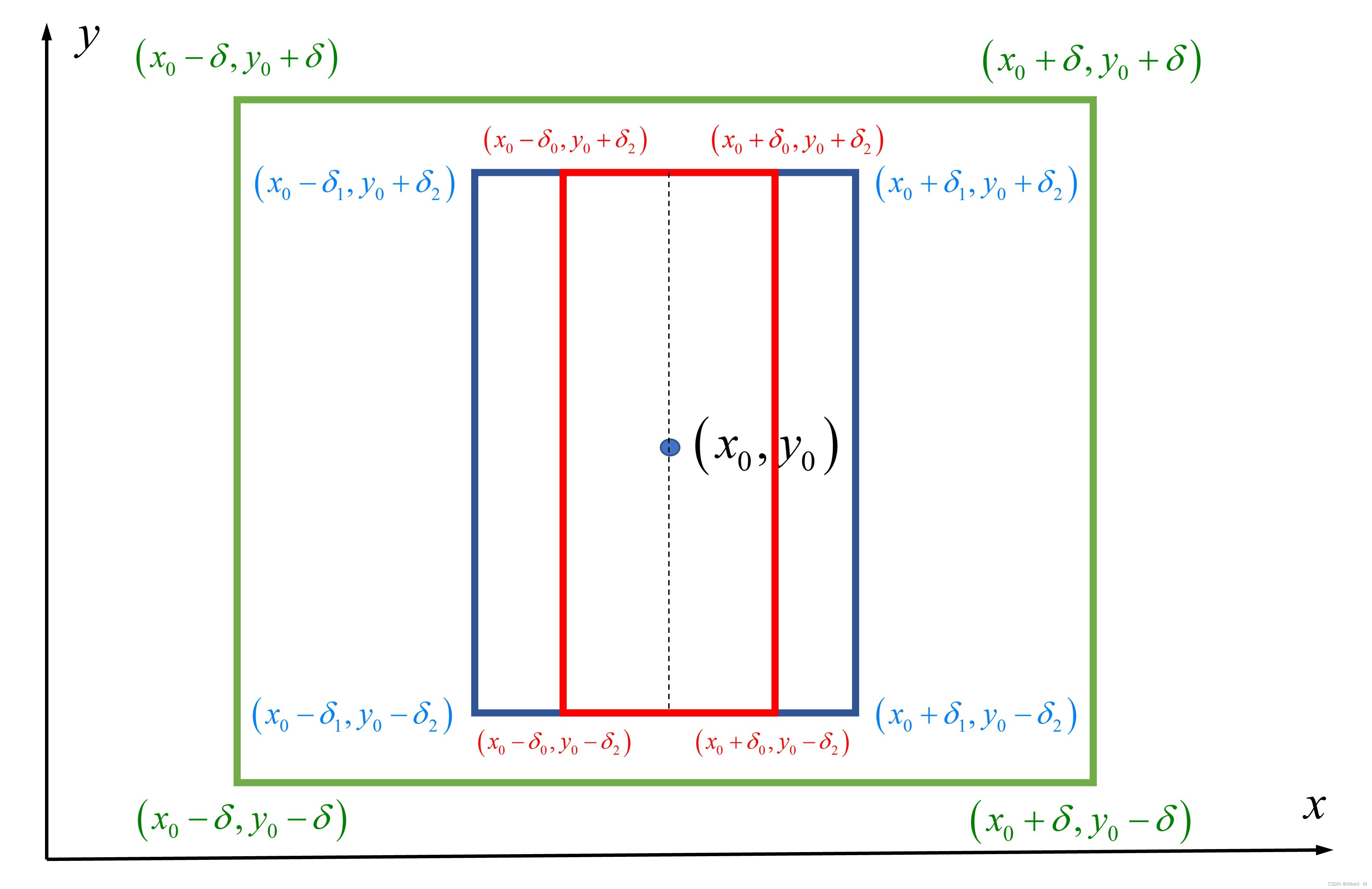
不妨假设
F
y
(
x
0
,
y
0
)
>
0
F_y(x_0,y_0)>0
F
y
(
x
0
,
y
0
)
>
0
,而
F
y
(
x
0
,
y
0
)
<
0
F_y(x_0,y_0)<0
F
y
(
x
0
,
y
0
)
<
0
的情形相当于对
F
′
(
x
,
y
)
=
−
F
(
x
,
y
)
F'(x,y)=-F(x,y)
F
′
(
x
,
y
)
=
−
F
(
x
,
y
)
进行相关讨论。
又由
F
y
(
x
,
y
)
在
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
F_y(x,y)在U(x_0,\delta)\times U(y_0,\delta)\ (\delta >0)
F
y
(
x
,
y
)
在
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内的连续性可知:
∃
δ
1
,
δ
2
∈
(
0
,
δ
)
s
.
t
.
对
∀
(
x
,
y
)
∈
U
(
x
0
,
δ
1
)
×
U
(
y
0
,
δ
2
)
,均有
F
y
(
x
,
y
)
>
0
\exists \delta_1,\delta_2\in(0,\delta)\ s.t.\ 对\forall(x,y)\in U(x_0,\delta_1)\times U(y_0,\delta_2),均有F_y(x,y)>0
∃
δ
1
,
δ
2
∈
(
0
,
δ
)
s
.
t
.
对
∀
(
x
,
y
)
∈
U
(
x
0
,
δ
1
)
×
U
(
y
0
,
δ
2
)
,均有
F
y
(
x
,
y
)
>
0
特别地,对
∀
y
∈
U
(
y
0
,
δ
2
)
\forall y\in U(y_0,\delta_2)
∀
y
∈
U
(
y
0
,
δ
2
)
均有
F
y
(
x
0
,
y
)
>
0
F_y(x_0,y)>0
F
y
(
x
0
,
y
)
>
0
,即:
固定
x
=
x
0
,则函数
F
(
x
0
,
y
)
在
y
∈
U
(
y
0
,
δ
2
)
内单调递增
固定x=x_0,则函数 F(x_0,y)在y\in U(y_0,\delta_2)内单调递增
固定
x
=
x
0
,则函数
F
(
x
0
,
y
)
在
y
∈
U
(
y
0
,
δ
2
)
内单调递增
又因为,
F
(
x
0
,
y
0
)
=
0
F(x_0,y_0)=0
F
(
x
0
,
y
0
)
=
0
,则:
{
F
(
x
0
,
y
0
+
δ
2
)
>
0
F
(
x
0
,
y
0
−
δ
2
)
<
0
\begin{cases}F(x_0,y_0+\delta_2)>0\\F(x_0,y_0-\delta_2)<0\end{cases}
{
F
(
x
0
,
y
0
+
δ
2
)
>
0
F
(
x
0
,
y
0
−
δ
2
)
<
0
进一步由
F
(
x
,
y
)
在
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
F(x,y)在U(x_0,\delta)\times U(y_0,\delta)\ (\delta >0)
F
(
x
,
y
)
在
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内的连续性可知:
∃
δ
0
∈
(
0
,
δ
1
)
s
.
t
.
对
∀
x
∈
U
(
x
0
,
δ
0
)
,均有
{
F
(
x
,
y
0
+
δ
2
)
>
0
F
(
x
,
y
0
−
δ
2
)
<
0
\exists\delta_0\in(0,\delta_1)\ s.t.\ 对\forall x\in U(x_0,\delta_0),均有\begin{cases}F(x,y_0+\delta_2)>0\\F(x,y_0-\delta_2)<0\end{cases}
∃
δ
0
∈
(
0
,
δ
1
)
s
.
t
.
对
∀
x
∈
U
(
x
0
,
δ
0
)
,均有
{
F
(
x
,
y
0
+
δ
2
)
>
0
F
(
x
,
y
0
−
δ
2
)
<
0
换而言之,
对任意
x
˜
∈
U
(
x
0
,
δ
0
)
均有
F
(
x
˜
,
y
)
由负数
F
(
x
˜
,
y
−
δ
2
)
连续单调地增长为正数
F
(
x
˜
,
y
+
δ
2
)
对任意\~x\in U(x_0,\delta_0)均有F(\~x,y)由负数F(\~x,y-\delta_2)连续单调地增长为正数F(\~x,y+\delta_2)
对任意
x
˜
∈
U
(
x
0
,
δ
0
)
均有
F
(
x
˜
,
y
)
由负数
F
(
x
˜
,
y
−
δ
2
)
连续单调地增长为正数
F
(
x
˜
,
y
+
δ
2
)
故由零点定理可知:
对
∀
x
˜
∈
U
(
x
0
,
δ
0
)
均唯一
∃
y
˜
∈
U
(
y
0
,
δ
2
)
s
.
t
.
F
(
x
˜
,
y
˜
)
=
0
对\forall\~x\in U(x_0,\delta_0)\ 均唯一\ \exists\~y\in U(y_0,\delta_2)\ s.t.\ F(\~x,\~y)=0
对
∀
x
˜
∈
U
(
x
0
,
δ
0
)
均唯一
∃
y
˜
∈
U
(
y
0
,
δ
2
)
s
.
t
.
F
(
x
˜
,
y
˜
)
=
0
上述讨论证明了隐函数
y
˜
=
f
(
x
˜
)
\~y=f(\~x)
y
˜
=
f
(
x
˜
)
的唯一存在性,接下来说明隐函数的连续性:
取
x
^
∈
U
(
x
0
,
δ
0
)
\hat{x}\in U(x_0,\delta_0)
x
^
∈
U
(
x
0
,
δ
0
)
,
y
^
=
f
(
x
^
)
\hat{y}=f(\hat{x})
y
^
=
f
(
x
^
)
,则对充分小
ε
>
0
\varepsilon>0
ε
>
0
有:
{
F
(
x
^
,
y
^
+
ε
)
>
0
F
(
x
^
,
y
^
−
ε
)
<
0
\begin{cases}F(\hat{x},\hat{y}+\varepsilon)>0\\F(\hat{x},\hat{y}-\varepsilon)<0\end{cases}
{
F
(
x
^
,
y
^
+
ε
)
>
0
F
(
x
^
,
y
^
−
ε
)
<
0
又由
F
(
x
,
y
)
F(x,y)
F
(
x
,
y
)
在
(
x
^
,
y
^
−
ε
)
、
(
x
^
,
y
^
+
ε
)
(\hat{x},\hat{y}-\varepsilon)、(\hat{x},\hat{y}+\varepsilon)
(
x
^
,
y
^
−
ε
)
、
(
x
^
,
y
^
+
ε
)
处的连续性可知:
∃
δ
′
∈
(
0
,
δ
0
)
s
.
t
.
对
∀
x
∈
U
(
x
0
,
δ
′
)
⊂
U
(
x
0
,
δ
0
)
,
均有
{
F
(
x
,
y
^
+
ε
)
>
0
F
(
x
,
y
^
−
ε
)
<
0
⟹
{
y
^
+
ε
>
f
(
x
)
y
^
−
ε
<
f
(
x
)
⟹
∣
y
^
−
f
(
x
)
∣
<
ε
\exists \delta’\in(0,\delta_0)\ s.t.\ 对\forall x\in U(x_0,\delta’)\subset U(x_0,\delta_0),均有\begin{cases}F(x,\hat{y}+\varepsilon)>0\\F(x,\hat{y}-\varepsilon)<0\end{cases}\Longrightarrow \begin{cases}\hat{y}+\varepsilon>f(x)\\\hat{y}-\varepsilon<f(x)\end{cases}\Longrightarrow |\hat{y}-f(x)|<\varepsilon
∃
δ
′
∈
(
0
,
δ
0
)
s
.
t
.
对
∀
x
∈
U
(
x
0
,
δ
′
)
⊂
U
(
x
0
,
δ
0
)
,
均有
{
F
(
x
,
y
^
+
ε
)
>
0
F
(
x
,
y
^
−
ε
)
<
0
⟹
{
y
^
+
ε
>
f
(
x
)
y
^
−
ε
<
f
(
x
)
⟹
∣
y
^
−
f
(
x
)
∣
<
ε
故,
∀
ε
>
0
,
∃
δ
′
>
0
,
s
.
t
.
∀
x
∈
U
(
x
^
,
δ
′
)
:
∣
f
(
x
)
−
y
^
∣
<
ε
\forall \varepsilon>0,\exists\delta’>0,\ s.t.\ \forall x\in U(\hat{x},\delta’):|f(x)-\hat{y}|<\varepsilon
∀
ε
>
0
,
∃
δ
′
>
0
,
s
.
t
.
∀
x
∈
U
(
x
^
,
δ
′
)
:
∣
f
(
x
)
−
y
^
∣
<
ε
符合隐函数连续性的定义。
下面证明:若
F
x
(
x
,
y
)
F_x(x,y)
F
x
(
x
,
y
)
在
U
(
(
x
0
,
y
0
)
,
δ
)
(
δ
>
0
)
U((x_0,y_0),\delta) (\delta >0)
U
((
x
0
,
y
0
)
,
δ
)
(
δ
>
0
)
内连续则
y
=
f
(
x
)
y=f(x)
y
=
f
(
x
)
存在连续导数。
任取
x
ˉ
∈
U
(
x
0
,
δ
0
)
\bar{x}\in U(x_0,\delta_0)
x
ˉ
∈
U
(
x
0
,
δ
0
)
与充分小的增量
Δ
x
,
s
.
t
.
x
ˉ
+
Δ
x
∈
U
(
x
0
,
δ
0
)
\Delta x,s.t.\ \bar{x}+\Delta x\in U(x_0,\delta_0)
Δ
x
,
s
.
t
.
x
ˉ
+
Δ
x
∈
U
(
x
0
,
δ
0
)
,记:
y
ˉ
=
f
(
x
ˉ
)
,
Δ
y
=
f
(
x
ˉ
+
Δ
x
)
−
f
(
x
ˉ
)
\bar{y}=f(\bar{x}),\Delta y=f(\bar{x}+\Delta x)-f(\bar{x})
y
ˉ
=
f
(
x
ˉ
)
,
Δ
y
=
f
(
x
ˉ
+
Δ
x
)
−
f
(
x
ˉ
)
由于
F
(
x
ˉ
,
f
(
x
ˉ
)
)
=
0
,
F
(
x
ˉ
+
Δ
x
,
f
(
x
ˉ
+
Δ
x
)
)
=
0
F(\bar{x},f(\bar{x}))=0,F(\bar{x}+\Delta x,f(\bar{x}+\Delta x))=0
F
(
x
ˉ
,
f
(
x
ˉ
))
=
0
,
F
(
x
ˉ
+
Δ
x
,
f
(
x
ˉ
+
Δ
x
))
=
0
,则由拉格朗日微分中值定理:
0
=
F
(
x
ˉ
+
Δ
x
,
f
(
x
ˉ
+
Δ
x
)
)
−
F
(
x
ˉ
,
f
(
x
ˉ
)
)
=
F
(
x
ˉ
+
Δ
x
,
y
ˉ
+
Δ
y
)
−
F
(
x
ˉ
,
y
ˉ
)
=
F
x
(
x
ˉ
+
θ
Δ
x
,
y
ˉ
+
θ
Δ
y
)
Δ
x
+
F
y
(
x
ˉ
+
θ
Δ
x
,
y
ˉ
+
θ
Δ
y
)
Δ
y
(
0
<
θ
<
1
)
0=F(\bar{x}+\Delta x,f(\bar{x}+\Delta x))-F(\bar{x},f(\bar{x}))=F(\bar{x}+\Delta x,\bar{y}+\Delta y)-F(\bar{x},\bar{y})=F_x(\bar{x}+\theta\Delta x,\bar{y}+\theta\Delta y)\Delta x+F_y(\bar{x}+\theta\Delta x,\bar{y}+\theta\Delta y)\Delta y\ (0<\theta<1)
0
=
F
(
x
ˉ
+
Δ
x
,
f
(
x
ˉ
+
Δ
x
))
−
F
(
x
ˉ
,
f
(
x
ˉ
))
=
F
(
x
ˉ
+
Δ
x
,
y
ˉ
+
Δ
y
)
−
F
(
x
ˉ
,
y
ˉ
)
=
F
x
(
x
ˉ
+
θ
Δ
x
,
y
ˉ
+
θ
Δ
y
)
Δ
x
+
F
y
(
x
ˉ
+
θ
Δ
x
,
y
ˉ
+
θ
Δ
y
)
Δ
y
(
0
<
θ
<
1
)
由于
F
y
≠
0
F_y\ne0
F
y
=
0
,则有:
Δ
y
Δ
x
=
−
F
x
(
x
ˉ
+
θ
Δ
x
,
y
ˉ
+
θ
Δ
y
)
F
y
(
x
ˉ
+
θ
Δ
x
,
y
ˉ
+
θ
Δ
y
)
\frac{\Delta y}{\Delta x}=-\frac{F_x(\bar{x}+\theta\Delta x,\bar{y}+\theta\Delta y)}{F_y(\bar{x}+\theta\Delta x,\bar{y}+\theta\Delta y)}
Δ
x
Δ
y
=
−
F
y
(
x
ˉ
+
θ
Δ
x
,
y
ˉ
+
θ
Δ
y
)
F
x
(
x
ˉ
+
θ
Δ
x
,
y
ˉ
+
θ
Δ
y
)
由
F
x
、
F
y
与
y
=
f
(
x
)
F_x、F_y与y=f(x)
F
x
、
F
y
与
y
=
f
(
x
)
的连续性:
lim
Δ
x
⟶
0
Δ
y
Δ
x
=
−
F
x
(
x
ˉ
,
y
ˉ
)
F
y
(
x
ˉ
,
y
ˉ
)
\lim_{\Delta x\longrightarrow0}\frac{\Delta y}{\Delta x}=-\frac{F_x(\bar{x},\bar{y})}{F_y(\bar{x},\bar{y})}
Δ
x
⟶
0
lim
Δ
x
Δ
y
=
−
F
y
(
x
ˉ
,
y
ˉ
)
F
x
(
x
ˉ
,
y
ˉ
)
Remark:
(1) 隐函数存在定理所确定的隐函数只是局部存在;
(2) 隐函数存在定理只给出了隐函数存在的充分条件,若不满足定理条件也可能存在隐函数。
作为上述定理的推广,由类似的推导可以得出:
(隐函数存在定理-2)
设函数
F
(
x
⃗
,
y
)
(
x
⃗
∈
R
n
)
在点
(
x
⃗
0
,
y
0
)
的邻域
U
(
x
⃗
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内满足以下条件:
设函数F(\vec{x},y)(\vec{x}\in R^n)在点(\vec{x}_0,y_0)的邻域U(\vec{x}_0,\delta)\times U(y_0,\delta)\ (\delta >0)内满足以下条件:
设函数
F
(
x
,
y
)
(
x
∈
R
n
)
在点
(
x
0
,
y
0
)
的邻域
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内满足以下条件:
(
1
)
F
(
x
⃗
0
,
y
0
)
=
0
(1) F(\vec{x}_0,y_0)=0
(
1
)
F
(
x
0
,
y
0
)
=
0
;
(
2
)
F
(
x
⃗
,
y
)
、
F
y
(
x
⃗
,
y
)
在
U
(
x
⃗
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内连续
(2) F(\vec{x},y)、F_y(\vec{x},y)在U(\vec{x}_0,\delta)\times U(y_0,\delta)\ (\delta >0)内连续
(
2
)
F
(
x
,
y
)
、
F
y
(
x
,
y
)
在
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内连续
;
(
3
)
F
y
(
x
⃗
0
,
y
0
)
≠
0
(3) F_y(\vec{x}_0,y_0)\ne 0
(
3
)
F
y
(
x
0
,
y
0
)
=
0
;
则
∃
δ
0
∈
(
0
,
δ
)
使得在
U
(
x
⃗
0
,
δ
0
)
内唯一存在满足下述条件的连续函数
y
=
f
(
x
⃗
)
:
则 \exists \ \delta_0 \in(0,\delta)使得在U(\vec{x}_0,\delta_0)内唯一存在满足下述条件的连续函数y=f(\vec{x}):
则
∃
δ
0
∈
(
0
,
δ
)
使得在
U
(
x
0
,
δ
0
)
内唯一存在满足下述条件的连续函数
y
=
f
(
x
)
:
(
a
)
y
0
=
f
(
x
⃗
0
)
;
(a) y_0=f(\vec{x}_0);
(
a
)
y
0
=
f
(
x
0
)
;
(
b
)
对
∀
x
⃗
∈
U
(
x
⃗
0
,
δ
0
)
,
F
(
x
⃗
0
,
f
(
x
⃗
0
)
)
=
0
(b)对\forall \vec{x}\in U(\vec{x}_0,\delta_0),F(\vec{x}_0,f(\vec{x}_0))=0
(
b
)
对
∀
x
∈
U
(
x
0
,
δ
0
)
,
F
(
x
0
,
f
(
x
0
))
=
0
(
c
)
若
F
(
x
⃗
,
y
)
在
U
(
x
⃗
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内存在关于各
x
i
的连续偏导数,那么
y
=
f
(
x
⃗
)
存在关于各
x
i
的连续偏导数,且
∂
f
(
x
⃗
)
∂
x
i
=
−
F
x
i
F
y
(
i
=
1
,
2
,
…
,
n
)
。
(c)若F(\vec{x},y)在U(\vec{x}_0,\delta)\times U(y_0,\delta)\ (\delta >0)内存在关于各x_i的连续偏导数,那么y=f(\vec{x})存在关于各x_i的连续偏导数,且\frac{\partial f(\vec{x})}{\partial x_i}=-\frac{F_{x_i}}{F_y}\ (i=1,2,\dots,n)。
(
c
)
若
F
(
x
,
y
)
在
U
(
x
0
,
δ
)
×
U
(
y
0
,
δ
)
(
δ
>
0
)
内存在关于各
x
i
的连续偏导数,那么
y
=
f
(
x
)
存在关于各
x
i
的连续偏导数,且
∂
x
i
∂
f
(
x
)
=
−
F
y
F
x
i
(
i
=
1
,
2
,
…
,
n
)
。
(隐函数组存在定理)
设向量函数
F
⃗
(
x
⃗
,
u
⃗
)
=
(
F
1
(
x
⃗
,
u
⃗
)
,
F
2
(
x
⃗
,
u
⃗
)
,
…
,
F
m
(
x
⃗
,
u
⃗
)
)
,
其中
x
⃗
=
(
x
1
,
x
2
,
…
,
x
n
)
∈
R
n
,
u
⃗
=
(
u
1
,
u
2
,
…
,
u
m
)
∈
R
m
,
在
U
(
x
⃗
0
,
δ
)
×
U
(
u
⃗
0
,
δ
)
(
δ
>
0
)
内满足条件:
设向量函数\vec{F}(\vec{x},\vec{u})=(F_1(\vec{x},\vec{u}),F_2(\vec{x},\vec{u}),\dots,F_m(\vec{x},\vec{u})),其中\vec{x}=(x_1,x_2,\dots,x_n)\in R^n,\vec{u}=(u_1,u_2,\dots,u_m)\in R^m,在U(\vec{x}_0,\delta)\times U(\vec{u}_0,\delta)\ (\delta>0)内满足条件:
设向量函数
F
(
x
,
u
)
=
(
F
1
(
x
,
u
)
,
F
2
(
x
,
u
)
,
…
,
F
m
(
x
,
u
))
,
其中
x
=
(
x
1
,
x
2
,
…
,
x
n
)
∈
R
n
,
u
=
(
u
1
,
u
2
,
…
,
u
m
)
∈
R
m
,
在
U
(
x
0
,
δ
)
×
U
(
u
0
,
δ
)
(
δ
>
0
)
内满足条件:
(
1
)
F
i
(
x
⃗
0
,
u
⃗
0
)
=
0
,
i
=
1
,
2
,
…
,
m
;
(1)F_i(\vec{x}_0,\vec{u}_0)=0,i=1,2,\dots,m;
(
1
)
F
i
(
x
0
,
u
0
)
=
0
,
i
=
1
,
2
,
…
,
m
;
(
2
)
F
i
(
x
⃗
,
u
⃗
)
与其关于
u
i
各个偏导在
U
(
x
⃗
0
,
δ
)
×
U
(
u
⃗
0
,
δ
)
内连续;
(2)F_i(\vec{x},\vec{u})与其关于u_i各个偏导在U(\vec{x}_0,\delta)\times U(\vec{u}_0,\delta)内连续;
(
2
)
F
i
(
x
,
u
)
与其关于
u
i
各个偏导在
U
(
x
0
,
δ
)
×
U
(
u
0
,
δ
)
内连续;
(
3
)
雅可比行列式
∂
(
F
1
,
F
2
,
…
,
F
m
)
∂
(
u
1
,
u
2
,
…
,
u
m
)
∣
x
⃗
=
x
⃗
0
;
u
⃗
=
u
⃗
0
≠
0
(3)雅可比行列式\frac{\partial (F_1,F_2,\dots,F_m)}{\partial (u_1,u_2,\dots,u_m)}|_{\vec{x}=\vec{x}_0;\vec{u}=\vec{u}_0}\ne0
(
3
)
雅可比行列式
∂
(
u
1
,
u
2
,
…
,
u
m
)
∂
(
F
1
,
F
2
,
…
,
F
m
)
∣
x
=
x
0
;
u
=
u
0
=
0
则
∃
δ
0
∈
(
0
,
δ
)
使得在
U
(
x
⃗
0
,
δ
0
)
×
U
(
u
⃗
0
,
δ
0
)
内唯一存在
m
维
n
元向量函数
则 \exists \ \delta_0 \in(0,\delta)使得在U(\vec{x}_0,\delta_0)\times U(\vec{u}_0,\delta_0)内唯一存在m维n元向量函数
则
∃
δ
0
∈
(
0
,
δ
)
使得在
U
(
x
0
,
δ
0
)
×
U
(
u
0
,
δ
0
)
内唯一存在
m
维
n
元向量函数
u
⃗
(
x
⃗
)
=
(
u
1
(
x
⃗
)
,
u
2
(
x
⃗
)
,
…
,
u
m
(
x
⃗
)
)
\vec{u}(\vec{x})=(u_1(\vec{x}),u_2(\vec{x}),\dots,u_m(\vec{x}))
u
(
x
)
=
(
u
1
(
x
)
,
u
2
(
x
)
,
…
,
u
m
(
x
))
满足:
(
a
)
u
⃗
0
=
(
u
1
(
x
⃗
0
)
,
u
2
(
x
⃗
0
)
,
…
,
u
m
(
x
⃗
0
)
)
;
(a)\vec{u}_0=(u_1(\vec{x}_0),u_2(\vec{x}_0),\dots,u_m(\vec{x}_0));
(
a
)
u
0
=
(
u
1
(
x
0
)
,
u
2
(
x
0
)
,
…
,
u
m
(
x
0
))
;
(
b
)
对任意
F
i
与
x
⃗
∈
U
(
x
⃗
0
,
δ
0
)
均有
F
i
(
x
⃗
,
u
⃗
(
x
⃗
)
)
=
0
;
(b)对任意F_i与\vec{x}\in U(\vec{x}_0,\delta_0)均有F_i(\vec{x},\vec{u}(\vec{x}))=0;
(
b
)
对任意
F
i
与
x
∈
U
(
x
0
,
δ
0
)
均有
F
i
(
x
,
u
(
x
))
=
0
;
(
c
)
若
F
i
对任意
x
j
有连续的偏导数,则
u
k
对
x
j
的偏导连续,记
(c)若F_i对任意x_j有连续的偏导数,则u_k对x_j的偏导连续,记
(
c
)
若
F
i
对任意
x
j
有连续的偏导数,则
u
k
对
x
j
的偏导连续,记
A
=
[
∂
F
1
(
x
⃗
,
u
⃗
)
∂
x
1
∂
F
1
(
x
⃗
,
u
⃗
)
∂
x
2
…
∂
F
1
(
x
⃗
,
u
⃗
)
∂
x
n
∂
F
2
(
x
⃗
,
u
⃗
)
∂
x
1
∂
F
2
(
x
⃗
,
u
⃗
)
∂
x
2
…
∂
F
2
(
x
⃗
,
u
⃗
)
∂
x
n
⋮
⋮
⋮
∂
F
m
(
x
⃗
,
u
⃗
)
∂
x
1
∂
F
m
(
x
⃗
,
u
⃗
)
∂
x
2
…
∂
F
m
(
x
⃗
,
u
⃗
)
∂
x
n
]
m
×
n
B
=
[
∂
F
1
(
x
⃗
,
u
⃗
)
∂
u
1
∂
F
1
(
x
⃗
,
u
⃗
)
∂
u
2
…
∂
F
1
(
x
⃗
,
u
⃗
)
∂
u
m
∂
F
2
(
x
⃗
,
u
⃗
)
∂
u
1
∂
F
2
(
x
⃗
,
u
⃗
)
∂
u
2
…
∂
F
2
(
x
⃗
,
u
⃗
)
∂
u
m
⋮
⋮
⋮
∂
F
m
(
x
⃗
,
u
⃗
)
∂
u
1
∂
F
m
(
x
⃗
,
u
⃗
)
∂
u
2
…
∂
F
m
(
x
⃗
,
u
⃗
)
∂
u
m
]
m
×
m
A=\begin{bmatrix} \frac{\partial F_1(\vec{x},\vec{u})}{\partial x_1}&\frac{\partial F_1(\vec{x},\vec{u})}{\partial x_2}&\dots&\frac{\partial F_1(\vec{x},\vec{u})}{\partial x_n}\\ \frac{\partial F_2(\vec{x},\vec{u})}{\partial x_1}&\frac{\partial F_2(\vec{x},\vec{u})}{\partial x_2}&\dots&\frac{\partial F_2(\vec{x},\vec{u})}{\partial x_n}\\ \vdots&\vdots&&\vdots\\ \frac{\partial F_m(\vec{x},\vec{u})}{\partial x_1}&\frac{\partial F_m(\vec{x},\vec{u})}{\partial x_2}&\dots&\frac{\partial F_m(\vec{x},\vec{u})}{\partial x_n} \end{bmatrix}_{m\times n} B=\begin{bmatrix} \frac{\partial F_1(\vec{x},\vec{u})}{\partial u_1}&\frac{\partial F_1(\vec{x},\vec{u})}{\partial u_2}&\dots&\frac{\partial F_1(\vec{x},\vec{u})}{\partial u_m}\\ \frac{\partial F_2(\vec{x},\vec{u})}{\partial u_1}&\frac{\partial F_2(\vec{x},\vec{u})}{\partial u_2}&\dots&\frac{\partial F_2(\vec{x},\vec{u})}{\partial u_m}\\ \vdots&\vdots&&\vdots\\ \frac{\partial F_m(\vec{x},\vec{u})}{\partial u_1}&\frac{\partial F_m(\vec{x},\vec{u})}{\partial u_2}&\dots&\frac{\partial F_m(\vec{x},\vec{u})}{\partial u_m}\\ \end{bmatrix}_{m\times m}
A
=
⎣
⎡
∂
x
1
∂
F
1
(
x
,
u
)
∂
x
1
∂
F
2
(
x
,
u
)
⋮
∂
x
1
∂
F
m
(
x
,
u
)
∂
x
2
∂
F
1
(
x
,
u
)
∂
x
2
∂
F
2
(
x
,
u
)
⋮
∂
x
2
∂
F
m
(
x
,
u
)
…
…
…
∂
x
n
∂
F
1
(
x
,
u
)
∂
x
n
∂
F
2
(
x
,
u
)
⋮
∂
x
n
∂
F
m
(
x
,
u
)
⎦
⎤
m
×
n
B
=
⎣
⎡
∂
u
1
∂
F
1
(
x
,
u
)
∂
u
1
∂
F
2
(
x
,
u
)
⋮
∂
u
1
∂
F
m
(
x
,
u
)
∂
u
2
∂
F
1
(
x
,
u
)
∂
u
2
∂
F
2
(
x
,
u
)
⋮
∂
u
2
∂
F
m
(
x
,
u
)
…
…
…
∂
u
m
∂
F
1
(
x
,
u
)
∂
u
m
∂
F
2
(
x
,
u
)
⋮
∂
u
m
∂
F
m
(
x
,
u
)
⎦
⎤
m
×
m
则
u
⃗
′
(
x
⃗
)
=
[
∂
u
1
(
x
⃗
)
∂
x
1
∂
u
1
(
x
⃗
)
∂
x
2
…
∂
u
1
(
x
⃗
)
∂
x
n
∂
u
2
(
x
⃗
)
∂
x
1
∂
u
2
(
x
⃗
)
∂
x
2
…
∂
u
2
(
x
⃗
)
∂
x
n
⋮
⋮
⋮
∂
u
m
(
x
⃗
)
∂
x
1
∂
u
m
(
x
⃗
)
∂
x
2
…
∂
u
m
(
x
⃗
)
∂
x
n
]
m
×
n
=
−
B
−
1
A
\vec{u}'(\vec{x})= \begin{bmatrix} \frac{\partial u_1(\vec{x})}{\partial x_1}&\frac{\partial u_1(\vec{x})}{\partial x_2}&\dots&\frac{\partial u_1(\vec{x})}{\partial x_n}\\ \frac{\partial u_2(\vec{x})}{\partial x_1}&\frac{\partial u_2(\vec{x})}{\partial x_2}&\dots&\frac{\partial u_2(\vec{x})}{\partial x_n}\\ \vdots&\vdots&&\vdots\\ \frac{\partial u_m(\vec{x})}{\partial x_1}&\frac{\partial u_m(\vec{x})}{\partial x_2}&\dots&\frac{\partial u_m(\vec{x})}{\partial x_n}\\ \end{bmatrix}_{m\times n}=-B^{-1}A
u
′
(
x
)
=
⎣
⎡
∂
x
1
∂
u
1
(
x
)
∂
x
1
∂
u
2
(
x
)
⋮
∂
x
1
∂
u
m
(
x
)
∂
x
2
∂
u
1
(
x
)
∂
x
2
∂
u
2
(
x
)
⋮
∂
x
2
∂
u
m
(
x
)
…
…
…
∂
x
n
∂
u
1
(
x
)
∂
x
n
∂
u
2
(
x
)
⋮
∂
x
n
∂
u
m
(
x
)
⎦
⎤
m
×
n
=
−
B
−
1
A
证明:(数学归纳法)
当
m
=
2
m=2
m
=
2
时,由于
∂
(
F
1
,
F
2
)
∂
(
u
1
,
u
2
)
∣
x
⃗
=
x
⃗
0
;
u
⃗
=
u
⃗
0
=
∣
∂
F
1
∂
u
1
∂
F
1
∂
u
2
∂
F
2
∂
u
1
∂
F
2
∂
u
2
∣
x
⃗
=
x
⃗
0
;
u
⃗
=
u
⃗
0
≠
0
\frac{\partial (F_1,F_2)}{\partial (u_1,u_2)}|_{\vec{x}=\vec{x}_0;\vec{u}=\vec{u}_0}=\begin{vmatrix}\frac{\partial F_1}{\partial u_1}&\frac{\partial F_1}{\partial u_2}\\\ \\\frac{\partial F_2}{\partial u_1}&\frac{\partial F_2}{\partial u_2}\end{vmatrix}_{\vec{x}=\vec{x}_0;\vec{u}=\vec{u}_0}\ne0
∂
(
u
1
,
u
2
)
∂
(
F
1
,
F
2
)
∣
x
=
x
0
;
u
=
u
0
=
∣
∣
∂
u
1
∂
F
1
∂
u
1
∂
F
2
∂
u
2
∂
F
1
∂
u
2
∂
F
2
∣
∣
x
=
x
0
;
u
=
u
0
=
0
则其中各行不可能所有元素为零,不妨假设
∂
F
2
∂
u
2
≠
0
\frac{\partial F_2}{\partial u_2}\ne 0
∂
u
2
∂
F
2
=
0
。若
∂
F
2
∂
u
2
=
0
\frac{\partial F_2}{\partial u_2}=0
∂
u
2
∂
F
2
=
0
,则
∂
F
2
∂
u
1
\frac{\partial F_2}{\partial u_1}
∂
u
1
∂
F
2
必不为零,同样可进行如下相同的处理:
由隐函数存在定理-2:
∃
δ
1
∈
(
0
,
δ
)
\exists \delta_1\in(0,\delta)
∃
δ
1
∈
(
0
,
δ
)
使得方程
F
2
(
x
⃗
,
u
1
,
u
2
)
=
0
F_2(\vec{x},{u}_1,u_2)=0
F
2
(
x
,
u
1
,
u
2
)
=
0
在
U
(
x
⃗
0
,
δ
1
)
×
U
(
u
1
0
,
δ
1
)
U(\vec{x}_0,\delta_1)\times U({u_1}^0,\delta_1)
U
(
x
0
,
δ
1
)
×
U
(
u
1
0
,
δ
1
)
内存在唯一的连续函数(其关于
u
1
u_1
u
1
偏导也连续)
u
2
=
u
2
(
x
⃗
,
u
1
)
,
且
∂
u
2
∂
u
1
=
−
∂
F
2
∂
u
1
∂
F
2
∂
u
2
u_2=u_2(\vec{x},u_1),且\frac{\partial u_2}{\partial u_1}=-\frac{\frac{\partial F_2}{\partial u_1}}{\frac{\partial F_2}{\partial u_2}}
u
2
=
u
2
(
x
,
u
1
)
,
且
∂
u
1
∂
u
2
=
−
∂
u
2
∂
F
2
∂
u
1
∂
F
2
代入另一方程得:
H
(
x
⃗
,
u
1
)
=
F
1
(
x
⃗
,
u
1
,
u
2
(
x
⃗
,
u
1
)
)
=
0
H(\vec{x},u_1) =F_1(\vec{x},u_1,u_2(\vec{x},u_1))=0
H
(
x
,
u
1
)
=
F
1
(
x
,
u
1
,
u
2
(
x
,
u
1
))
=
0
由于
∂
H
(
x
⃗
0
,
u
1
0
)
∂
u
1
=
∂
F
1
∂
u
1
+
∂
F
1
∂
u
2
∂
u
2
∂
u
1
=
∂
F
1
∂
u
1
−
∂
F
1
∂
u
2
∂
F
2
∂
u
1
∂
F
2
∂
u
2
=
1
∂
F
2
∂
u
2
(
∂
F
2
∂
u
2
∂
F
1
∂
u
1
−
∂
F
1
∂
u
2
∂
F
2
∂
u
1
)
=
1
∂
F
2
∂
u
2
∂
(
F
1
,
F
2
)
∂
(
u
1
,
u
2
)
≠
0
\frac{\partial H(\vec{x}_0,{u_1}^0)}{\partial u_1} =\frac{\partial {F_1}}{\partial u_1}+\frac{\partial F_1}{\partial u_2}\frac{\partial u_2}{\partial u_1}=\frac{\partial {F_1}}{\partial u_1}-\frac{\partial F_1}{\partial u_2}\frac{\frac{\partial F_2}{\partial u_1}}{\frac{\partial F_2}{\partial u_2}} =\frac{1}{\frac{\partial F_2}{\partial u_2}}(\frac{\partial F_2}{\partial u_2}\frac{\partial F_1}{\partial u_1}-\frac{\partial F_1}{\partial u_2}\frac{\partial F_2}{\partial u_1}) =\frac{1}{\frac{\partial F_2}{\partial u_2}}\frac{\partial (F_1,F_2)}{\partial (u_1,u_2)} \ne 0
∂
u
1
∂
H
(
x
0
,
u
1
0
)
=
∂
u
1
∂
F
1
+
∂
u
2
∂
F
1
∂
u
1
∂
u
2
=
∂
u
1
∂
F
1
−
∂
u
2
∂
F
1
∂
u
2
∂
F
2
∂
u
1
∂
F
2
=
∂
u
2
∂
F
2
1
(
∂
u
2
∂
F
2
∂
u
1
∂
F
1
−
∂
u
2
∂
F
1
∂
u
1
∂
F
2
)
=
∂
u
2
∂
F
2
1
∂
(
u
1
,
u
2
)
∂
(
F
1
,
F
2
)
=
0
则
∃
δ
0
∈
(
0
,
δ
1
)
\exists \delta_0\in(0,\delta_1)
∃
δ
0
∈
(
0
,
δ
1
)
使得方程
H
(
x
⃗
,
u
1
)
=
0
H(\vec{x},{u}_1)=0
H
(
x
,
u
1
)
=
0
在
U
(
x
⃗
0
,
δ
0
)
U(\vec{x}_0,\delta_0)
U
(
x
0
,
δ
0
)
内存在唯一连续函数
u
1
=
u
1
(
x
⃗
)
u_1=u_1(\vec{x})
u
1
=
u
1
(
x
)
故该方程组
{
F
1
(
x
⃗
,
u
1
,
u
2
)
=
0
F
2
(
x
⃗
,
u
1
,
u
2
)
=
0
确定了连续的隐函数组
{
u
1
=
u
1
(
x
⃗
)
u
2
=
u
2
(
x
⃗
,
u
1
(
x
⃗
)
)
\begin{cases}F_1(\vec{x},u_1,u_2)=0\\F_2(\vec{x},u_1,u_2)=0\end{cases}确定了连续的隐函数组\begin{cases}u_1=u_1(\vec{x})\\u_2=u_2(\vec{x},u_1(\vec{x}))\end{cases}
{
F
1
(
x
,
u
1
,
u
2
)
=
0
F
2
(
x
,
u
1
,
u
2
)
=
0
确定了连续的隐函数组
{
u
1
=
u
1
(
x
)
u
2
=
u
2
(
x
,
u
1
(
x
))
进一步,若
F
i
(
x
⃗
,
u
⃗
)
(
i
=
1
,
2
,
.
.
.
,
m
)
F_i(\vec{x},\vec{u})(i=1,2,…,m)
F
i
(
x
,
u
)
(
i
=
1
,
2
,
…
,
m
)
对
x
j
(
j
=
1
,
2
,
…
,
n
)
x_j(j=1,2,\dots,n)
x
j
(
j
=
1
,
2
,
…
,
n
)
均有连续偏导数
{
∂
F
1
∂
x
i
+
∂
F
1
∂
u
1
∂
u
1
∂
x
i
+
∂
F
1
∂
u
2
∂
u
2
∂
x
i
=
0
∂
F
2
∂
x
i
+
∂
F
2
∂
u
1
∂
u
1
∂
x
i
+
∂
F
2
∂
u
2
∂
u
2
∂
x
i
=
0
⟺
[
∂
F
1
∂
u
1
∂
F
1
∂
u
2
∂
F
2
∂
u
1
∂
F
2
∂
u
2
]
[
∂
u
1
∂
x
i
∂
u
2
∂
x
i
]
=
−
[
∂
F
1
∂
x
i
∂
F
2
∂
x
i
]
⟺
[
∂
F
1
∂
u
1
∂
F
1
∂
u
2
∂
F
2
∂
u
1
∂
F
2
∂
u
2
]
[
∂
u
1
∂
x
1
∂
u
1
∂
x
2
…
∂
u
1
∂
x
n
∂
u
2
∂
x
1
∂
u
2
∂
x
2
…
∂
u
2
∂
x
n
]
=
−
[
∂
F
1
∂
x
1
∂
F
1
∂
x
2
…
∂
F
1
∂
x
n
∂
F
2
∂
x
1
∂
F
2
∂
x
2
…
∂
F
2
∂
x
n
]
⟺
u
⃗
′
(
x
⃗
)
=
−
B
−
1
A
\begin{cases} \frac{\partial F_1}{\partial x_i}+\frac{\partial F_1}{\partial u_1}\frac{\partial u_1}{\partial x_i}+\frac{\partial F_1}{\partial u_2}\frac{\partial u_2}{\partial x_i}=0\\ \\ \frac{\partial F_2}{\partial x_i}+\frac{\partial F_2}{\partial u_1}\frac{\partial u_1}{\partial x_i}+\frac{\partial F_2}{\partial u_2}\frac{\partial u_2}{\partial x_i}=0\end{cases} \Longleftrightarrow \begin{bmatrix} \frac{\partial F_1}{\partial u_1}&\frac{\partial F_1}{\partial u_2}\\ \\ \frac{\partial F_2}{\partial u_1}&\frac{\partial F_2}{\partial u_2} \end{bmatrix} \begin{bmatrix}\frac{\partial u_1}{\partial x_i}\\ \\ \frac{\partial u_2}{\partial x_i} \end{bmatrix} =-\begin{bmatrix} \frac{\partial F_1}{\partial x_i}\\ \\ \frac{\partial F_2}{\partial x_i} \end{bmatrix} \Longleftrightarrow \begin{bmatrix} \frac{\partial F_1}{\partial u_1}&\frac{\partial F_1}{\partial u_2}\\ \\ \frac{\partial F_2}{\partial u_1}&\frac{\partial F_2}{\partial u_2} \end{bmatrix} \begin{bmatrix} \frac{\partial u_1}{\partial x_1}&\frac{\partial u_1}{\partial x_2}&\dots&\frac{\partial u_1}{\partial x_n}\\ \\ \frac{\partial u_2}{\partial x_1}&\frac{\partial u_2}{\partial x_2}&\dots&\frac{\partial u_2}{\partial x_n} \end{bmatrix} =-\begin{bmatrix} \frac{\partial F_1}{\partial x_1}&\frac{\partial F_1}{\partial x_2}&\dots&\frac{\partial F_1}{\partial x_n}\\ \\ \frac{\partial F_2}{\partial x_1}&\frac{\partial F_2}{\partial x_2}&\dots&\frac{\partial F_2}{\partial x_n} \end{bmatrix} \Longleftrightarrow \vec{u}'(\vec{x})=-B^{-1}A
⎩
⎨
⎧
∂
x
i
∂
F
1
+
∂
u
1
∂
F
1
∂
x
i
∂
u
1
+
∂
u
2
∂
F
1
∂
x
i
∂
u
2
=
0
∂
x
i
∂
F
2
+
∂
u
1
∂
F
2
∂
x
i
∂
u
1
+
∂
u
2
∂
F
2
∂
x
i
∂
u
2
=
0
⟺
⎣
⎡
∂
u
1
∂
F
1
∂
u
1
∂
F
2
∂
u
2
∂
F
1
∂
u
2
∂
F
2
⎦
⎤
⎣
⎡
∂
x
i
∂
u
1
∂
x
i
∂
u
2
⎦
⎤
=
−
⎣
⎡
∂
x
i
∂
F
1
∂
x
i
∂
F
2
⎦
⎤
⟺
⎣
⎡
∂
u
1
∂
F
1
∂
u
1
∂
F
2
∂
u
2
∂
F
1
∂
u
2
∂
F
2
⎦
⎤
⎣
⎡
∂
x
1
∂
u
1
∂
x
1
∂
u
2
∂
x
2
∂
u
1
∂
x
2
∂
u
2
…
…
∂
x
n
∂
u
1
∂
x
n
∂
u
2
⎦
⎤
=
−
⎣
⎡
∂
x
1
∂
F
1
∂
x
1
∂
F
2
∂
x
2
∂
F
1
∂
x
2
∂
F
2
…
…
∂
x
n
∂
F
1
∂
x
n
∂
F
2
⎦
⎤
⟺
u
′
(
x
)
=
−
B
−
1
A
假设对
m
−
1
m-1
m
−
1
个方程构成的方程组定理均成立,则
m
m
m
个方程构成的方程组经过一次消元后得到
m
−
1
m-1
m
−
1
个方程构成的方程组,可推知定理成立,此处不再赘述。