题目说明
- 给定一个数组 prices ,其中 prices[i] 表示股票第 i 天的价格。
- 在每一天,你可能会决定购买和/或出售股票。
- 你在任何时候最多只能持有一股股票。你也可以购买它,然后在同一天出售。
- 返回你能获得的最大利润 。
示例 1:
输入: prices = [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: prices = [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: prices = [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 3 * 10^4
0 <= prices[i] <= 10^4
解法
【基于Java】
//-----------------main------------------------
int[] prices = {7,1,4,3,2,6,4};
int maxValue = getMaxValue1(prices);
System.out.print("能获得的最大利润为:"+maxValue);
//-----------------method-1------------------------
private static int getMaxValue1(int[] prices) {
int value = 0;
int maxValue = 0;
// 排除异常情况
if (null == prices || prices.length < 2){
return 0;
}
for (int i = 0; i < prices.length; i++){
for (int j = i+1; j < prices.length; j++){
if (prices[j] > prices[i]){
// 只要是持续上涨,利润就一直累加【不考虑现实生活中的交易次数】
System.out.println("在第"+(i+1)+"天购入股票,在第"+(j+1)+"天卖出,这次能够获取的利润是:" + (prices[j] - prices[i]));
value = value + (prices[j] - prices[i]);
}
i = j;
}
if (value > maxValue){
maxValue = value;
}
}
return maxValue;
}
//-----------------method-2------【复杂度降低但执行速度稍慢】------------------
private static int getMaxValue2(int[] prices) {
int value = 0;
// 排除异常情况
if (null == prices || prices.length < 2){
return 0;
}
for (int i = 0; i < prices.length-1; i++){
if (prices[i+1] > prices[i]){
value = value + (prices[i+1] - prices[i]);
}
}
return value;
}
思路
-
贪心算法:在对问题求解时,总是做出在当前看来是最好的选择。即不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
-
局部最优解
-
脱离现实生活思维
-
多临界条件判定思维:可以是满足上升趋势的情况下就累加,或者一旦不满足上升趋势了就计算临界值。
例:第三天到第四天开始上涨,第三天为临界最低值,第六天到第七天开始下跌,第六天为临界最高值; 1. 可以直接计算第三天到第六天的上涨跨度值; 2. 也可以将3-4,4-5,5-6三个区间段的上涨值累计相加。 结果一样,只是在代码实现和逻辑思维上稍有区别。
图解
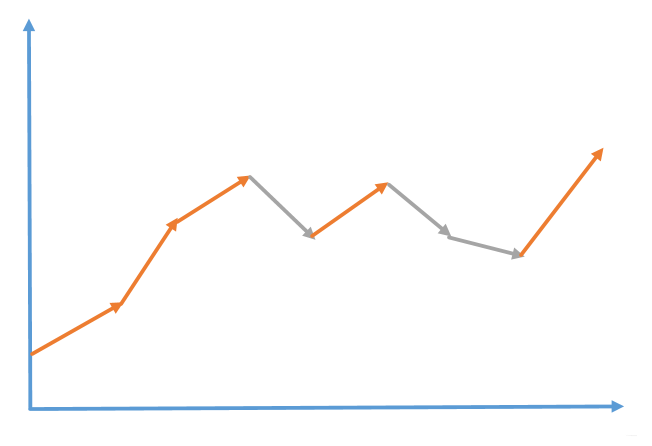
版权声明:本文为AZHOU_princeSS原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。