整本书的知识点,点击右方链接
:
整本书笔记知识点
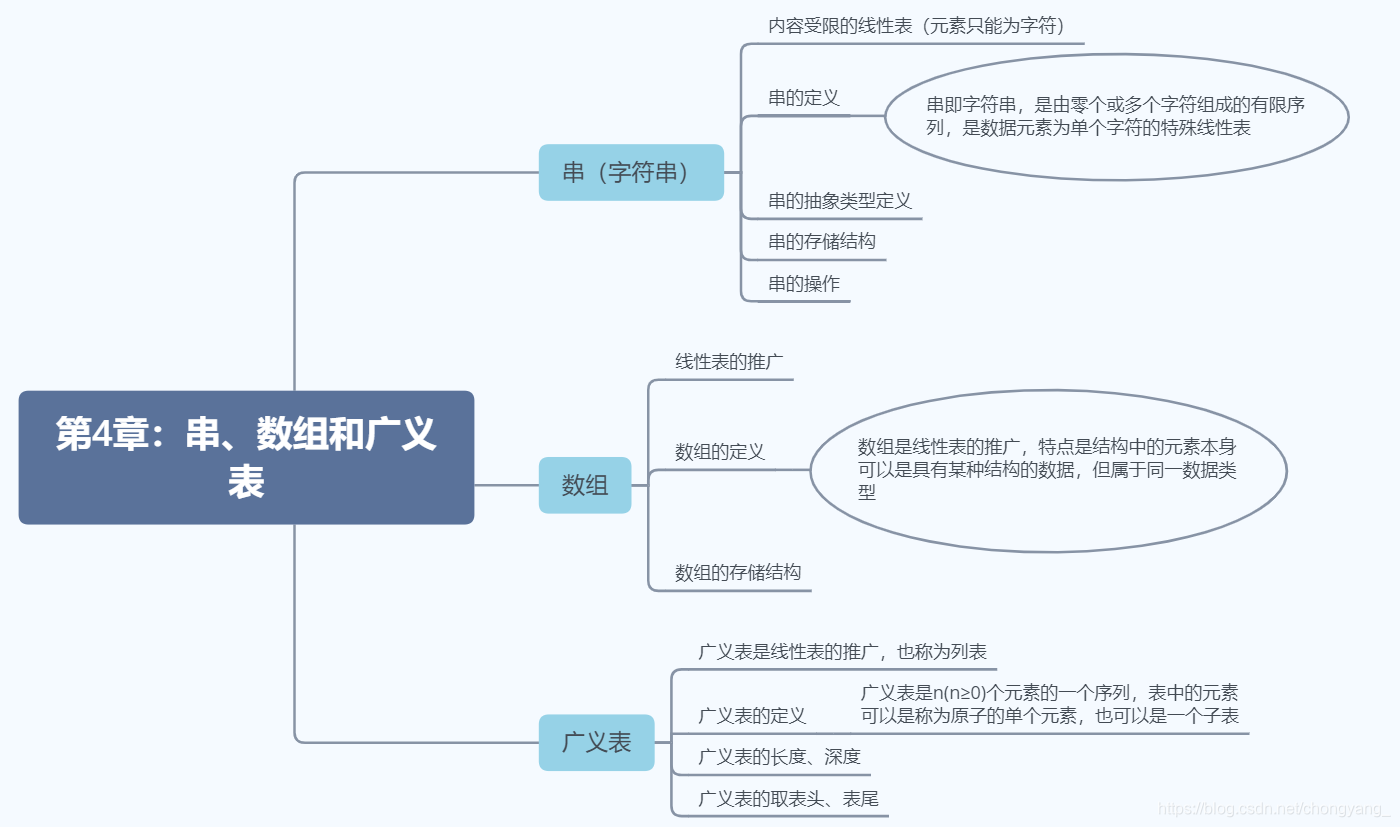
四、串、数组和广义表
4.1、串的定义
串即字符串,是由零个或多个字符组成的有限序列,是数据元素为单个字符的特殊线性表。
- 串是内容受限的线性表,它限定了表中的元素为字符
- 串长:串中字符个数(n≥0). n=0 时称为空串
- 空白串:由一个或多个空格符组成的串
- 子串:串S中任意个连续的字符序列叫S的子串; S叫主串
-
当两个串的长度相等,并且各个对应位置的字符都相等时,才称这两个串相等
4.2、案例引入
略
4.3、串的类型定义、存储结构及其运算
4.3.1、串的抽象类型定义
ADT Sting{
//数据对象
Objects: D = {ai | ai∈CharacterSet, i=1, 2, …,n, n≥0}
//数据关系
Relations: R1={ <ai - 1, ai > | ai - 1, ai ∈D, i = 2, …,n }
//基本操作
functions: // 有13种之多
StrAssign(&T, chars) // 串赋值,生成值为chars的串T
StrCompare(S, T) // 串比较,若S>T,返回值大于0…
StrLength(S) // 求串长,即返回S的元素个数
Concat(&T, S1, S2) // 串连接,用T返回S1+S2的新串
SubString(&Sub, S, pos, len) // 求S中pos起长度为len的子串
……
Index(S, T, pos) // 返回子串T在pos之后的位置
Replace(&S, T, V) // 用子串V替换子串T
}
ADT Sting
4.3.2、串的存储结构
①、
定长顺序存储
:用一组连续的存储单元来存放串,直接使用定长的字符数组来定义,数组的上界预先给出,故称为静态存储分配。
例如
C语言约定在串尾加结束符 ‘ \0’,以利操作加速,但不计入串长;
若字符串超过Maxstrlen 则自动截断(因为静态数组存不进去)
想存放超长字符串怎么办?——静态数组有缺陷。 改用动态分配的一维数组 堆
②、堆分配存储
:仍用一组连续的存储单元来存放串,但存储空间是在程序执行过程中动态按需分配而得
三、
链式存储
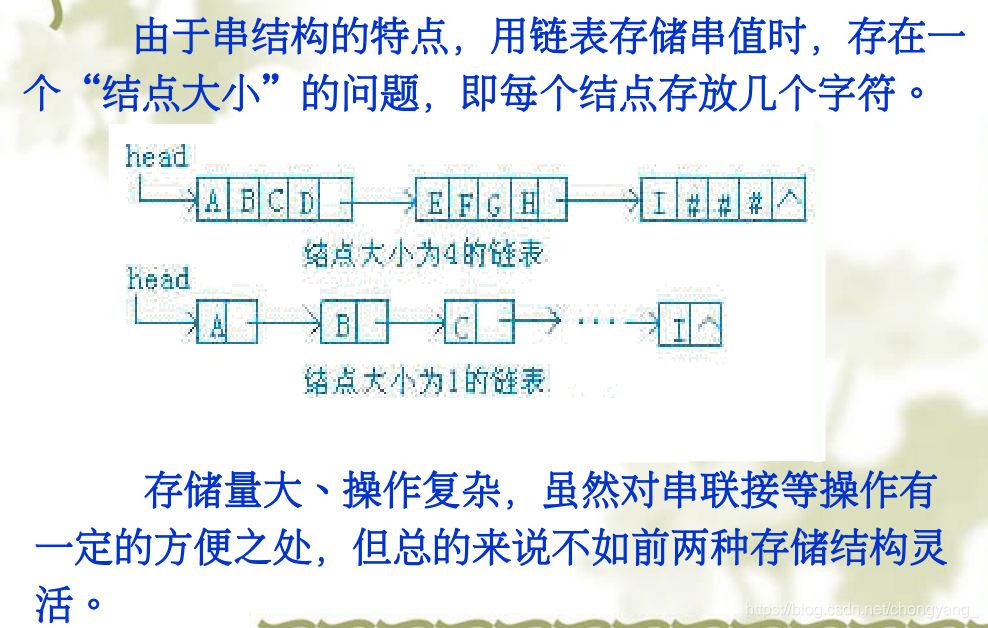
4.3.3、串的模式匹配算法
课时缩短,计划中不讲也不学这个。
想学的话跳转链接:
串的总结
4.4、数组
数组是线性表的推广,特点是结构中的元素本身可以是具有某种结构的数据,但属于同一数据类型
1.一维数组
一维数组可看成是一个线性表或一个向量,存储在一块连续的存储单元中,适合于随机查找。一维数组记为A[n]或A=(a0,al,…ai,…,an-1) ,一维数组中ai的存储地址LOC(ai)可由下式求出:
LOC(ai)=LOC(a0)+i*L (0≤i<n)
2.二维数组
二维数组,又称矩阵(matrix)。每个元素又是一个定长的线性表(一维数组),都要受到两个关系即行关系和列关系的约束,也就是每个元素都同属于两个线性表。例如,设A是一个有m行n列的二维数组,A可以看成由m个行向量组成的向量,也可以看由n个列向量组成的向量。
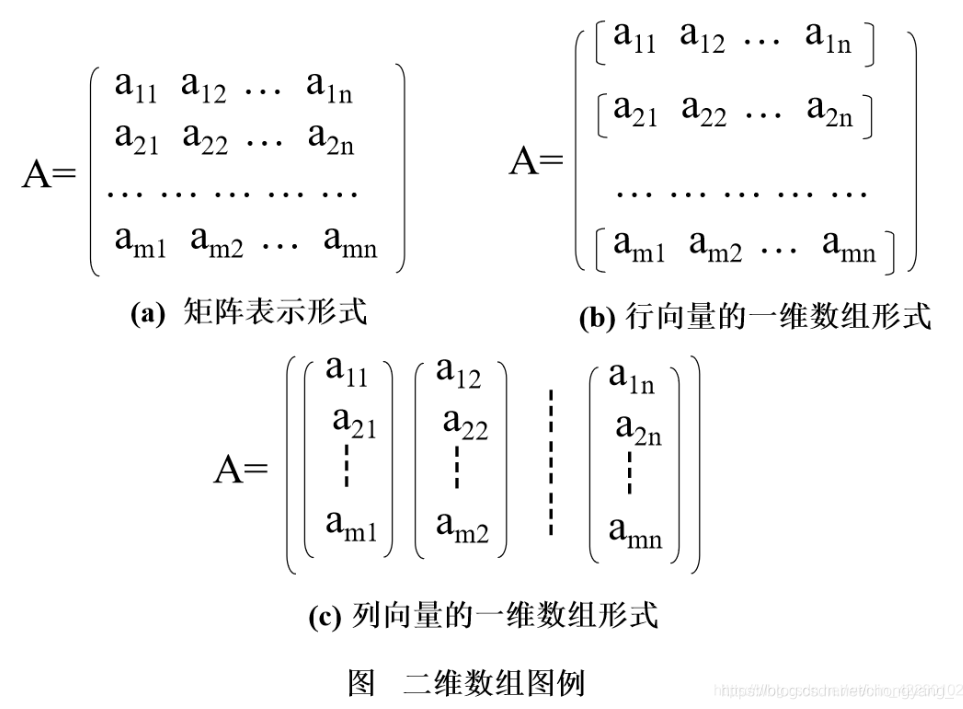
一个二维数组可以看作是每个数据元素类型相都同的一维数组。以此类推,任何多维数组都可以看作一个线性表,这时线性表中的每个数据元素也是一个线性表。多维数组是特殊的线性表,是线性表的推广。
链接:
数组和广义表详细知识点
4.5、广义表
广义表是线性表的推广,也称为列表。
广义表是n(n≥0)个元素的一个序列,表中的元素可以是称为原子的单个元素,也可以是一个子表
若n=0时则称为空表。设ai为广义表的第i个元素,则广义表的一般表示与线性表相同
LS=(a1,a2,…,ai,…,an)
其中n表示广义表的长度,n≥0。ai可以是单个元素,也可以是广义表
如果ai是单个数据元素,则ai是广义表LS的原子;如果ai是一个广义表,则ai是广义表LS的子表
习惯上,用大写字母表示广义表的名称,用小写字母表示原子
广义表的长度(广度)指:广义表中所包含的数据元素的个数
例如,在广义表 (a,(b,c,d)) 中,它包含一个原子和一个子表,因此该广义表的长度为 2。
再比如,广义表 ((a,b,c)) 中只有一个子表 (a,b,c),因此它的长度为 1。
广义表的深度,可以通过观察该表中所包含括号的层数间接得到。这里需要注意,数左括号(或右括号)时同一层次的多个括号只计算一次
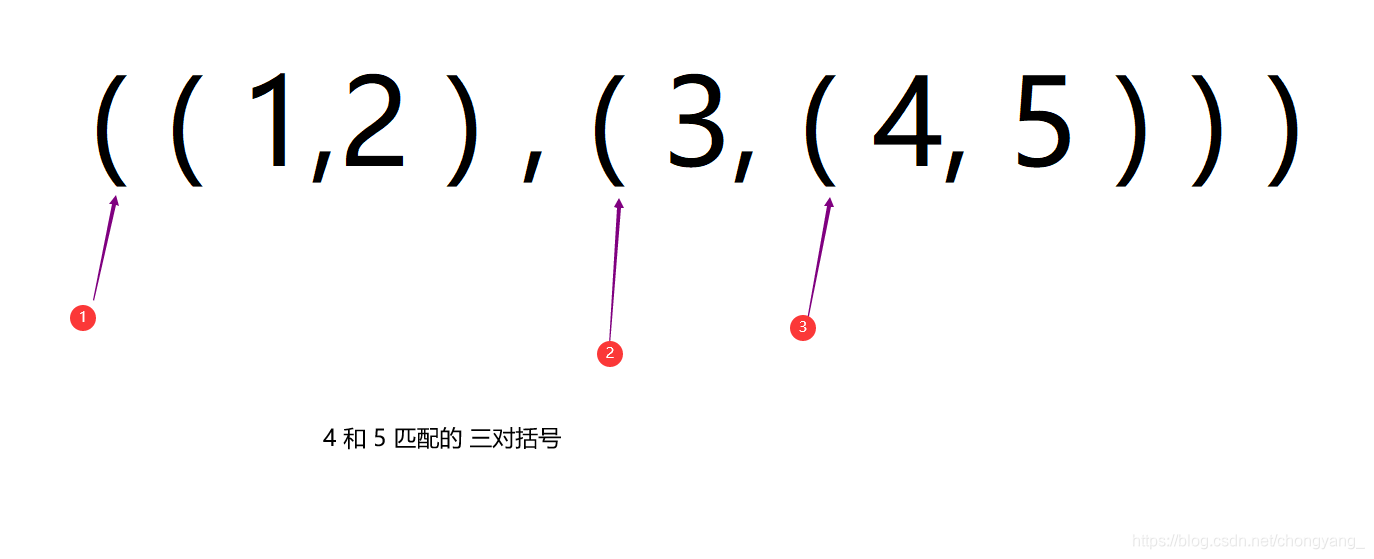
比如:广义表 ((1,2),(3,(4,5))) 中,此广义表中包含 3 层括号,因此深度为 3
广义表深度 = 匹配最多括号的元素所匹配的括号对数,如上例子中的 4 和 5 都匹配了 3 对括号。
题目1
:广义表 (a,(a,b),d,e,
((i,j),k)
) 的长度是( ),深度是( )
其长度为5、深度为3、
为什么呢
?
长度的求法为最大括号中的逗号数加1
即为:
a 后面的逗号,
(a,b) 后面的逗号,
d 后面的逗号,
e 后面的逗号,
((i,j),k)
前面的逗号,
总计有四个,那么广义表的长度是4+1=5;
深度的求法为上面每个元素的括号匹配数加1的最大值
a为0+1=1;
(a,b)为1+1=2;
d,e类似a;
==((i,j),k)==为2+1=3;
故深度为3。
原文:https://blog.csdn.net/w_k_l/article/details/78983957

广义表三个重要结论
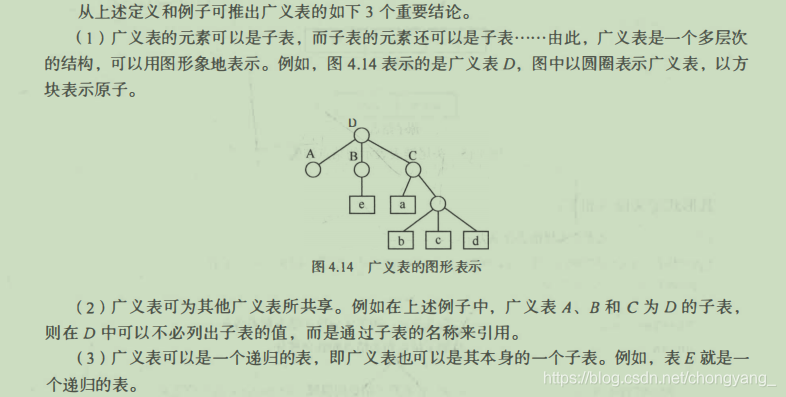
取表头GetHead(LS):取出表头为非空广义表的第一个元素,它可以是一个单原子,也可以是一个子表
取表尾GetTail(LS):取出的表尾为除去表头之外,由其余元素构成的表。即表尾一定是一个广义表

已知广义表: A=(a,b), B=(A,A), C=(a,(b,A),B), 求下列运算的结果:
tail(head(tail©)) =( )
head() 返回列表的第一个元素;
tail() 返回列表的删去第一个元素之后的剩余列表;
所以,
tail©=((b,A),B);
head(tail©)=head( ((b,A),B) )=(b,A)
tail (head(tail©) )=tail( (b,A) )=(A)
注意,head返回的是元素 (去掉最外层括号) 此元素可以是原子也可能是子表,tail返回的是表(保留最外层括号)。
广义表( )和 (( )) 不同。前者为空表,长度n = O; 后者长度 n = 1, 可分解得到其表头、 表尾均为空表()
第四章小结
- 串是内容受限的线性表,它限定了表中的元素为字符
- 多维数组可以看成是线性表的推广,其特点是结构中的元素本身可以是具有某种结构的数据,但属于用一数据类型
- 广义表是另一种线性表的推广形式,表中的元素可以是称为原子的单个元素,也可以是一个子表,所以线性表可以看成广义表的特例
第四章习题
(1)串是一种特殊的线性表,其特殊性体现在( )。
A.可以顺序存储 B.数据元素是一个字符
C.可以链式存储 D.数据元素可以是多个字符若
答案:B
串是内容受限的线性表,表中元素只能存字符
(2)串下面关于串的的叙述中,( )是不正确的?
A.串是字符的有限序列 B.空串是由空格构成的串
C.模式匹配是串的一种重要运算 D.串既可以采用顺序存储,也可以采用链式存储
答案:B
解释:空格常常是串的字符集合中的一个元素,有一个或多个空格组成的串成为空格串,零个字符的串成为空串,其长度为零。
(3)串“ababaaababaa”的next数组为( )。
A.012345678999 B.012121111212 C.011234223456 D.0123012322345
答案:C
(4)串“ababaabab”的nextval为( )。
A.010104101 B.010102101 C.010100011 D.010101011
答案:A
(5)串的长度是指( )。
A.串中所含不同字母的个数 B.串中所含字符的个数
C.串中所含不同字符的个数 D.串中所含非空格字符的个数
答案:B
解释:串中字符的数目称为串的长度。
(6)假设以行序为主序存储二维数组A=array[1…100,1…100],设每个数据元素占2个存储单元,基地址为10,则LOC[5,5]=( )。
A.808 B.818 C.1010 D.1020
答案:B
解释:以行序为主,则LOC[5,5]=[(5-1)*100+(5-1)]*2+10=818。
(7)设有数组A[i,j],数组的每个元素长度为3字节,i的值为1到8,j的值为1到10,数组从内存首地址BA开始顺序存放,当用以列为主存放时,元素A[5,8]的存储首地址为( )。
A.BA+141 B.BA+180 C.BA+222 D.BA+225
答案:B
解释:以列序为主,则LOC[5,8]=[(8-1)*8+(5-1)]*3+BA=BA+180。
(8)设有一个10阶的对称矩阵A,采用压缩存储方式,以行序为主存储,a11为第一元素,其存储地址为1,每个元素占一个地址空间,则a85的地址为( )
A.13 B.32 C.33 D.40
答案:C
(9)若对n阶对称矩阵A以行序为主序方式将其下三角形的元素(包括主对角线上所有元素)依次存放于一维数组B[1…(n(n+1))/2]中,则在B中确定aij(i<j)的位置k的关系为( )。
A.i*(i-1)/2+j B.j*(j-1)/2+i C.i*(i+1)/2+j D.j*(j+1)/2+i
答案:B
(10)二维数组A的每个元素是由10个字符组成的串,其行下标i=0,1,…,8,列下标j=1,2,…,10。若A按行先存储,元素A[8,5]的起始地址与当A按列先存储时的元素( )的起始地址相同。设每个字符占一个字节。
A.A[8,5] B.A[3,10] C. A[5,8] D.A[0,9]
答案:B
解释:设数组从内存首地址M开始顺序存放,若数组按行先存储,元素A[8,5]的起始地址为:M+[(8-0)*10+(5-1)]*1=M+84;若数组按列先存储,易计算出元素A[3,10]的起始地址为:M+[(10-1)*9+(3-0)]*1=M+84。故选B。
(11)设二维数组A[1… m,1… n](即m行n列)按行存储在数组B[1… m*n]中,则二维数组元素A[i,j]在一维数组B中的下标为( )。
A.(i-1)
n+j B.(i-1)
n+j-1 C.i
(j-1) D.j
m+i-1
答案:A
解释:特殊值法。取i=j=1,易知A[1,1]的的下标为1,四个选项中仅有A选项能确定的值为1,故选A。
(12)数组A[0…4,-1…-3,5…7]中含有元素的个数( )。
A.55 B.45 C.36 D.16
答案:B
解释:共有5
3
3=45个元素。
(13)广义表A=(a,b,(c,d),(e,(f,g))),则Head(Tail(Head(Tail(Tail(A)))))的值为( )。
A.(g) B.(d) C.c D.d
答案:D
解释:Tail(A)=(b,(c,d),(e,(f,g)));Tail(Tail(A))=( (c,d),(e,(f,g))); Head(Tail(Tail(A)))= (c,d);Tail(Head(Tail(Tail(A))))=(d);Head(Tail(Head(Tail(Tail(A)))))=d。
(14)广义表((a,b,c,d))的表头是( ),表尾是( )。
A.a B.( ) C.(a,b,c,d) D.(b,c,d)
答案:C、B
解释:表头为非空广义表的第一个元素,可以是一个单原子,也可以是一个子表,((a,b,c,d))的表头为一个子表(a,b,c,d);表尾为除去表头之外,由其余元素构成的表,表为一定是个广义表,((a,b,c,d))的表尾为空表( )。
(15)设广义表L=((a,b,c)),则L的长度和深度分别为( )。
A.1和1 B.1和3 C.1和2 D.2和3
答案:C
解释:广义表的深度是指广义表中展开后所含括号的层数,广义表的长度是指广义表中所含元素的个数。根据定义易知L的长度为1,深度为2