DBSCAN(Density-Based Spatial Clustering of Applications with Noise)

K-Means是最常见的聚类方法，能够实现快速聚类，但局限于其算法构架，

K-Means对非球形边界的数据很难达到一个较好的分类效果，因此我们需要借助另外的数学理理论工具对其进行进一步的完善。

这里介绍一种利用密度进行聚类的方法：DBSCAN。一方面作为聚类算法的补充内容，一方面需要掌握面一个新算法如何利用scikit-learn快速上手应用实践的方法，当然最重要的一点，是要树立关于密度的基本认知，为后续学习核函数做铺垫。

基本原理

DBSCAN是一种基于密度的聚类方法，旨在寻找被低密度区域分离的高密度区域。

DBSCAN是一种简单、有效的基于密度的聚类算法，且包含了基于密度的许多方法中的重要概念。尽管定义密度的方法没有定义相似度的方法多，但仍存在几种不同的方法，本部分中，我们讨论DBSCAN使用的基于中心的定义是否相似的方法。

在基于中心的方法中，数据集中特定点的密度通过对该点Eps半径之内的点计数（包括点本身）来估计，如下图所示。点A的Eps半径内点的个数为7，包括A本身。该方法实现简单，但是点的密度取决于指定的半径。例如，如果半径足够大，则所有点的密度都等于数据集中的点数m。同理，如果半径太小，则所有点的密度都是1。对于低维数据，一种确定合适半径的方法在讨论DBSCAN算法时给出。



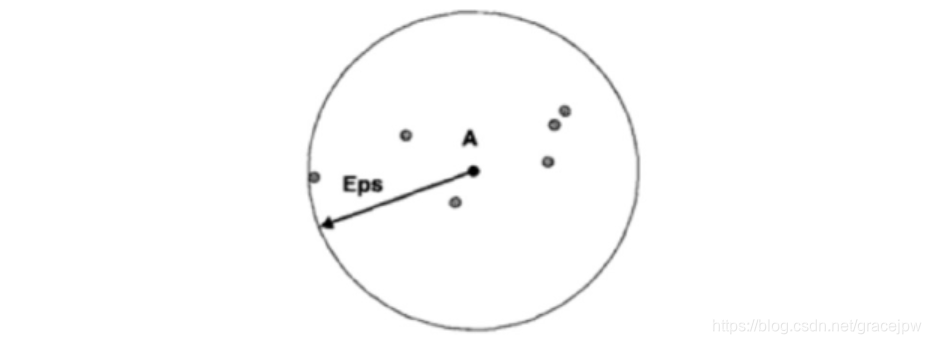
密度的基于中心的方法使得我们可以将点分类为（1）稠密区域内部的点（核心点），（2）稠密区域边缘上的点（边界点），（3）稀疏区域中的点（噪声或背景点）。下图使用二维点集图示了核心点、边界点和噪声点的概念。下文给出更详尽的描述。




核心点（core point）

：这些点在基于密度的簇内部。点的领域由距离函数和用户指定的距离参数Eps决定。核心点的定义是，如果该点的给定领域内的点的个数超过给定的阈值MinPts，其中MinPts也是一个用户指定的参数。在上图中，如果MinPts≤7，则对于给定的半径（Eps），点A是核心点。


边界点（border point）

：边界点不是核心点，但它落在某个核心点的领域内。在上图中，点B是边界点。边界点可能落在多个核心点的领域内。


噪声点（noise point）

：噪声点是既非核心点也非边界点的任何点。在上图中，点C是噪声点。

算法过程

给定核心点、边界点和噪声点的定义，DBSCAN算法可以非正式地描述如下。任意两个足够靠近（相互之间的距离在Eps之内）的核心点将放在同⼀一个簇中。同样，任何与核心点足够靠近的边界点也放到与核心点相同的簇中。（如果一个边界点靠近不同簇的核心点，则可能需要解决平局问题。）噪声点被丢弃。算法的细节在伪代码中给出。


聚类分析：DBSCAN算法

1. 将所有点标记为核心点、边界点或噪声点
2. 删除噪声点
3. 为距离在Eps之内的所有核心点之间赋予一条边
4. 每个彼此联通的核心点组成⼀一个簇
5. 将每个边界点指派到一个与之关联的核心点的簇当中

当然，还有如何确定参数Eps和MinPts的问题。基本方法是观察点到它的k个最近邻的距离（称为-距离）的特性。对于属于某个簇的点，如果k不大于簇的大小，则k-距离将很小。注意，尽管因簇的密度和点的随机分布不同而有变化，但是如果簇密度的差异不是很极端的话，在平均情况下变化不会太大。

然而，对于不在簇中的点（如噪声点），k-距离将相对较大。因此，如果我们对于某个k，计算所有点的k-距离，以递增次序将它们排序，然后绘制排序后的值，则会看到k-距离的急剧变化，对应于合适的Eps值。如果我们选取该距离为Eps参数，而取k的值为MinPts参数，则k-距离小于Eps的点将被标记为核心点，而其他点将被标记为噪声或边界点。

Scikit-Learn实现

接下来，利用Scikit-Learn快速实践DBSCAN算法。


生成数据集


为了更好地对比K-Means快速聚类和DBSCAN聚类，此处利用sklearn生成一个非线性边界的数据集。这里需要注意，sklearn提供了非常丰富的生成数据的方法，用以在无外部数据集的情况下测试模型性能，该功能主要由datasets 模块提供。此处利用该模块的make_moons方法生成非线性边界的数据集。

from sklearn.datasets import make_moons 
#一个简单的玩具数据集可视化聚类和分类算法。
X,y = make_moons(200, noise = 0.05, random_state=0)

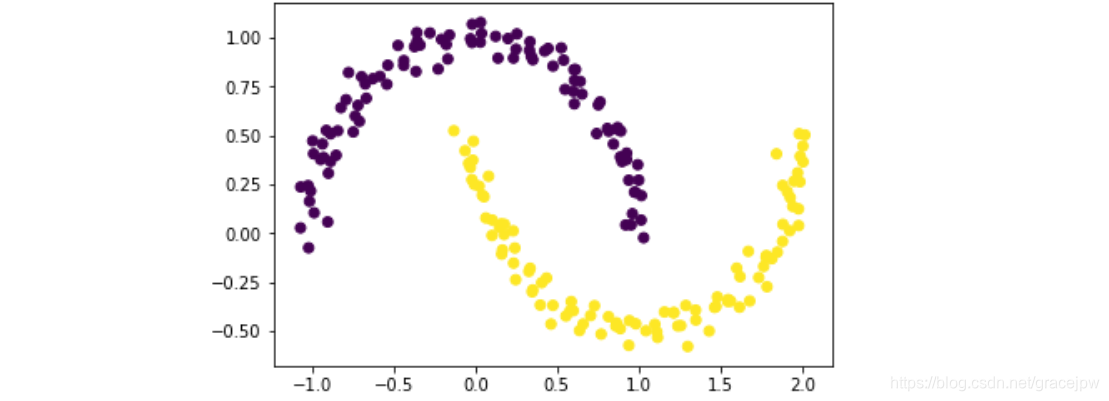
此时生成了一个二维数组数据集X，数据集形如弯月，且内部每个元素根据初始簇设置有对应的标签，该初始簇归属情况由原始质心划分方法决定。数据集基本情况如下所示：

plt.scatter(X[:,0],X[:,1], c=y)

K_Means聚类实验


该数据集用K_Means聚类很难捕捉到原始数据集的非线性边界下的自然结构。sklearn的聚类算法保存在cluster模块中，我们首先尝试使用K-Means对其进行聚类处理。

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)

注意，虽然K-Means是无监督学习，但在sklearn中该算法也作为评估器而存在，因此，使用方法也要遵照评估器的一般使用规则。在模型训练完成后，可使用模型的labels_ 属性查看各训练数据所属簇的划分情况，也可调用predict方法在对原始数据进行预测，从而生成各个点的所属簇标签。

labels = kmeans.labels_
labels

array([0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0,
       1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1,
       0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1,
       1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1,
       0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1,
       1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1,
       1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1,
       0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0,
       0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1,
       1, 0])

kmeans.predict(X)#kmeans.predict(X)== kmeans.labels_

array([0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0,
       1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1,
       0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1,
       1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1,
       0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1,
       1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1,
       1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1,
       0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0,
       0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 0, 1,
       1, 0])

同时模型cluster_centers_ 属性保存了聚类结果的中心点：

#模型cluster_centers_ 属性保存了聚类结果的中⼼点
centers = kmeans.cluster_centers_
centers

array([[ 1.20736718, -0.0825517 ],
       [-0.2003285 ,  0.58035606]])

#利用可视化图形查看最终聚类结果
plt.scatter(X[:,0],X[:,1], c = labels)
plt.plot(centers[:,0], centers[:,1],'ro')

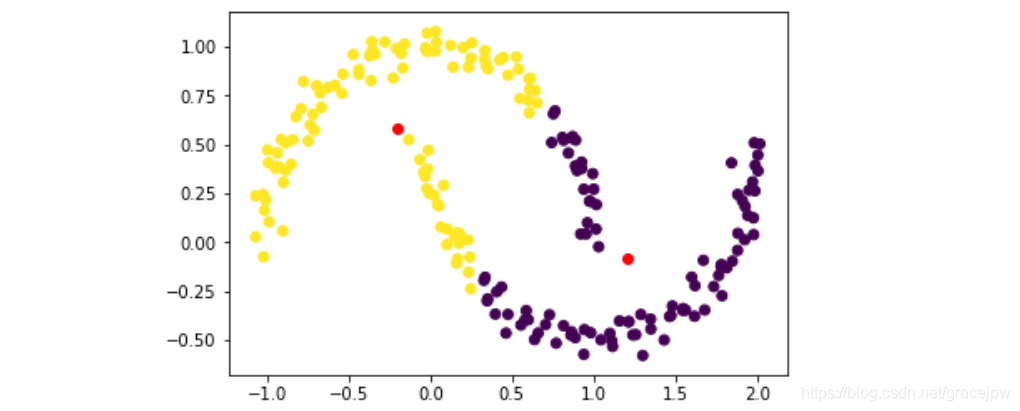
很明显K-Means并没有准确的捕捉数据集背后的客观分类规律，接下来尝试用DBSCAN进行聚类。


DBSCAN聚类实践


在调用sklearn中DBSCAN算法时，需要设置eps半径长度以及核心点的判别条件。

#DBSCAN聚类实践
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.3, min_samples=10)
db.fit(X)

DBSCAN(algorithm='auto', eps=0.3, leaf_size=30, metric='euclidean',
    metric_params=None, min_samples=10, n_jobs=None, p=None)

# 模型训练完成后，数据集各点所属类同样保存在db.labels_属性中
db.labels_

array([0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1,
       0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1,
       1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0,
       0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0,
       1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0,
       0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0,
       0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0,
       1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1,
       1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1,
       0, 1], dtype=int64)

然后利用图形可视化展示聚类结果：

plt.scatter(X[:,0],X[:,1], c = db.labels_)

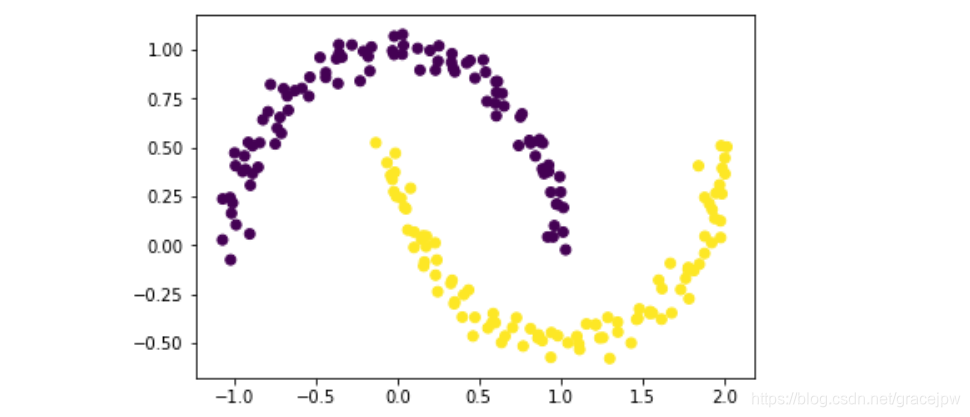
能够看出，DBSCAN成功捕捉数据集分类结构。