本文主要讲解PyTorch中的卷积函数Conv2d以及对应的空洞卷积Dilated
Conv2d
nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)
此函数作一个卷积操作,将输入为
(N
,
C
i
n
,
H
,
W
)
(N, ~C_{in}, ~H, ~W)
(
N
,
C
i
n
,
H
,
W
)
的输入变为
(N
,
C
o
u
t
,
H
o
u
t
,
W
o
u
t
)
(N, ~C_{out}, ~H_{out}, ~W_{out})
(
N
,
C
o
u
t
,
H
o
u
t
,
W
o
u
t
)
,其中
NN
N
是batch size,
CC
C
代表通道数,
H和
W
H和W
H
和
W
分别是图像的长和宽
输出的长和宽的计算
H
o
u
t
=
H
i
n
+
2
∗
p
a
d
d
i
n
g
[
0
]
−
d
i
l
a
t
i
o
n
[
0
]
∗
(
k
e
r
n
e
l
_
s
i
z
e
[
0
]
−
1
)
−
1
s
t
r
i
d
e
[
0
]
+
1
W
o
u
t
=
W
i
n
+
2
∗
p
a
d
d
i
n
g
[
1
]
−
d
i
l
a
t
i
o
n
[
1
]
∗
(
k
e
r
n
e
l
_
s
i
z
e
[
1
]
−
1
)
−
1
s
t
r
i
d
e
[
1
]
+
1
H_{out} = \frac{H_{in}+2*padding[0]-dilation[0]*(kernel\_size[0]-1)-1}{stride[0]}+1 \\ W_{out} = \frac{W_{in}+2*padding[1]-dilation[1]*(kernel\_size[1]-1)-1}{stride[1]}+1
H
o
u
t
=
s
t
r
i
d
e
[
0
]
H
i
n
+
2
∗
p
a
d
d
i
n
g
[
0
]
−
d
i
l
a
t
i
o
n
[
0
]
∗
(
k
e
r
n
e
l
_
s
i
z
e
[
0
]
−
1
)
−
1
+
1
W
o
u
t
=
s
t
r
i
d
e
[
1
]
W
i
n
+
2
∗
p
a
d
d
i
n
g
[
1
]
−
d
i
l
a
t
i
o
n
[
1
]
∗
(
k
e
r
n
e
l
_
s
i
z
e
[
1
]
−
1
)
−
1
+
1
参数的含义
-
in_channels
([
int
]) – 输入图像通道数 -
out_channels
([
int
])– 输出图像通道数(等于卷积核的数目) -
kernel_size
([
int
]
or
[
tuple
]) – 卷积核的大小 -
stride
([
int
]
or
[
tuple
]
,
optional
) – 卷积核移动的步长. Default: 1 -
padding
([
int
]
,
[
tuple
]
or
[
str
]
,
optional
) – 图像填充的数目. Default: 0 -
padding_mode
(
string
*,*
optional
) – 填充模式
'zeros'
,
'reflect'
,
'replicate'
or
'circular'
. Default:
'zeros'
-
dilation
([
int
]
or
[
tuple
]
,
optional
) – Spacing between kernel elements. Default: 1 -
groups
([
int
]
,
optional
) – Number of blocked connections from input channels to output channels. Default: 1 -
bias
([
bool
]
,
optional
) – If
True
, adds a learnable bias to the output. Default:
True
例子
''' padding=0,stride=1,kernel_size=3 '''
x = torch.randn(1,1,4,4)
l = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3)
y = l(x)
print(y.size()) # torch.Size([1, 1, 2, 2])
''' padding=2,stride=1,kernel_size=4 '''
x = torch.randn(1,1,5,5)
l = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=4, padding=2)
y = l(x)
print(y.size()) # torch.Size([1, 1, 6, 6])
下面图示了一个4*4图片,kernel size=4 stride=1 padding=0的卷积图示(只展示了一个卷积核)
注意:对于padding的图,仅仅变化的就是原图,其余的过程不变
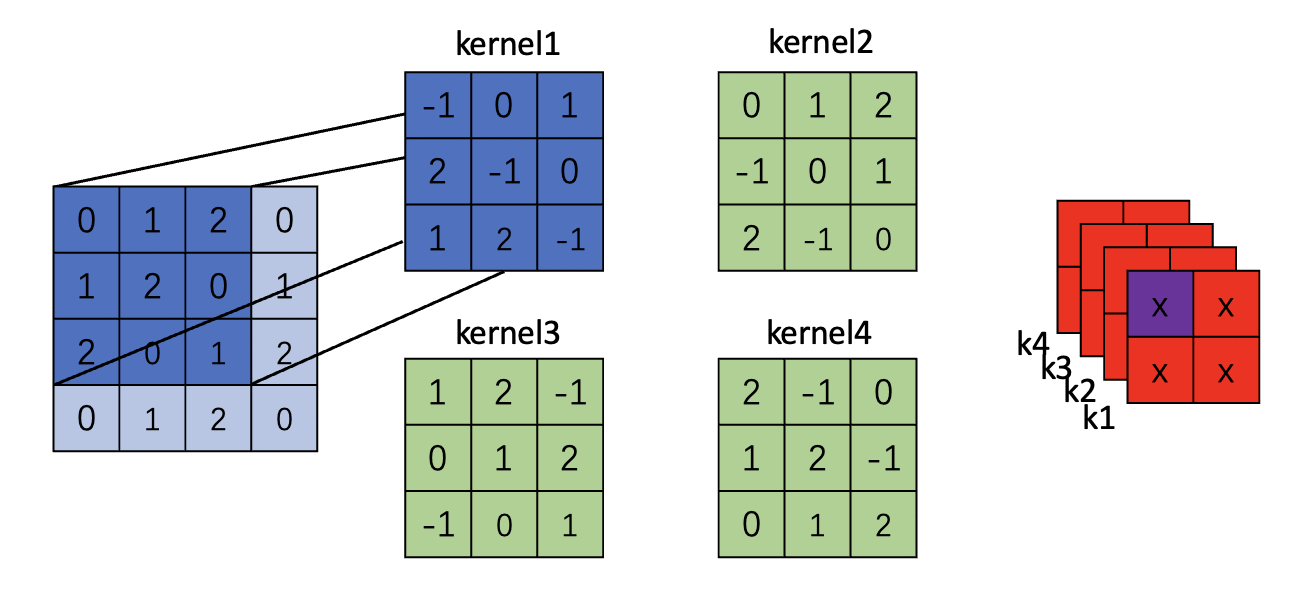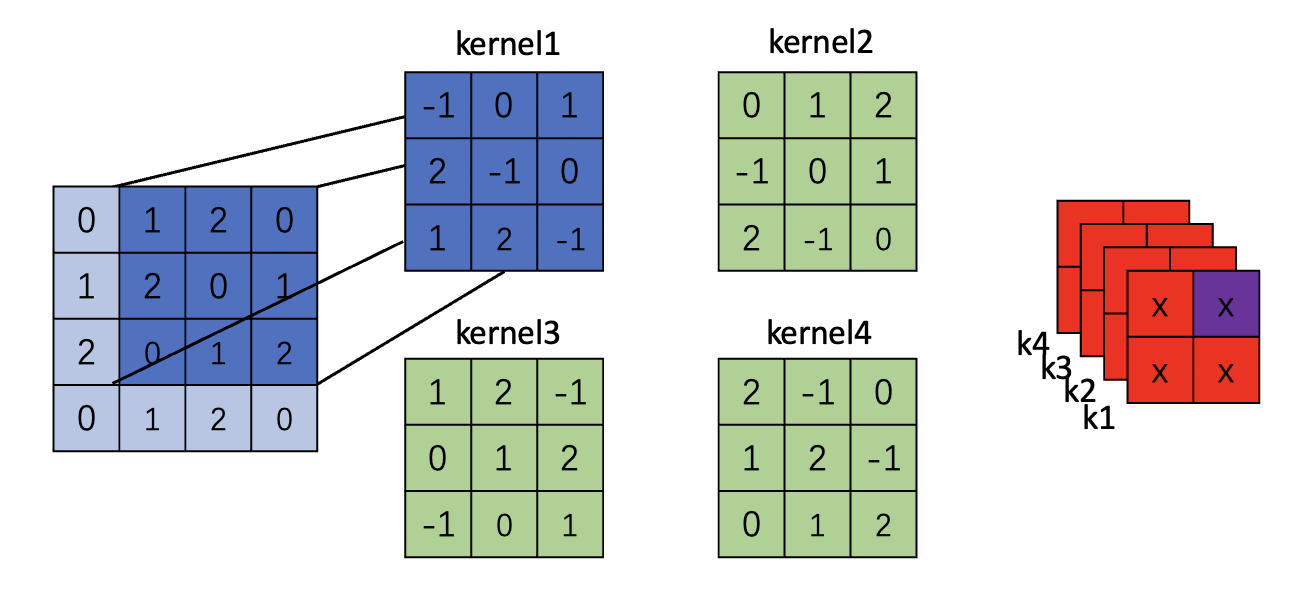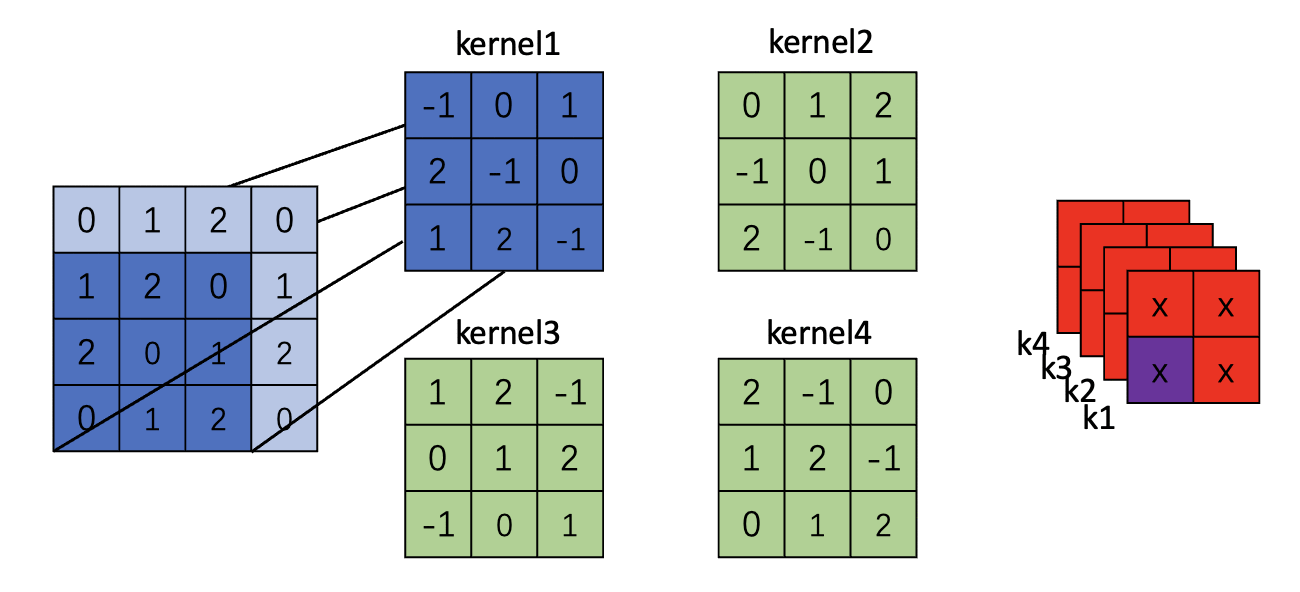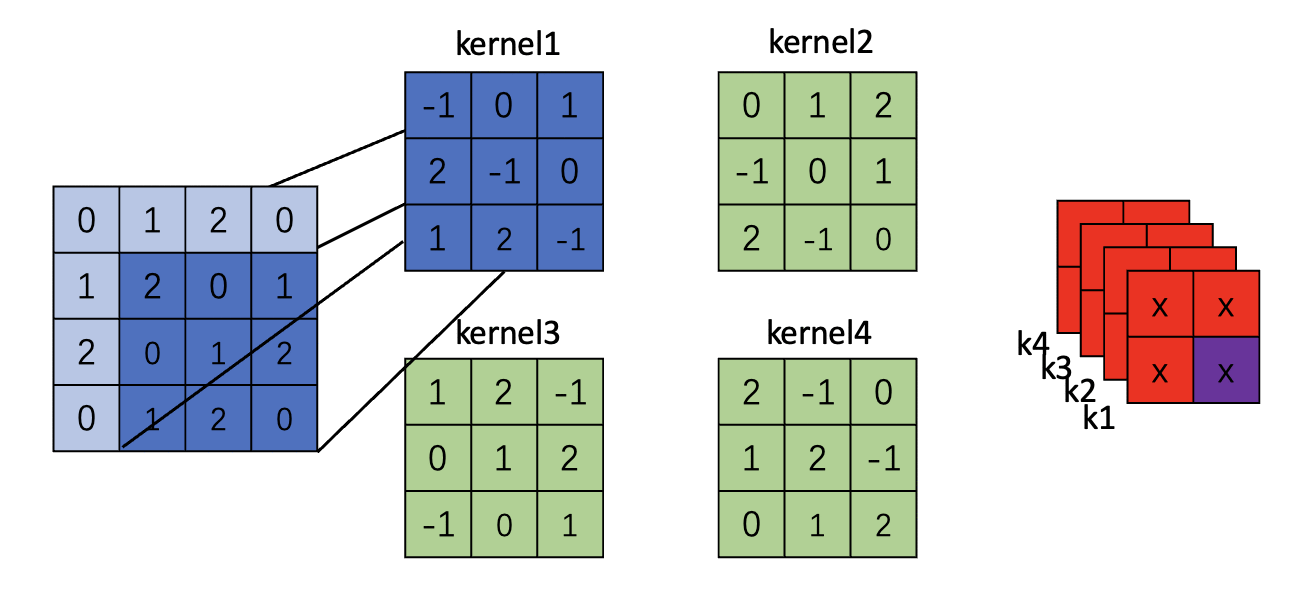
Padding
padding的一个作用是,当我们用kernal size=3 stride=1的卷积核对图片进行操作时,如果不进行padding,最后的特征图会比原图片小,所以要进行padding,padding的方式有四种:
zeros, reflect, replicate, circular
,下面举例说明其区别
首先我们初始化一个(1, 1, 4, 4)的矩阵,之后都对这个矩阵进行操作,其中卷积的权重我们初始化为1,卷积核的大小和数量也为1,这样每次卷积之后输入的矩阵x原来的元素是不会发生变化的
x = torch.nn.Parameter(torch.reshape(torch.arange(0,16,dtype=torch.float), (1,1,4,4)))
'''
Parameter containing:
tensor([[[[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.]]]], requires_grad=True)
'''
zeros
zeros就是填充的每个元素都为0
conv = torch.nn.Conv2d(1,1,1,1,padding=1,padding_mode='zeros',bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
conv(x)
'''
tensor([[[[ 0., 0., 0., 0., 0., 0.],
[ 0., 0., 1., 2., 3., 0.],
[ 0., 4., 5., 6., 7., 0.],
[ 0., 8., 9., 10., 11., 0.],
[ 0., 12., 13., 14., 15., 0.],
[ 0., 0., 0., 0., 0., 0.]]]], grad_fn=<ThnnConv2DBackward>)
'''
reflect
reflect是以矩阵的边为对称轴,填充元素为内部的对称元素
conv = torch.nn.Conv2d(1,1,1,1,padding=1,padding_mode='reflect',bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
conv(x)
'''
tensor([[[[ 5., 4., 5., 6., 7., 6.],
[ 1., 0., 1., 2., 3., 2.],
[ 5., 4., 5., 6., 7., 6.],
[ 9., 8., 9., 10., 11., 10.],
[13., 12., 13., 14., 15., 14.],
[ 9., 8., 9., 10., 11., 10.]]]], grad_fn=<ThnnConv2DBackward>)
'''
replicate
填充元素均为矩阵边上的元素
conv = torch.nn.Conv2d(1,1,1,1,padding=2,padding_mode='replicate',bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
conv(x)
'''
tensor([[[[ 0., 0., 0., 1., 2., 3., 3., 3.],
[ 0., 0., 0., 1., 2., 3., 3., 3.],
[ 0., 0., 0., 1., 2., 3., 3., 3.],
[ 4., 4., 4., 5., 6., 7., 7., 7.],
[ 8., 8., 8., 9., 10., 11., 11., 11.],
[12., 12., 12., 13., 14., 15., 15., 15.],
[12., 12., 12., 13., 14., 15., 15., 15.],
[12., 12., 12., 13., 14., 15., 15., 15.]]]], grad_fn=<ThnnConv2DBackward>)
'''
circular
不好讲,直接看图示结果吧,就是将原数据copy几份围绕在他的周围,然后按照所需的padding裁切
conv = torch.nn.Conv2d(1,1,1,1,padding=2,padding_mode='circular',bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,1,1))
conv(x)
'''
tensor([[[[10., 11., 8., 9., 10., 11., 8., 9.],
[14., 15., 12., 13., 14., 15., 12., 13.],
[ 2., 3., 0., 1., 2., 3., 0., 1.],
[ 6., 7., 4., 5., 6., 7., 4., 5.],
[10., 11., 8., 9., 10., 11., 8., 9.],
[14., 15., 12., 13., 14., 15., 12., 13.],
[ 2., 3., 0., 1., 2., 3., 0., 1.],
[ 6., 7., 4., 5., 6., 7., 4., 5.]]]], grad_fn=<ThnnConv2DBackward>)
'''

Dilated
空洞卷积的函数与Conv的函数相同,唯一的区别就是修改dilation参数,dilation控制kernal中每个元素之间的距离:
这个链接给了一个很好的图示
dilation代表卷积核参数之间的空隙,不理解的可以直接看下图
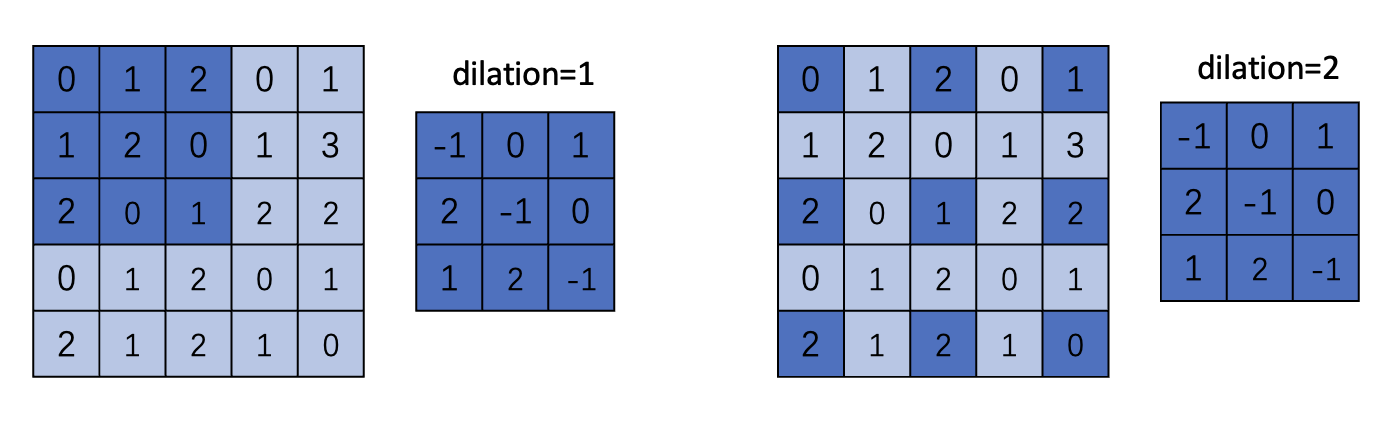
下面通过一个例子展示DilatedConv的执行过程
x = torch.nn.Parameter(torch.reshape(torch.arange(0, 25, dtype=torch.float), (1, 1, 5, 5)))
print(x)
'''
Parameter containing:
tensor([[[[ 0., 1., 2., 3., 4.],
[ 5., 6., 7., 8., 9.],
[10., 11., 12., 13., 14.],
[15., 16., 17., 18., 19.],
[20., 21., 22., 23., 24.]]]], requires_grad=True)
'''
# Conv2d: dilation=1
conv = torch.nn.Conv2d(1, 1, 3, 1, padding=0, dilation=1, bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
print(conv(x))
'''
tensor([[[[ 54., 63., 72.],
[ 99., 108., 117.],
[144., 153., 162.]]]], grad_fn=<ThnnConv2DBackward>)
'''
# Dilate: dilation=2
conv = torch.nn.Conv2d(1, 1, 3, 1, padding=0, dilation=2, bias=False)
conv.weight = torch.nn.Parameter(torch.ones(1,1,3,3))
print(conv(x))
'''
tensor([[[[108.]]]], grad_fn=<SlowConvDilated2DBackward>)
'''
