博客

二叉树前序、中序、后序遍历非递归写法的透彻解析

  • Post author:
  • Post category:其他



前言


在前两篇文章

二叉树

和

二叉搜索树

中已经涉及到了二叉树的三种遍历。递归写法，只要理解思想，几行代码。可是非递归写法却很不容易。这里特地总结下，透彻解析它们的非递归写法。其中，中序遍历的非递归写法最简单，后序遍历最难。我们的讨论基础是这样的：



[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. //Binary Tree Node


  2. typedef




    struct


    node

  3. {


  4. int


    data;


  5. struct


    node* lchild;


    //左孩子


  6. struct


    node* rchild;


    //右孩子

  7. }BTNode;


首先，有一点是明确的：非递归写法一定会用到栈，这个应该不用太多的解释。我们先看中序遍历：




中序遍历




分析


中序遍历的递归定义：先左子树，后根节点，再右子树。如何写非递归代码呢？一句话：

让代码跟着思维走

。我们的思维是什么？思维就是中序遍历的路径。假设，你面前有一棵二叉树，现要求你写出它的中序遍历序列。如果你对中序遍历理解透彻的话，你肯定先找到左子树的最下边的节点。那么下面的代码就是理所当然的：




中序代码段(i)




[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. BTNode* p = root;


    //p指向树根

  2. stack<BTNode*> s;

    //STL中的栈


  3. //一直遍历到左子树最下边，边遍历边保存根节点到栈中


  4. while


    (p)

  5. {

  6. s.push(p);

  7. p = p->lchild;

  8. }



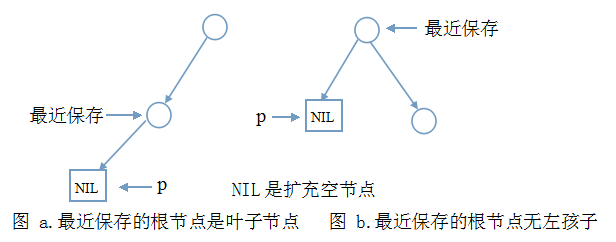
保存一路走过的根节点的理由是：中序遍历的需要，遍历完左子树后，需要借助根节点进入右子树。代码走到这里，指针p为空，此时无非两种情况：





说明：


  1. 上图中只给出了必要的节点和边，其它的边和节点与讨论无关，不必画出。

  2. 你可能认为图a中最近保存节点算不得是根节点。如果你看过

    树、二叉树基础

    ，使用扩充二叉树的概念，就可以解释。总之，不用纠结这个没有意义问题。

  3. 整个二叉树只有一个根节点的情况可以划到图a。

仔细想想，二叉树的左子树，最下边是不是上图两种情况？不管怎样，此时都要出栈，并访问该节点。这个节点就是中序序列的第一个节点。根据我们的思维，代码应该是这样：

[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. p = s.top();

  2. s.pop();

  3. cout << p->data;


我们的思维接着走，两图情形不同得区别对待：


1.图a中访问的是一个左孩子，按中序遍历顺序，接下来应访问它的根节点。也就是图a中的另一个节点，高兴的是它已被保存在栈中。我们只需这样的代码和上一步一样的代码：


[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. p = s.top();

  2. s.pop();

  3. cout << p->data;


左孩子和根都访问完了，接着就是右孩子了，对吧。接下来只需一句代码：p=p->rchild;在右子树中，又会新一轮的代码段(i)、代码段(ii)……直到栈空且p空。



2.再看图b，由于没有左孩子，根节点就是中序序列中第一个，然后直接是进入右子树：p=p->rchild;在右子树中，又会新一轮的代码段(i)、代码段(ii)……直到栈空且p空。

思维到这里，似乎很不清晰，真的要区分吗？根据图a接下来的代码段(ii)这样的：


[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. p = s.top();

  2. s.pop();

  3. cout << p->data;

  4. p = s.top();

  5. s.pop();

  6. cout << p->data;

  7. p = p->rchild;


根据图b，代码段(ii)又是这样的：


[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. p = s.top();

  2. s.pop();

  3. cout << p->data;

  4. p = p->rchild;


我们可小结下：遍历过程是个循环，并且按代码段(i)、代码段(ii)构成一次循环体，循环直到栈空且p空为止。

不同的处理方法很让人抓狂，可统一处理吗？真的是可以的！回顾扩充二叉树，是不是每个节点都可以看成是根节点呢？那么，代码只需统一写成图b的这种形式。也就是说代码段(ii)统一是这样的：




中序代码段(ii)





[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. p = s.top();

  2. s.pop();

  3. cout << p->data;

  4. p = p->rchild;


口说无凭，得经的过理论检验。

图a的代码段(ii)也可写成图b的理由是：由于是叶子节点，p=-=p->rchild;之后p肯定为空。为空，还需经过新一轮的代码段(i)吗？显然不需。(因为不满足循环条件)那就直接进入代码段(ii)。看！最后还是一样的吧。还是连续出栈两次。看到这里，要仔细想想哦！相信你一定会明白的。



这时写出遍历循环体就不难了：

[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. BTNode* p = root;

  2. stack<BTNode*> s;


  3. while


    (!s.empty() || p)

  4. {


  5. //代码段(i)一直遍历到左子树最下边，边遍历边保存根节点到栈中


  6. while


    (p)

  7. {

  8. s.push(p);

  9. p = p->lchild;

  10. }


  11. //代码段(ii)当p为空时，说明已经到达左子树最下边，这时需要出栈了


  12. if


    (!s.empty())

  13. {

  14. p = s.top();

  15. s.pop();

  16. cout << setw(4) << p->data;


  17. //进入右子树，开始新的一轮左子树遍历(这是递归的自我实现)

  18. p = p->rchild;

  19. }

  20. }


仔细想想，上述代码是不是根据我们的思维走向而写出来的呢？再加上边界条件的检测，中序遍历非递归形式的完整代码是这样的：





中序遍历代码一







[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. //中序遍历


  2. void


    InOrderWithoutRecursion1(BTNode* root)

  3. {


  4. //空树


  5. if


    (root == NULL)


  6. return


    ;


  7. //树非空

  8. BTNode* p = root;

  9. stack<BTNode*> s;


  10. while


    (!s.empty() || p)

  11. {


  12. //一直遍历到左子树最下边，边遍历边保存根节点到栈中


  13. while


    (p)

  14. {

  15. s.push(p);

  16. p = p->lchild;

  17. }


  18. //当p为空时，说明已经到达左子树最下边，这时需要出栈了


  19. if


    (!s.empty())

  20. {

  21. p = s.top();

  22. s.pop();

  23. cout << setw(4) << p->data;


  24. //进入右子树，开始新的一轮左子树遍历(这是递归的自我实现)

  25. p = p->rchild;

  26. }

  27. }

  28. }


恭喜你，你已经完成了中序遍历非递归形式的代码了。回顾一下难吗？


接下来的这份代码，本质上是一样的，相信不用我解释，你也能看懂的。




中序遍历代码二




[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. //中序遍历


  2. void


    InOrderWithoutRecursion2(BTNode* root)

  3. {


  4. //空树


  5. if


    (root == NULL)


  6. return


    ;


  7. //树非空

  8. BTNode* p = root;

  9. stack<BTNode*> s;


  10. while


    (!s.empty() || p)

  11. {


  12. if


    (p)

  13. {

  14. s.push(p);

  15. p = p->lchild;

  16. }


  17. else

  18. {

  19. p = s.top();

  20. s.pop();

  21. cout << setw(4) << p->data;

  22. p = p->rchild;

  23. }

  24. }

  25. }




前序遍历




分析


前序遍历的递归定义：先根节点，后左子树，再右子树。有了中序遍历的基础，不用我再像中序遍历那样引导了吧。

首先，我们遍历左子树，边遍历边打印，并把根节点存入栈中，以后需借助这些节点进入右子树开启新一轮的循环。还得重复一句：所有的节点都可看做是根节点。根据思维走向，写出代码段(i):




前序代码段(i)


[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. //边遍历边打印，并存入栈中，以后需要借助这些根节点(不要怀疑这种说法哦)进入右子树


  2. while


    (p)

  3. {

  4. cout << setw(4) << p->data;

  5. s.push(p);

  6. p = p->lchild;

  7. }


接下来就是：出栈，根据栈顶节点进入右子树。




前序代码段(ii)




[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. //当p为空时，说明根和左子树都遍历完了，该进入右子树了


  2. if


    (!s.empty())

  3. {

  4. p = s.top();

  5. s.pop();

  6. p = p->rchild;

  7. }


同样地，代码段(i)(ii)构成了一次完整的循环体。至此，不难写出完整的前序遍历的非递归写法。




前序遍历代码一




[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. void


    PreOrderWithoutRecursion1(BTNode* root)

  2. {


  3. if


    (root == NULL)


  4. return


    ;

  5. BTNode* p = root;

  6. stack<BTNode*> s;


  7. while


    (!s.empty() || p)

  8. {


  9. //边遍历边打印，并存入栈中，以后需要借助这些根节点(不要怀疑这种说法哦)进入右子树


  10. while


    (p)

  11. {

  12. cout << setw(4) << p->data;

  13. s.push(p);

  14. p = p->lchild;

  15. }


  16. //当p为空时，说明根和左子树都遍历完了，该进入右子树了


  17. if


    (!s.empty())

  18. {

  19. p = s.top();

  20. s.pop();

  21. p = p->rchild;

  22. }

  23. }

  24. cout << endl;

  25. }


下面给出，本质是一样的另一段代码：




前序遍历代码二




[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. //前序遍历


  2. void


    PreOrderWithoutRecursion2(BTNode* root)

  3. {


  4. if


    (root == NULL)


  5. return


    ;

  6. BTNode* p = root;

  7. stack<BTNode*> s;


  8. while


    (!s.empty() || p)

  9. {


  10. if


    (p)

  11. {

  12. cout << setw(4) << p->data;

  13. s.push(p);

  14. p = p->lchild;

  15. }


  16. else

  17. {

  18. p = s.top();

  19. s.pop();

  20. p = p->rchild;

  21. }

  22. }

  23. cout << endl;

  24. }


在

二叉树

中使用的是这样的写法，略有差别，本质上也是一样的：




前序遍历代码三


[cpp]


view plain


copy



  1. void


    PreOrderWithoutRecursion3(BTNode* root)

  2. {


  3. if


    (root == NULL)


  4. return


    ;

  5. stack<BTNode*> s;

  6. BTNode* p = root;

  7. s.push(root);


  8. while


    (!s.empty())


    //循环结束条件与前两种不一样

  9. {


  10. //这句表明p在循环中总是非空的

  11. cout << setw(4) << p->data;


  12. /*


  13. 栈的特点：先进后出


  14. 先被访问的根节点的右子树后被访问


  15. */


  16. if


    (p->rchild)

  17. s.push(p->rchild);


  18. if


    (p->lchild)

  19. p = p->lchild;


  20. else

  21. {


    //左子树访问完了，访问右子树

  22. p = s.top();

  23. s.pop();

  24. }

  25. }

  26. cout << endl;

  27. }


最后进入最难的后序遍历：




后序遍历




分析



后序遍历递归定义：先左子树，后右子树，再根节点。后序遍历的难点在于：需要判断上次访问的节点是位于左子树，还是右子树。若是位于左子树，则需跳过根节点，先进入右子树，再回头访问根节点；若是位于右子树，则直接访问根节点。直接看代码，代码中有详细的注释。




后序遍历代码一




[cpp]


view plain


copy



在CODE上查看代码片




派生到我的代码片



  1. //后序遍历


  2. void


    PostOrderWithoutRecursion(BTNode* root)

  3. {


  4. if


    (root == NULL)


  5. return


    ;

  6. stack<BTNode*> s;


  7. //pCur:当前访问节点，pLastVisit:上次访问节点

  8. BTNode* pCur, *pLastVisit;


  9. //pCur = root;

  10. pCur = root;

  11. pLastVisit = NULL;


  12. //先把pCur移动到左子树最下边


  13. while


    (pCur)

  14. {

  15. s.push(pCur);

  16. pCur = pCur->lchild;

  17. }


  18. while


    (!s.empty())

  19. {


  20. //走到这里，pCur都是空，并已经遍历到左子树底端(看成扩充二叉树，则空，亦是某棵树的左孩子)

  21. pCur = s.top();

  22. s.pop();


  23. //一个根节点被访问的前提是：无右子树或右子树已被访问过


  24. if


    (pCur->rchild == NULL || pCur->rchild == pLastVisit)

  25. {

  26. cout << setw(4) << pCur->data;


  27. //修改最近被访问的节点

  28. pLastVisit = pCur;

  29. }


  30. /*这里的else语句可换成带条件的else if:


  31. else if (pCur->lchild == pLastVisit)//若左子树刚被访问过，则需先进入右子树(根节点需再次入栈)


  32. 因为：上面的条件没通过就一定是下面的条件满足。仔细想想！


  33. */


  34. else

  35. {


  36. //根节点再次入栈

  37. s.push(pCur);


  38. //进入右子树，且可肯定右子树一定不为空

  39. pCur = pCur->rchild;


  40. while


    (pCur)

  41. {

  42. s.push(pCur);

  43. pCur = pCur->lchild;

  44. }

  45. }

  46. }

  47. cout << endl;

  48. }

下面给出另一种思路下的代码。它的想法是：给每个节点附加一个标记(left,right)。如果该节点的左子树已被访问过则置标记为left；若右子树被访问过，则置标记为right。显然，只有当节点的标记位是right时，才可访问该节点；否则，必须先进入它的右子树。详细细节看代码中的注释。




后序遍历代码二



[cpp]


view plain


copy



  1. //定义枚举类型：Tag


  2. enum


    Tag{left,right};


  3. //自定义新的类型，把二叉树节点和标记封装在一起


  4. typedef




    struct

  5. {

  6. BTNode* node;

  7. Tag tag;

  8. }TagNode;


  9. //后序遍历


  10. void


    PostOrderWithoutRecursion2(BTNode* root)

  11. {


  12. if


    (root == NULL)


  13. return


    ;

  14. stack<TagNode> s;

  15. TagNode tagnode;

  16. BTNode* p = root;


  17. while


    (!s.empty() || p)

  18. {


  19. while


    (p)

  20. {

  21. tagnode.node = p;


  22. //该节点的左子树被访问过

  23. tagnode.tag = Tag::left;

  24. s.push(tagnode);

  25. p = p->lchild;

  26. }

  27. tagnode = s.top();

  28. s.pop();


  29. //左子树被访问过，则还需进入右子树


  30. if


    (tagnode.tag == Tag::left)

  31. {


  32. //置换标记

  33. tagnode.tag = Tag::right;


  34. //再次入栈

  35. s.push(tagnode);

  36. p = tagnode.node;


  37. //进入右子树

  38. p = p->rchild;

  39. }


  40. else


    //右子树已被访问过，则可访问当前节点

  41. {

  42. cout << setw(4) << (tagnode.node)->data;


  43. //置空，再次出栈(这一步是理解的难点)

  44. p = NULL;

  45. }

  46. }

  47. cout << endl;

  48. }<span style=

    “font-family: ‘Courier New’; ”


    >  </span>




总结


思维和代码之间总是有巨大的鸿沟。通常是思维正确，清楚，但却不易写出正确的代码。要想越过这鸿沟，只有多尝试、多借鉴，别无它法。

以下几点是理解上述代码的关键：

  1. 所有的节点都可看做是父节点(叶子节点可看做是两个孩子为空的父节点)。

  2. 把同一算法的代码对比着看。在差异中往往可看到算法的本质。

  3. 根据自己的理解，尝试修改代码。写出自己理解下的代码。写成了，那就是真的掌握了。