今天我们来看一下子集的问题。
题目描述:给定一个任意集合A,集合的长度为Length,让你打印出这个集合中所包含的所有子集。
题目分析:此问题实际上也是一个遍历树的问题,进行遍历每一个子元素,再进入下层函数时候记录上层结果,加入到下层函数中,再存储起来。其实总结器来他就是一颗完全二叉树。以下我们结合图来具体的说一下:
我们以集合{1,2,3}来对此画树状图理解一下。图如下:
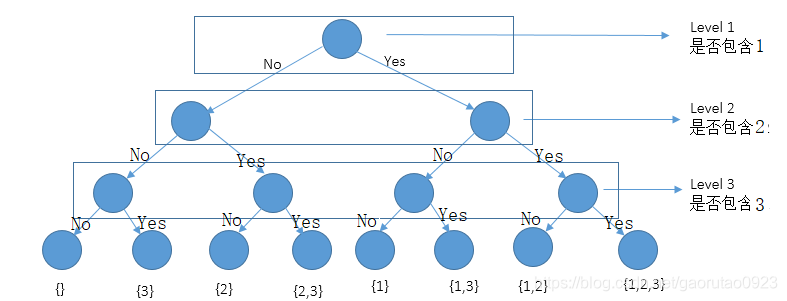
以此我们可以得到集合{1,2,3}中的子集有{},{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3};
以此我们就可以用递归算法对其进行代码操作。
具体的递归方法:对于一个含有n个元素的集合,我们要对其进行找子集,首先我们需要先定义一个数组,以此来存储对这N位的2进制数来表示这个集合,第i为如果为1则表示第i个元素在表示的这个集合中,否则则不再这个集合中。简单的来说就是首先我们先让这个数组的第一个元素为No,然后他会一直往下找,如果到递归结束时还是No,就将它打印出来,然后进行回溯到上一层。然后我们就把这个元素定位Yes,然后在进行在Yes条件下进行递归寻找,我们每次进行到递归结束的条件时,我们对其进行回溯。可能我说的还是有点理解不了,大家可以结合着上面的图来看代码:
#include<stdio.h>
#include<string.h>
#include<assert.h>
int arr[]={0};//存储当前第i个位置元素包含还是不包含
void Ziji(char brr[],int k,int length)//k是递归的层次,k与集合的长度有关
{
assert(arr!=NULL);
if(k==length)//递归结束的条件
{
printf("{ ");
for(int i=0;i<length;i++)
{
if(arr[i]==1)
{
printf("%c ",brr[i]);
}
}
printf("}");
printf("\n");
}
else
{
arr[k]=0;//集合中的第i个元素没有包含,也就是(No)
Ziji(brr,k+1,length); //进行没有被包含(No)的递归
arr[k]=1;//集合中的第i个元素被包含(Yes)
Ziji(brr,k+1,length);//然后进行被包含下(Yes)的递归
}
}
int main()
{
char str[]="ABC";
int lenth=strlen(str);
Ziji(str,0,lenth);
return 0;
}
综上所述呢,我们可以得到一个含有N个元素的集合,它的所有子集的个数为N!个。
大家现在结合着代码是不是理解了此算法的递归操作呢?
如果没理解我再给大家讲一下非递归的算法,我觉得这种办法挺好运的,这种办法就是用C++中的位运算符来进行操作的,上面我们可以得出一个含有N个元素的集合,它的所有子集的个数为N!个,于是我们对其进行移位操作。
如集合A={a,b,c},其子集个数为8;对于任意一个元素,在每个子集中,
要么存在,要么不存在,对应关系是:
a->1或a->0
b->1或b->0
c->1或c->0
映射为子集:
(a,b,c)
(1,1,1)->(a,b,c)
(1,1,0)->(a,b )
(1,0,1)->(a, c)
(1,0,0)->(a )
(0,1,1)->( b,c)
(0,1,0)->( b )
(0,0,1)->( c)
根据以上规律我们可以得出拿一个整形值与一个数进行&操作可以得到我们所需要的子集。进行再一步的观察我们可以看出这个数就是1,每次进行&之后,让这个数进行左移(<<)i位,这个i的初始为0,结束为N,所以我们就可以求出我们所需要的结果,具体代码如下:
#include<stdio.h>
#include<assert.h>
#include<string.h>
int main()
{
char arr[]="ABC";
int a=strlen(arr);
int thm=1<<a;//含有N个元素的子集共有N!个
for(int i=0;i<thm;i++)
{
for(int j=0;j<a;j++)
if(i&1<<j)//每次要对其进行左移操作,然后又i进行&
{
printf("%c",arr[j]);
}
printf("\n");
}
return 0;
}以上的内容就是我对一个集合中求子集问题的所有理解,希望它可以帮助大家。如有错误,请大家评论指正。