选择法和冒泡法是最简单的两种排序算法，易于编写，在处理少量数据时，这两个算法的效率都差不多。但是在处理大量数据时它们效率都不高。快速排序算法是目前效率最高的排序算法，但是编写较为麻烦。

一、选择排序

1、算法描述

选择排序是一种简单直观的排序算法。

选择排序工作原理：升序找最小值，降序找最大值

第一次从待排序的数据元素中选出最小的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小元素，继续放在起始位置直到未排序元素个数为0。

选择排序的思路和插入排序非常相似，也分已排序和未排序区间。但选择排序每次会从未排序区间中找到最小的元素，将其放到已排序区间的末尾。但是不像插入排序会移动数组，选择排序会每次进行交换。

分析：

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)
• 稳定性：不稳定

2、示例

以升序为例：

• 外层循环控制找多少次最小值的下标并将其提到每次的最前面。
• 内层循环控制的是找最小值的下标，将最小值提到每次循环的最前面。
• 
每次内循环找出最小的数，再交换。


代码如下：

	public static void main(String[] args) {
		int[] array = { 7, 8, 6, 9, 0, 4, 3, 1, 2, 5, 10 };

		selectionSort(array);
		System.out.println("最终排序结果为：" + Arrays.toString(array));
	}

	/**
	 * 升序为例
	 * 
	 * @param array
	 */
	public static void selectionSort(int[] array) {
		// 每当完成一轮，将会找到最小值，一个i代表一轮
		for (int i = 0; i < array.length; i++) {
			int minIndex = i;
			// 每一轮从i+1开始找，查找是否有比当前值更小的值
			for (int j = i + 1; j < array.length; j++) {
				if (array[minIndex] > array[j]) {
					minIndex = j;
				}
			}
			// 如果index和i不相等说明，下标交换过，也就是说找到更小的数值了
			if (minIndex != i) {
				swap(array, minIndex, i);
			}
			System.out.println("第 " + i + " 次的排序结果为：" + Arrays.toString(array));
		}
	}

	private static void swap(int[] array, int i, int j) {
		int temp = array[i];
		array[i] = array[j];
		array[j] = temp;
	}

二、冒泡排序

1、算法描述

冒泡排序的思想：

冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复n次，就完成了n个数据的排序工作。

冒泡排序工作原理：

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 每一轮对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。第一轮结束，最后的元素应该会是最大的数。
3. 针对所有的元素重复以上的步骤n-1轮，分别倒序排好倒数第二大、倒数第三大……的元素。直到没有任何一对数字需要比较。

分析：

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)
• 稳定性：稳定

2、示例

以升序（求最大值）为例：

• 外层循环控制的是排序次数，内层循环控制的是求最大值 。
• 
内循环找到最大值，则马上交换，依次执行。


代码如下：

    public static void main(String[] args) {
        int[] array = { 7, 8, 6, 9, 0, 4, 3, 1, 2, 5, 10 };
        bubbleSort(array);
        //bubbleSort2(array);
        System.out.println("最终排序结果为：" + Arrays.toString(array));
    }

    /**
     * 升序为例
     * @param array
     */
    private static void bubbleSort(int[] array) {
        // 进行 array.length - 1轮比较
        for (int i = 0; i < array.length - 1; i++) {
            //array.length - 1 - i后面排序好的就不用比较了。
            for (int j = 0; j < array.length - 1 - i; j++) {
                //当前值大于后一位的值，则交换。 >是稳定的， >=是不稳定的。
                if(array[j] > array[j + 1]){
                    swap(array, j, j + 1);
                }
            }
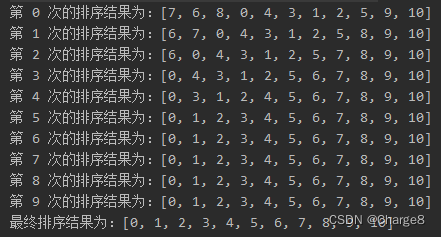
            System.out.println("第 " + i + " 次的排序结果为：" + Arrays.toString(array));
        }
    }

    private static void swap(int[] array, int i, int j) {
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }


冒泡优化：

如果每轮排序之后都没有交换值，则排序完成，结束外层循环。

    private static void bubbleSort2(int[] array) {
        // 进行 array.length - 1轮比较
        for (int i = 0; i < array.length - 1; i++) {
            //如果每轮排序之后都没有交换值，则排序完成
            boolean flag = false;
            for (int j = 0; j < array.length - 1 - i; j++) {
                //当前值大于后一位的值，则交换值。 >是稳定的， >=是不稳定的。
                if(array[j] > array[j + 1]){
                    swap(array, j, j + 1);
                    flag = true;
                }
            }
            if(!flag) {
                break;
            }
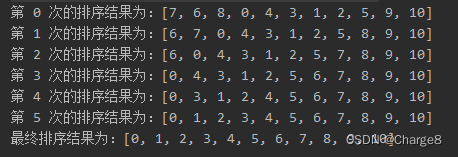
            System.out.println("第 " + i + " 次的排序结果为：" + Arrays.toString(array));
        }
    }

三、快速排序

1、算法描述

算法描述：

每次都设第一个数为基数，然后把小于这个值的移到左边（左边的为乱序），大于这个值的移到右边(右边的也为乱序)。

快速排序的执行流程主要分为如下三步：

1. 从数列中选取一个数作为基数用于比较，记为cardinal
2. 将大于cardinal的数全部放在右边，将小于或等于cardinal的数全部放在左边，进行分区
3. 再对左右两边的分区重复进行第二步，直到各分区只有一个数

分析：

• 时间复杂度：O(nlogn)， 最坏的情况（在原数组有序的情况下）就是O(n^2)
• 空间复杂度：O(n)
• 稳定性：不稳定

2、示例

以升序为例：

快速排序是基于分治策略的，分治策略常用的解决方法就是二分法、递归解决。

代码如下：

	public static void main(String[] args) {
		int[] array = { 45, 28, 80, 90, 50, 16, 100, 10 };
		quickSort(array, 0, array.length - 1);
		System.out.println("最终排序结果为：" + Arrays.toString(array));
	}

	/**
	 * 快速排序
	 *
	 * @param array
	 *            - 数组
	 * @param left
	 *            - 数组的左端
	 * @param right
	 *            - 数组的右端
	 */
	public static void quickSort(int[] array, int left, int right) {
		// 将数组拆分成只有一个元素，就不用再拆了
		if (left >= right) {
			return;
		}
		int middleIndex = sort(array, left, right);
		// int middleIndex = sort2(array, left, right);
		System.out.println("中间值 " + array[middleIndex] + "，中间索引 " + middleIndex + " 的排序结果为：" + Arrays.toString(array));
		// 得到中间值index，然后一分为二，继续递归拆分
		quickSort(array, left, middleIndex - 1);
		quickSort(array, middleIndex + 1, right);
	}

	/**
	 * 比较过程中直接交换基数值
	 * 
	 * @param array
	 * @param left
	 * @param right
	 * @return
	 */
	private static int sort(int[] array, int left, int right) {
		// 每次以左边的a[left]为基准数，不能用array[0]。
		int base = array[left];
		while (left < right) {
			// 开始从右往左找到第一个小于基数的数停下，交换值
			while (left < right && array[right] >= base) {
				right--;
			}
			swap(array, right, left);
			// 开始从左往右找到第一个大于基数的数停下，交换值
			while (left < right && array[left] <= base) {
				left++;
			}
			swap(array, right, left);
		}
		// 此时left和right相遇，即相同返回
		return left;
	}

	private static void swap(int[] array, int i, int j) {
		int temp = array[i];
		array[i] = array[j];
		array[j] = temp;
	}

上面 sort方法是基于比较过程中直接交换基数值。

下面 sort方法也可以基于比较过程中交换比较值，最后设置基数值。

	/**
	 * 比较过程中交换比较值，最后设置基数值
	 * 
	 * @param array
	 * @param left
	 * @param right
	 * @return
	 */
	public static int sort2(int[] array, int left, int right) {
		// 每次以左边的a[left]为基准数
		int base = array[left];
		while (left < right) {
			// 从right所指位置向前搜索找到第一个关键字小于base的记录和base互相交换
			while (left < right && array[right] >= base) {
				right--;
			}
			array[left] = array[right];
			// 从left所指位置向后搜索，找到第一个关键字大于base的记录和base互相交换
			while (left < right && array[left] <= base) {
				left++;
			}
			array[right] = array[left];
		}
		// 此时left和right相遇，将base值放到left与right相同的位置。
		array[left] = base;
		return left;
	}

– 求知若饥，虚心若愚。