[XJTU计算机网络安全与管理]——第六讲 伪随机数,流密码,哈希
一、随机数
随机数
随机数(random numbers)在密码学中有着丰富的
应用
1️⃣ 在认证协议中用于抵御重放攻击——三种方法:序列号、时间戳、随机数挑战应答
2️⃣ 会话密钥(尽量少的重复)
3️⃣ 公钥生成
4️⃣ 一次一密的密码流
在任意情况下,其值都应严格遵从以下特点
满足随机性(random),一致传播(uniform distribution),独立(independent)
不可预测性
TRNG、PRNG和PRF
下图把一个
真随机数生成器TRNG和两种伪随机数生成器PRNG、PRF
进行了对比。
TRNG把一个很随机的源作为输入,这个源常称为熵源,本质上,熵源是从计算机的物理环境抽取的,可能包括键盘敲击时间模式,磁盘的电活动,鼠标移动,系统时间的瞬时值等。源或诸源的组合作为算法的输入,产生随机的二元输出。TRNG也许仅仅是把模拟信号源转化为二元输出。TRNG也可能会做额外的处理以消除源里的不平衡。
相反,
PRNG取一个固定值,称为种子作为输入,用一个确定性的算法产生位输出序列
。通常,如图显示有反馈路径,由此算法的
部分结果反馈作为输入
,而其他部分作为输出位。需要注意的是输出位流仅仅由输入值决定,所以知道算法和种子的敌手可以重现整个位流。
下图显示了两款基于应用的不同形式的PRNG。
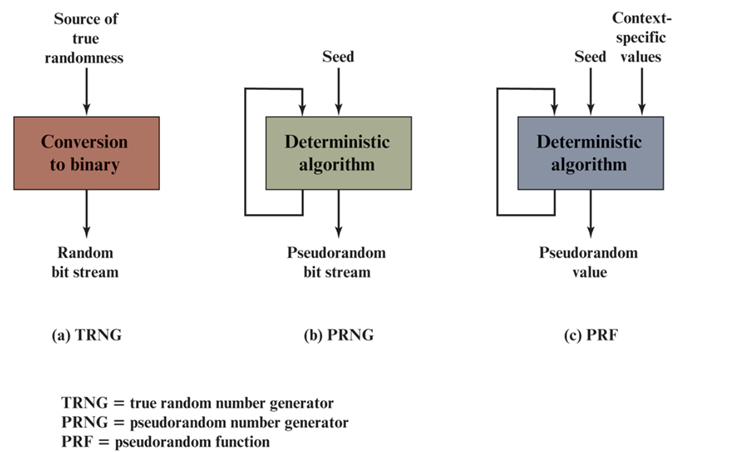
1️⃣ 伪随机数生成器用于
生产不限长位流
的算法称为PRNG。不限长位流的通常应用是作为对称流密码的输入,如同8.4节所讨论的那样,也可参见图4.1(a)。
2️⃣ 伪随机函数(PRF)PRF
用于产生固定长度
的伪随机位串。对称加密密钥和时变值就是例子。通常PRF的输入为种子加上一些上下文相关的特定值,如用户D或应用D。
除了产生位的数量外,PRNG和PRF之间没有差别。这两个应用可以使用相同的算法。两者都需要种子,都必须具有随机性和不可预测性。而且,PNG应用可能也需要使用上下文相关的输入。接下来,我们
对这两个应用不做区别。
伪随机数生成器PRNG
伪随机数生成器 Pseudorandom Number Generators (PRNGs)
通常采用确定性的算法技术以生成“随机数”
尽管不是真正的“随机”
但是能够通过多种“随机性”测试
被称为“伪随机数”;通过“伪随机数生成器”生成
PRNG的要求
随机性:均匀性;可伸缩性;一致性
不可预测性:正向不可预测反向不可预测
种子的要求:不可预测,应为随机或伪随机数
线性同余生成器Linear Congruential Generator——了解
该方案随机数序列采用如下迭代技术生成
X
n
+
1
=
(
a
X
n
+
c
)
mod
m
X_{n+1}=(aX_n+c)\ \text{mod}\ m
X
n
+
1
=
(
a
X
n
+
c
)
mod
m
通过给定相应的参数可以获得像随机(random-like)的数(通常m较大,是一个接近或等于2
31
的数
评价一个随机数生成器的准则:
这个函数应当是一个完整周期的生成函数、
产生的序列应当是看上去随机的(a=7
5
=16807)这个函数应当采用32bit算术高效实现
攻击者可以通过获取少量的值重构序列(比如同余方程)
可复杂化:修改m(比如将其与系统时钟联系)
BBS生成器Blum Blum Shub Generator——了解
基于公钥密码算法
它从迭代中取出最低比特位
x
i
=
x
i
−
1
2
mod
n
x_i=x_{i-1}^2\ \text{mod}\ n
x
i
=
x
i
−
1
2
mod
n
不可预测,能通过next-bit 测试。
基于N的分解困难。
非常慢。因为用到了大数
.
加密器使用太慢,可用作密钥生成。
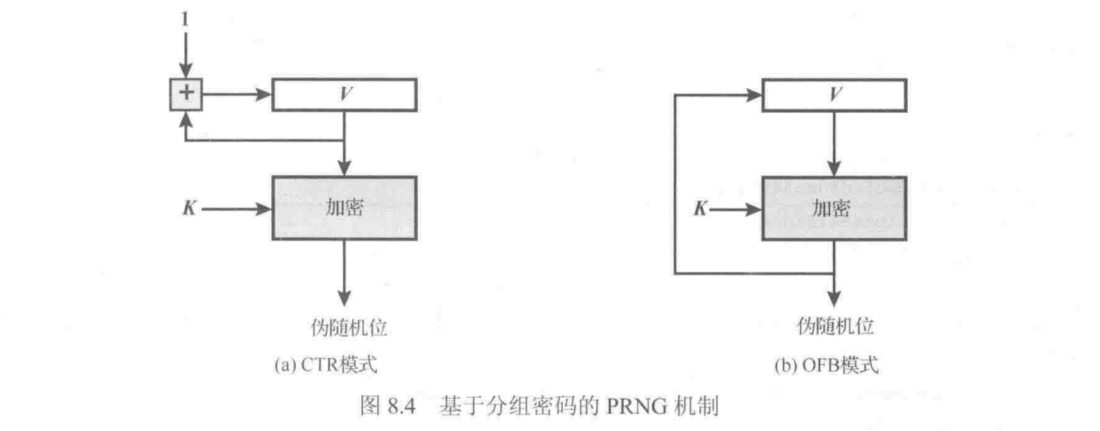
利用块加密技术的伪随机数生成器
在密码学应用当中,可以采用块加密器(block cipher)生成随机数
常用来从
主密钥(长期保存的密钥
)(master key 生成
会话密钥(真正用的密钥)
)
1️⃣
计数器模式(Counter Mode)
——CTR
X
i
=
E
k
m
[
i
]
X_i=E_{km}[i]
X
i
=
E
k
m
[
i
]
2️⃣
输出反馈模式(Output Feedback Mode)
——OFB
X
i
=
E
k
m
[
X
i
−
1
]
X_i=E_{km}[X_{i-1}]
X
i
=
E
k
m
[
X
i
−
1
]
真随机数生成器
最好的资源是真实世界中的自然随机
寻找经常性的与随机性的事件并进行监控
常常需要特别的设备以完成:比如,辐射计数器,电磁噪声,音频噪声,二极管热噪声等等
比较新的cpu中包含了这样的组件
信号的非平坦
在采样与使用时需要进行补偿
最好每次采样仅用若干噪音比特
二、流密码
一个典型的流密码每次加密一个字节的明文
,当然流密码也可被设计为每次操作一位或者大于一字节的单元。下图给出了一个典型的流密码的结构图。在该结构中密钥输入到一个伪随机数(位)发生器,该伪随机数生成器产生一串随机的8位数。生成器的输出称为密钥流,密钥流和明文流的每一个字节进行按位异或运算,得到一个密文字节。
例如,如果发生器产生的下一字节为01101100,而下一明文字节为11001100,则得出的密文字节为
11001100
明
文
⊕
01101100
‾
密
钥
流
10100000
密
文
\begin{aligned} &11001100 &明文\\ \oplus\ &\underline{01101100} &密钥流\\ &10100000 &密文\\ \end{aligned}
⊕
1
1
0
0
1
1
0
0
0
1
1
0
1
1
0
0
1
0
1
0
0
0
0
0
明
文
密
钥
流
密
文
解密需要使用相同的伪随机序列
10100000
密
文
⊕
01101100
‾
密
钥
流
11001100
明
文
\begin{aligned} &10100000 &密文\\ \oplus\ &\underline{01101100} &密钥流\\ &11001100 &明文\\ \end{aligned}
⊕
1
0
1
0
0
0
0
0
0
1
1
0
1
1
0
0
1
1
0
0
1
1
0
0
密
文
密
钥
流
明
文
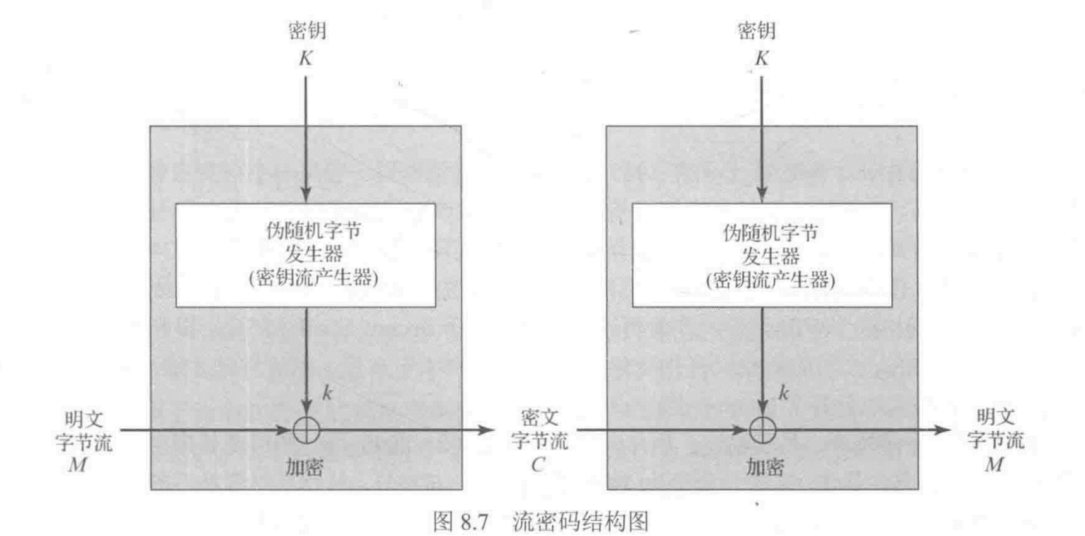
流密码类似于“一次一密”,不同的是“一次一密”使用的是真正的随机数流,而流密码使用的是伪随机数流。
特点
设计准则应该满足:
长时期的不重复
较强的统计随机性
依赖于足够大的密钥
较大的线性复杂度
设计恰当的话能达到不亚于块加密的效果
简便高速
RC4算法
Ron Rivest设计,简单高效
可变密钥长度,面向字节的
广泛应用(ssl,wep)
密钥构成对8比特数据的置换
每次一个字节将报文进行置换乱排
作业题。
初始化S
/*初始化*/
for i = 0 to 255 do
S[i] = i
T[i] = K[i mod keylen];
/*S的初始置换*/
j = 0
for i = 0 to 255 do
j = (j + S[i] + T[i]) (mod 256)
swap (S[i], S[j])
密钥流的产生
/*密钥流的生成*/
i = j = 0
while(true)
i = (i + 1) (mod 256)
j = (j + S[i]) (mod 256)
swap(S[i], S[j])
t = (S[i] + S[j]) (mod 256)
k=S[t];
安全性
对已知攻击方式抵御较好
很好的非线性
不可重用密钥
WEP的应用问题
使用反馈移位寄存器的流密码
基于反馈移位寄存器(FSR)的流密码表现得性能非常适用于紧凑的硬件实现
。
FSR由一系列1位存储单元构成。每个单元有一条输出线和一条输入线,其中输出线指示当前存储的值。在离散时刻(时钟时间),每个存储设备中的值被替换为输入线指示的值。结果如下:最右(最低有效)位被移出,作为该时钟周期的输出位,其它位右移一位。然后根据FSR种的其它位重新计算最左(最高有效位)
线性反馈移位寄存器LDSR
若f(x+y)=f(x)+f(y)且af(x)=f(ax),则f是线性的
B
n
=
A
1
B
n
−
1
A
2
B
n
−
2
.
.
.
A
n
B
0
=
∑
i
=
1
n
A
i
B
i
−
1
B_n=A_1B_{n-1}A_2B_{n-2}…A_nB_0=\sum_{i=1}^nA_iB_{i-1}
B
n
=
A
1
B
n
−
1
A
2
B
n
−
2
.
.
.
A
n
B
0
=
i
=
1
∑
n
A
i
B
i
−
1
要会用多项式查找生成序列
P
(
X
)
=
1
+
A
1
X
+
A
2
X
2
+
.
.
.
+
A
n
−
1
X
n
−
1
+
A
n
X
n
=
1
+
∑
i
=
1
n
A
i
X
i
P(X)=1+A_1X+A_2X^2+…+A_{n-1}X^{n-1}+A_nX^n=1+\sum_{i=1}^nA_iX^i
P
(
X
)
=
1
+
A
1
X
+
A
2
X
2
+
.
.
.
+
A
n
−
1
X
n
−
1
+
A
n
X
n
=
1
+
i
=
1
∑
n
A
i
X
i
特征多项式的性质是,取多项式的倒数后可以查找对应LDSR的生成序列
例如:1+X+X
3
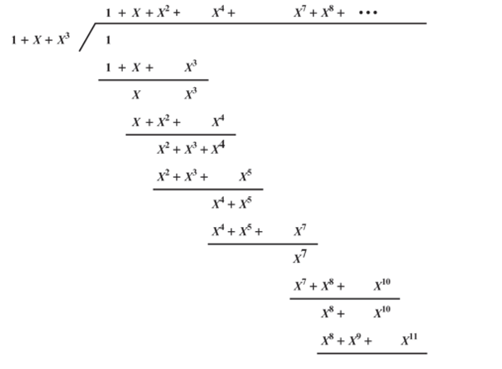
生成111010011…
非线性反馈移位寄存器NDSR——了解
对于NFSR,系数可以是变量
例如
B
5
=
B
4
⊕
B
3
B
2
B_5=B_4\oplus B_3B_2
B
5
=
B
4
⊕
B
3
B
2
等效表示为
P
(
X
)
=
1
+
X
+
X
2
X
4
P(X)=1+X+X^2X^4
P
(
X
)
=
1
+
X
+
X
2
X
4
Grain-128a——了解
Grain是一系列
硬件效率
的流密码。
Grainv1的规范定义了两种流密码:
80位密钥和一个64位初始化向量(IV)
128位密钥和一个80位的IV
Grain-128a针对身份认证进行了修订和扩展
由两个移位寄存器(一个线性反馈,另一个具有非线性反馈)和一个滤波组成
三、密码学哈希函数
哈希函数H使用变长数据分组M作为输入,生成定长结果
h
=
H
(
M
)
h=H(M)
h
=
H
(
M
)
。这一结果称为哈希值或哈希码
密码学哈希函数要求在以下两种情况下计算上的不可行
找到一个映射为某个哈希结果的数据对象(单向性)——不可逆
找到两个映射为相同哈希结果的数据对象(抗碰撞性)
哈希函数的应用——重要
密码学哈希函数的应用:消息认证;数字签名;其他应用(密码存储)
消息认证
消息认证是用来验证消息完整性的一种机制或服务
1️⃣ 保证收发的数据的一致性(保证没有
修改,插入,删除或重放
)。2️⃣ 保证发送方生成的身份的真实有效
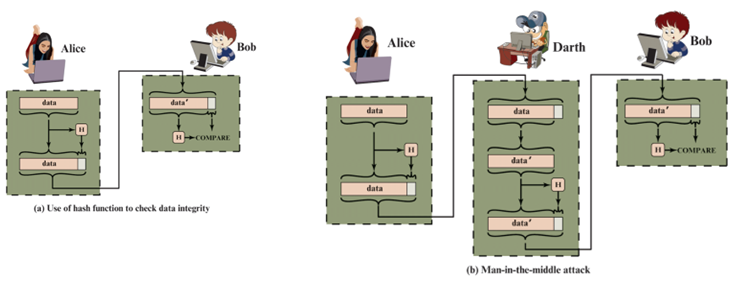
消息认证中使用Hash函数的本质如下:发送者根据待发送的消息使用该函数计算一组Hash值,然后将Hash值和消息一起发送过去。接收者收到后对于消息执行同样的Hash计算,并将结果与收到的Hash值进行对比。如果不匹配,则接收者推断出消息(当然也可能是Hash值)遭受了篡改[参见下图]。
?
Hash函数的运算结果必须通过安全的方式传输
。因为Hash函数必须得到保护,使得如果攻击者篡改或替换消息的话,对于攻击者不能够轻易地同时对Hsh值进行修改以蒙骗接收者。这种类型的攻击如图(b)所示。该例中,Alice传输消息时附上数据的Hash值。Darth拦截了该消息,篡改或替换其中的数据,然后重新计算Hash值并附在后面。Bob收到篡改后的数据块以及新的Hash值,未能发现消息已经被篡改。为了防止该类攻击,
由Alice生成的Hash值必须得到保护。
——防止中间人攻击。
当哈希函数用于提供消息认证功能时,哈希函数通常称为
消息摘要
哈希码提供的认证方案
1️⃣
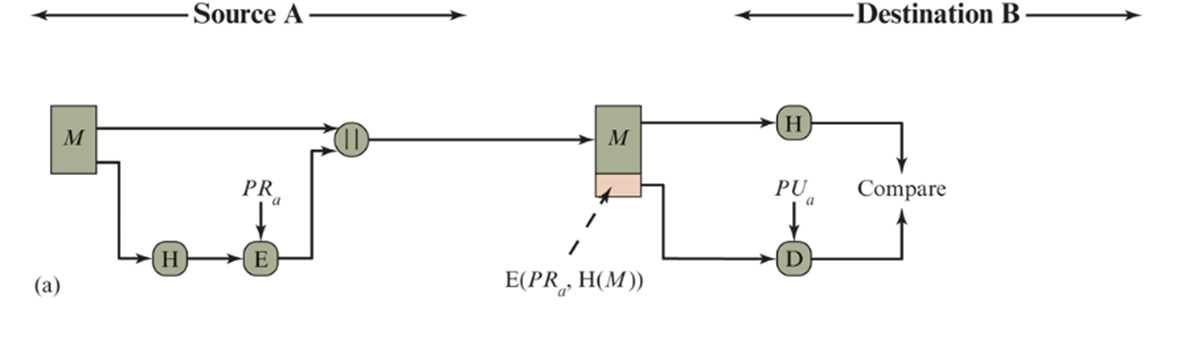
使用对称加密提供消息认证
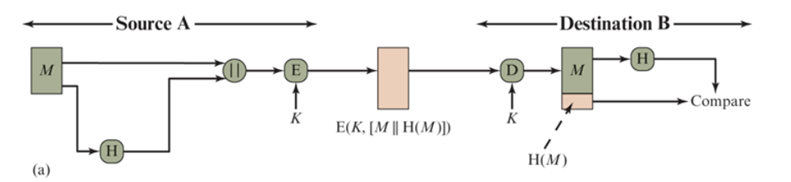
**使用对称密码算法E加密消息和Hash码。**因为只有A和B共享密钥K,所以消息必然是发自A处,并且未被更改过。这里附加的Hash码提供了实现认证功能的结构。因为对于整个消息以及Hash码都使用了加密,
保密性也被提供
。
防止了中间人攻击。
2️⃣
只使用对称加密算法E加密哈希函数。
(
不强调机密性情况下可有效降低运算开销
)
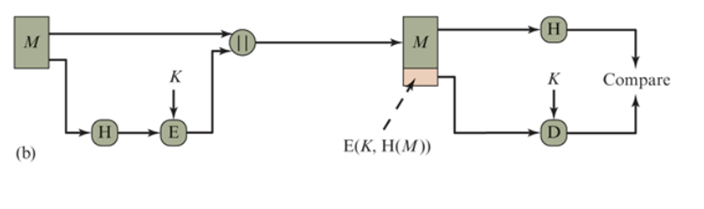
适用于强调真实性>保密性:例如档案
——不怕被看,怕被改
使用对称密码算法E
只对Hash码进行加密
。对于无须保密性的应用,这种方案减少了加解密操作的负担。
3️⃣
只使用哈希函数实现消息认证(结合共享秘密值)
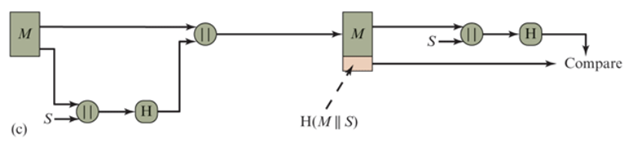
不使用加密算法,仅使用Hsh函数也能够实现消息认证。该方案假设通信双方共享相同的秘密值S。
发送方A将消息M和秘密值S串联后计算其Hash值,并将得到的Hash值附在消息M后发送
。因为接收方B同时掌握S,所以能够重新计算该Hash值进行验证。由于秘密值S本身并没有在信道传送,攻击者不能够对在信道上拦截的消息进行修改,进而也不能制作假消息。
message同样是使用明文传输,
适用于强调真实性>保密性
4️⃣
加密整个消息和哈希值(为上面的方案提供机密性)

通过将整个消息和Hash值加密,能够在方案©的基础上提供保密性。
数字签名
同消息认证应用类似,对于Hash函数的另外一个重要应用就是数字签名。数字签名的操作与MAC相似,在进行数字签名过程中使用用户的
私钥加密消息的Hash值
,其他任何知道该用户公钥的人都能够**通过数字签名来验证消息的完整性。**在这种情况下,攻击者要想篡改消息,则需要知道用户的私钥。数字签名的应用比消息认证更为广泛。
数字签名有如下两种方法:
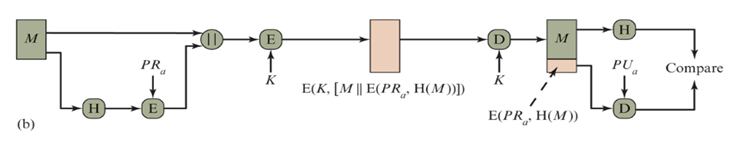
1️⃣ 使用发送方的私钥,利用公钥密码算法仅对Hash码进行加密。这种方法可提供认证:由于只有发送方可以产生加密后的Hash码,所以这种方法也提供了数字签名,事实上,这就是数字签名技术的本质所在。
2️⃣ 若
既希望保证保密性又希望有数字签名
,则先用发送方的私钥对Hash码加密,再用对称密码中的密钥对消息和公钥算法加密结果进行加密,
这种技术比较常用。
其他应用
用于生成单向口令文件
用于入侵检测与病毒扫描
构建随机函数(PRF)(用于生成对称密钥)或伪随机数生成器(RPNG)
简单哈希函数的构造——了解一下
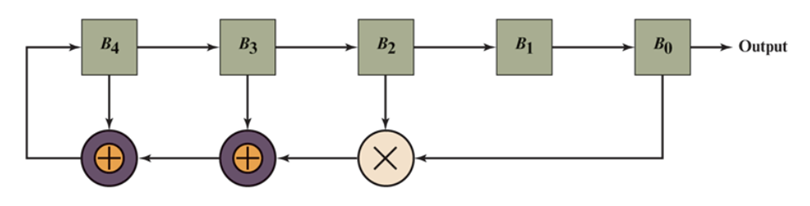
纵向冗余检验
把包文数据划分为若干n比特定长分组的B1,B2,… ,Bm 。
哈希函数值C的每一个位实际上是各数据分组对应位的一个简单的奇偶检验 ,即
C
(
i
)
=
B
1
(
i
)
+
B
2
(
i
)
+
…
+
B
m
(
i
)
其
中
,
i
=
1
,
2
,
…
,
n
;
C
(
i
)
为
C
的
第
i
位
。
C_{(i)} = B_1{(i)} + B_2{(i)} + … +B_m{(i)} \\ 其中, i = 1,2,…,n;\quad C(i) 为C的第i位。
C
(
i
)
=
B
1
(
i
)
+
B
2
(
i
)
+
…
+
B
m
(
i
)
其
中
,
i
=
1
,
2
,
…
,
n
;
C
(
i
)
为
C
的
第
i
位
。
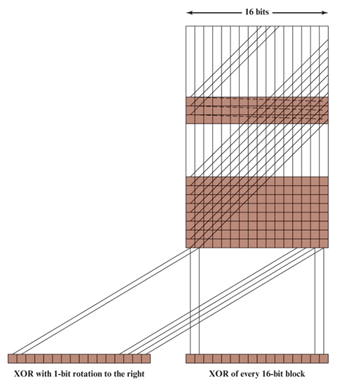
循环移位
C
0
=
0
C_0=0
C
0
=
0
初始值。
C
i
=
R
O
R
(
C
i
−
1
)
⊕
M
i
,
i
=
1
,
.
.
.
,
n
C_i=ROR(C_{i-1})\oplus M_i,i=1,…,n
C
i
=
R
O
R
(
C
i
−
1
)
⊕
M
i
,
i
=
1
,
.
.
.
,
n
ROR( ) 表示循环右移 1 位。
H
(
M
)
=
C
n
H(M)=C_n
H
(
M
)
=
C
n
将输入数据完全随机化,掩盖了数据中规则化的信息。
密码分组链接(CBC)——不用密钥
算法过程:
将报文 M划分成固定长度的分组
M
1
,
M
2
,
.
.
.
,
M
N
M_1,M_2,…,M_N
M
1
,
M
2
,
.
.
.
,
M
N
;
采用类似DES加密的算法来计算哈希码C:
H0
H_0
H
0
为初始值
Hi
=
E
M
i
(
H
i
−
1
)
H_i=E_{Mi}(H_{i-1})
H
i
=
E
M
i
(
H
i
−
1
)
C=
H
N
(
哈
希
码
)
C=H_N(哈希码)
C
=
H
N
(
哈
希
码
)
哈希函数的安全性
对哈希函数的生日攻击:生日悖论
生日悖论
在一个人群中(人数为
k
),问其中至少有两个人生日相同的概率有多少?
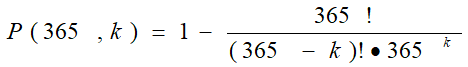
从另一个角度:
k
为何值可以使人群中至少存在两个人生日相同的概率大于 50%?
答案是
k
= 23 ,这个概率要比许多人的直觉猜测的大得多。
这个问题可以说明:有时候概率计算的结果是与一般人的直觉相违背的
密码分析和安全哈希函数
密码分析攻击试图哈希函数或MAC算法的某些特性来进行攻击而不是进行强行搜索。
理想的算法抗密码分析攻击的强度应不小于其抗强行攻击的强度,即采用密码分析攻击的难度要大于或等于采用强行攻击的难度。
近年来形成了一些具有代表性的安全哈希函数的设计结构。
安全哈希函数
一个迭代的哈希函数。
将输入报文分为
L
个定长
b
比特的分组$Y_0, Y_1,… ,Y_{L-1} $。
最后一个分组需要填充至
b
比特。最后一个分组包含了哈希函数H( ) 的输入总长度。
哈希算法中重复使用了一个压缩函数
f
,
f
( ) 的输人是前一轮的
n
比特输出(称为链接变量)以及当前的
b
比特分组,输出为
n
比特的链接变量值。
SHA
SHA由1993年由NIST提出作为联邦信息标准
1995年修订版
SHA-1生成160bit哈希函数
2002年NIST发布修订版
SHA-2
将哈希函数长度定义为三个版本
包括256位,384位和512位(最常用)。
2005年NIST宣布逐步废除SHA-1,在2010年使用SHA-2.但实际上直至2017年在得到广大主流厂商的相应。
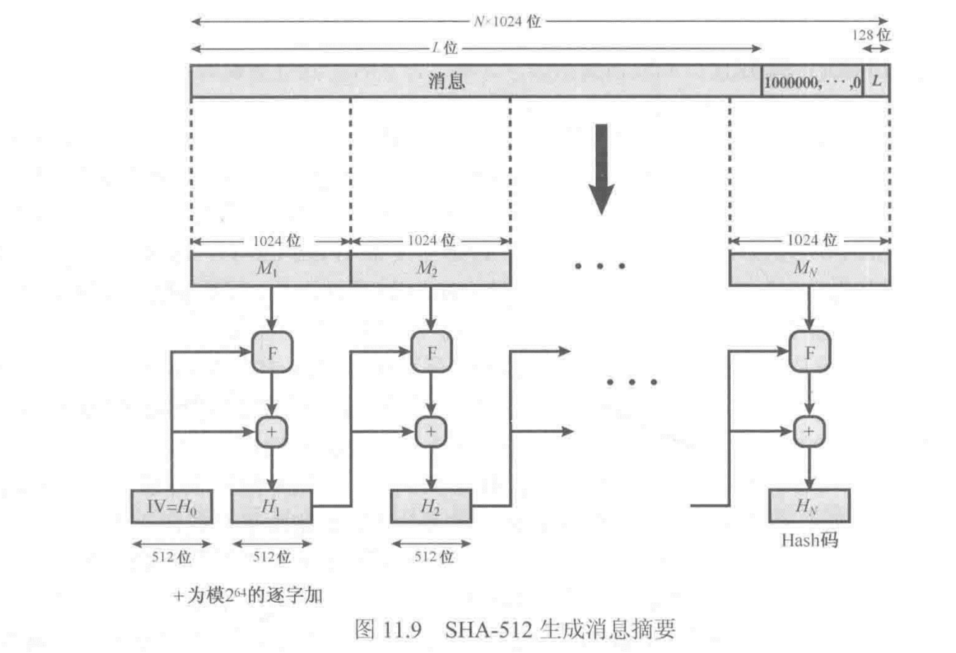
SHA-512逻辑
与MD5 逻辑结构一致
1️⃣ 附加填充位:即填充后的报文长度
K
对1024取模等于896(
K
mod 1024 = 896)。填充的比特模式为第一位为1其余各位为0,即100…0。
2️⃣ 附加长度:附加在消息后面,将其视为一个128位的无符号整数,它包含填充前原始消息的长度
3️⃣ 初始化哈希缓冲区:存储中间结果与最终结果,缓冲区由8个64位寄存器表示(有初值)。
4️⃣ 以1024位的分组为单位处理消息:80轮
输出:
H
0
=
I
V
H
i
=
S
U
M
64
(
H
i
−
1
,
a
b
c
d
e
f
g
h
i
)
M
D
=
H
N
H_0=IV\\ H_i=SUM_{64}(H_{i-1},abcdefgh_i)\\ MD=H_N
H
0
=
I
V
H
i
=
S
U
M
6
4
(
H
i
−
1
,
a
b
c
d
e
f
g
h
i
)
M
D
=
H
N
SHA-512轮函数

参考资料
[1] 西安交通大学计算机网络安全与管理2022年春PPT 田暄
[2] 密码编码学与网络安全(第七版),William Stallings著,王后珍等译