设计一个函数,该函数用于求一个任意大小的二维double型数组的平均值。
该函数的名字叫做matrixAvg
int main() {
double matrixAvg(int m, int n, double b[m][n]);
int M, N;
scanf(“%d%d”, &M, &N);
double aver, a[M][N];
int i, j;
for (i = 0; i < M; i++)
for (j = 0; j < N; j++)
scanf(“%lf”, &a[i][j]);
aver = matrixAvg(M, N, a);
printf(“%.2f\n”, aver);
return 0;
}
double matrixAvg(int m, int n, double b[m][n])
{
int i, j;
double sum = 0, num;
for (i = 0; i < m; i++)
{
for (j = 0; j < n; j++)
{
sum = sum + b[i][j];
}
}
num = sum / (m * n);
return num;
}
设计一个函数,该函数用于实现一维数组的循环右移。
函数原型为:
void arrayShiftRight(int a[ ],int n,int m);
该函数的功能是将长度为n的数组a循环右移m个位置。
#include<stdio.h>
void arrayShiftRight(int n, int m,int x[])
{
int t=0,i=0,j=1;
for(i=0;i<m;i++)
{
t=x[n-1];
for(j=n-2;j>-1;j–)
{
x[j+1]=x[j];
}
x[0]=t;
}
}
int main()
{
int n,k,xx[20];
int i,j,t;
scanf(“%d”,&n);
scanf(“%d”,&k);
for(i=0;i<n;i++)
{
scanf(“%d”,&xx[i]);
}
arrayShiftRight(n,k,xx);
for(i=0;i<n;i++)
{
printf(“%d “,xx[i]);
}
printf(“\n”);
return 0;
}
本题要求实现一个对整数数组进行简单排序的函数。
函数原型为:void sort( int a[], int n );
其中
a
是待排序的数组,
n
是数组
a
中元素的个数。该函数用某种方法将数组
a
中的元素按升序排列,结果仍然在数组
a
中。
#include<stdio.h>
int main()
{
int i, n;
scanf(“%d”, &n);
int a[n];
for (i = 0; i < n; i++)
scanf(“%d”, &a[i]);
sort(n,a);
printf(“After sorted the array is:”);
for (i = 0; i < n; i++)
printf(” %d”, a[i]);
printf(“\n”);
return 0;
}
void sort(int n, int a[n])
{
int i, j,temp;
for (i = 0; i < n; i++)
{
for (j = i; j < n; j++)
{
if (a[i] > a[j])
{
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
}
本题引用自PTA,原作者:浙江大学C课程组
本题要求实现一个求整数的逆序数的简单函数。
函数原型为:int reverse( int number );
其中函数
reverse
须返回用户传入的整型
number
的逆序数。
#include<stdio.h>
int main()
{
int n;
int reverse(int number);
scanf(“%d”, &n);
printf(“%d\n”, reverse(n));
return 0;
}
int reverse(int number)
{
int num=0,n,wei,len=0,temp=number;
int i, j;
while (temp != 0)
{
temp /= 10;
len += 1;
}
n = len;
for (i = 0; i < len; i++)
{
wei = number % 10;
num = num+wei * pow(10, n-1);
number /= 10;
n -= 1;
}
return num;
}
本题引用自PTA,原作者:山东理工大学巨同升
本题要求的程序功能是:首先在main函数中输入10个数,然后在被调函数ave中求出这10个数的平均值,最后在main函数中输出结果。要求写出函数ave。
函数原型为:double ave(double a[],int n);
其中
a
和
n
是由主调函数传入的参数。
#include<stdio.h>
int main(void)
{
int N;
double ave(double a[], int n);
scanf(“%d”, &N);
double x[N], p;
int i;
for (i = 0; i < N; i++)
scanf(“%lf”, &x[i]);
p = ave(x, N);
printf(“ave=%.2f\n”, p);
return 0;
}
double ave(double a[], int n)
{
double sum=0;
int i, j;
for (i = 0; i < n; i++)
{
sum = sum + a[i];
}
sum = sum / n;
return sum;
}
本题引用自PTA, 原作者:浙江大学张高燕
若两个复数分别为:c1=x1+y1i 和c2=x2+y2i,则它们的乘积为 c1×c2=(x1x2−y1y2)+(x1y2+x2y1)i。
本题要求实现一个函数计算两个复数之积。
函数原型为:
double result_real, result_imag; //这是两个全局变量void complex_prod( double x1, double y1, double x2, double y2 );
其中用户传入的参数为两个复数
x1
+
y1
i 和
x2
+
y2
i;函数
complex_prod
应将计算结果的实部存放在全局变量
result_real
中、虚部存放在全局变量
result_imag
中。
#include<stdio.h>
double result_real, result_imag;
int main(void)
{
double imag1, imag2, real1, real2;
void complex_prod(double x1, double y1, double x2, double y2);
scanf(“%lf %lf”, &real1, &imag1);
scanf(“%lf %lf”, &real2, &imag2);
complex_prod(real1, imag1, real2, imag2);
printf(“product of complex is (%f)+(%f)i\n”, result_real, result_imag);
return 0;
}
void complex_prod(double x1, double y1, double x2, double y2)
{
result_real = x1*x2-y1*y2;
result_imag = x1 * y2 + x2 * y1;
}
本题引用自PTA,原作者:浙大城市学院张高燕
本题要求实现一个函数,统计给定区间内的三位数中有两位数字相同的完全平方数(如144、676)的个数。
函数原型为:int search( int n );
其中传入的参数
int n
是一个三位数的正整数(最高位数字非0)。函数
search
返回[101,
n
]区间内所有满足条件的数的个数。
#include<stdio.h>
int main()
{
int number;
int search(int n);
scanf(“%d”, &number);
printf(“count=%d\n”, search(number));
return 0;
}
int search(int n)
{
int i, j=0;
int a,b,c,num;
for (i = 101; i < n; i++)
{
a = i % 10; b = (i / 10) % 10; c = (i / 100) % 10;
num = sqrt(i);
if (a == b || b == c || a == c)
if( i == num * num)
j ++;
}
return j;
}
本题要求实现求Fabonacci数列项的函数。Fabonacci数列的定义如下:
f(n)=f(n−2)+f(n−1) (n≥2),其中f(0)=0,f(1)=1。
函数原型如下:int f( int n );
函数
f
应返回第
n
个Fabonacci数。
#include<stdio.h>
int main()
{
int n;
int f(int n);
scanf(“%d”, &n);
printf(“%d\n”, f(n));
return 0;
}
int f(int n)
{
int i, j,num;
if (n == 1) { num = 1; return num; }
if (n == 2) {
num = 1; return num;
}
num = f(n – 1) + f(n – 2);
return num;
}
本题引用自PTA,原作者:浙江大学陈越
本题要求实现一个计算非负整数阶乘的简单函数。函数原型为:int Factorial( const int N );
其中
N
是用户传入的参数,其值不超过12。如果
N
是非负整数,则该函数必须返回
N
的阶乘,否则返回0。
#include<stdio.h>
int Factorial(int N);
int main()
{
int N, NF;
scanf(“%d”, &N);
NF = Factorial(N);
if (NF) printf(“%d! = %d\n”, N, NF);
else printf(“Invalid input\n”);
return 0;
}
int Factorial(int N)
{
int i,j,num = 1;
if (N > 0 && N <= 12)
{
for (i = 1; i <= N; i++)
{
num = num * i;
}
return num;
}
else { return 0; }
}
本题引用自PTA,原作者:浙江大学陈越
本题要求实现判断给定整数奇偶性的函数。函数原型为:
int even( int n );
其中
n
是用户传入的整型参数。当
n
为偶数时,函数返回1;
n
为奇数时返回0。注意:0是偶数。
#include<stdio.h>
int main()
{
int n;
int even(int n);
scanf(“%d”, &n);
if (even(n))
printf(“%d is even.\n”, n);
else
printf(“%d is odd.\n”, n);
return 0;
}
int even(int n)
{
if (n % 2 == 0)return 1;
else { return 0; }
}
编制程序,设计一个函数,这个函数用于判断一个字符串是否回文串。所谓回文串,是一个正读和反读都一样的字符串。例如”level”和”moom”
该函数的原型如下:
int isPalindromicString(char s[ ]);
这个函数接收要判断的字符串的首地址并判断其是否回文串。是则返回1,不是则返回0。
#include<stdio.h>
int main() {
char s[100];
int isPalindromicString(char s[]);
gets(s);
if (isPalindromicString(s))
printf(“Yes”);
else
printf(“No”);
return 0;
}
int isPalindromicString(char s[])
{
int len, i, j;
len = strlen(s);
if (len % 2 == 0)
{
for (i = 0; i < len / 2; i++)
{
if (s[i] != s[len – i-1])return 0;
else { return 1; }
}
}
if (len % 2 != 0)
{
for (i = 0; i < (len – 1) / 2; i++)
{
if (s[i] != s[len – i-1])return 0;
else { return 1; }
}
}
}
给定正整数N,函数F(N)表示小于等于N的自然数中1和2的个数之和,例如:1,2,3,4,5,6,7,8,9,10序列中1和2的个数之和为3,因此 F(10)=3。输入N,求F(N)的值,1=<N<=10^100(10的100次方)若F(N)很大,则求F(N)mod20123的值
#include<stdio.h>
int main() {
int i, j, n;
int F(int n);
while(scanf(“%d”,&n)!=EOF)
{
printf(“%d\n”, F(n));
}
}
int F(int n)
{
int i,k, len=0,temp=n,j=0,a;
for (i = 1; i <= n; i++)
{
while (temp != 0)
{
temp /= 10;
len += 1;
}
int itemp = i;
for (k = 0; k < len; k++)
{
a = itemp % 10;
itemp /= 10;
if (a == 1 || a == 2)
j++;
}
}
return j;
}
在算法4-1中已经描述过一种定位子串的算法,但其依赖字符串的其他操作(使用了算法4-3描述的子串提取以及字符串比较)。
下面给出书中另一种相对独立的定位子串算法:

图:求子串位置的定位函数
书中的算法思想是这样的:分别利用计数指针i和j指示主串S和模式串T中当前正待比较的字符位置。算法的基本思想是:从主串S的第pos个字符起和模式的第一个字符比较之,若相等,则继续逐个比较后续字符,否则从主串的下一个字符起再重新和模式的字符比较之。依次类推,直至模式T中的每个字符依次和主串S中的一个连续的字符序列相等,则称匹配成功,函数值为和模式T中第一个字符相等的字符在主串中的序号,否则称匹配不成功,函数值为零。
你的任务是将S中每次比较的字符输出来,并将匹配的序号输出。
#include<stdio.h>
typedef struct
{
char s[1000];
int len;
}SString;
int Index(SString S, SString T)
{
int pos = 0;
int i = 0, j = 0;
while (i < S.len && j < T.len)
{
if (S.s[i] == T.s[j])
{
printf(“%c”, S.s[i]);
++i; ++j;
}
else
{
printf(“%c”, S.s[i]);
j = 0;
i = ++pos;
}
}
putchar(‘\n’);
if (j == T.len)
return pos;
else
return -1;
}
int main()
{
SString S, T;
int pos;
int n, m, j, k, i;
while (~scanf(“%s”, S.s))
{
scanf(“%s”, T.s);
S.len = strlen(S.s);
T.len = strlen(T.s);
int ans = Index(S, T) + 1;
printf(“%d\n”, ans);
}
return 0;
}
本题目要求计算下列分段函数f(x)的值:
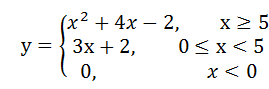
#include<stdio.h>
int main()
{
double answer(double x);
double x, y;
scanf(“%lf”, &x);
printf(“f(%.1lf) = %.1lf”,x, answer(x));
}
double answer(double x)
{
double y, i, j;
if (x >= 5)
{
y = x * x + 4 * x – 2;
return y;
}
else if (0 <= x && x < 5)
{
y = 3 * x + 2; return y;
}
else if (x < 0)
return 0.0;
}