贪心&动态规划&回溯&分支限界，四种算法解决01背包问题，有流程图和总结

01背包问题

直接copy就能当实验报告…

问题说明

	01背包是在M件物品取出若干件放在空间为W的背包里，每件物品的体积为W1，W2至Wn，与之相对应的价值为P1,P2至Pn。采取怎样的策略能使装入背包的价值最大。

贪心算法

算法思路

计算商品的单位质量价值，并对其进行排序，在不超过背包容量的情况下，选取单位质量价值从高往低装载

流程图

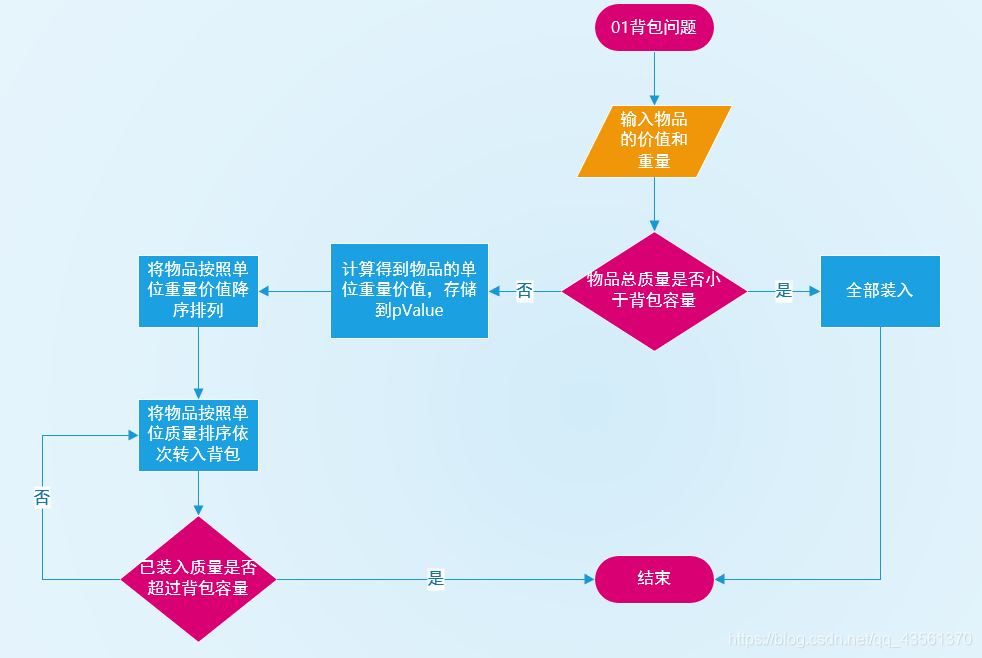
在这里插入图片描述

算法实现

class Pack:

    def __init__(self, value,  weight):
        self.value = value
        self.weight = weight
        self.pValue = value/weight

def greed(goods, maxLoad):

    goods.sort(key=lambda x: x.pValue, reverse = True)

    load = 0
    tValue = 0
    loaded = []

    for each in goods:
        if load < maxLoad:
            tValue += each.value
            load += each.weight
            loaded.append(each)

    return tValue, loaded

if __name__ == '__main__':
    n, m= [int(n) for n in input("背包数量和最大承载：").split()]

    goods = []
    while n > 0:
        num = [int(n) for n in input().split()]
        good = Pack(num[0], num[1])
        goods.append(good)
        n -= 1

    total, loaded = greed(goods, m)

    print("total:", total)
    for v in loaded:
        print(v.value)

运行样例

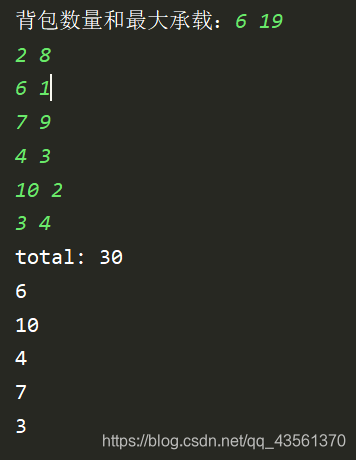
在这里插入图片描述

算法总结

贪心算法往往只能得到问题的局部最优解，最后给出较为接近计算精度要求的最优解。但对诸如最短路径问题、最小生成树问题、哈夫曼编码问题等具有最优子结构和贪心选择性质的问题却可以获得整体最优解。

贪心算法以其简洁、直观著称，对于求解精度要求不很高的问题有着重要意义。

动态规划算法

算法思路

动态规划算法是将原问题分解为一个个子问题，寻找子问题的最优解，构成员问题的最优解。这是一种自底向上求解算法。使用动态规划的前提是能够找到最优子结构。将最优的子结构存储起来，完成自下而上的递推求解。

对于
table[i][j]
，其表示的是前i件物品放入一个容量为
j
的背包中，可以获得的最大价值。在得到前
i-1
件商品放入与否的最优解后，进而求解第
i
件物品的放入与否。

不放入第
i
件物品，x
_i
= 0，背包中的物品总价值不变，那么原问题可化为“前i-1件物品放入容量为j的背包中”，最大价值为
table[i-1][j]
放入第
i
件物品，x
_i
= 1，背包的总价值增加
v[i]
，此时问题转化为前
i-1
件物品的最大价值
table[i-1][j-w[i]]
再加上
v[i]
的价值
- 而此时就会有背包的容量是否能装下第
  i
  件物品的空间的问题
a

b

l

e

[

i

]

[

j

]

=

{

t

a

b

l

e

[

i

−

1

]

[

j

]

,

w

h

e

n

j

<

w

i

m

a

x

(

t

a

b

l

e

[

i

−

1

]

[

j

]

,

t

a

b

l

e

[

i

−

1

]

[

j

−

w

[

i

]

]

+

v

[

i

]

)

,

w

h

e

n

j

≥

w

i

table[i][j] = \begin{cases} table[i-1][j],\quad when\ j < w_i \\ max(table[i-1][j], table[i-1][j-w[i]] + v[i]), \quad when\ j \geq w_i \end{cases}

$t a b l e [i] [j] = {t a b l e [i - 1] [j], w h e n j < w_{i} m a x (t a b l e [i - 1] [j], t a b l e [i - 1] [j - w [i]] + v [i]), w h e n j \geq w_{i}$

复杂度

n
²

流程图

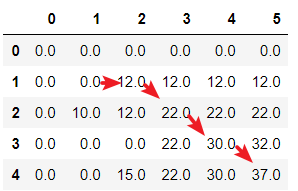
在这里插入图片描述

在实现本题算法执之前，我多次尝试该类动态规划表的填写，并逐渐理解其中的原理

算法实现

import numpy as np

if __name__ == '__main__':
    W = 5
    value = [0, 12, 10, 20, 15]
    weight = [0, 2, 1, 3, 2]
    table = np.zeros((5, W+1))

    for i in range(1, 5):
        for j in range(1, 6):
            if((j-weight[i]) < 0):
                continue
            table[i][j] = max(table[i-1][j-weight[i]] + value[i], table[i-1][j])

    print(table[4, 5])

运行样例

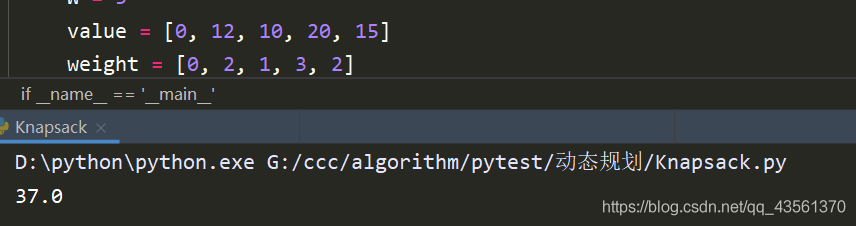
在这里插入图片描述

算法总结

一般来说动态规划算法只要设计得当，效率往往是很高的，在时间上溢出的可能性不大，但是由于动态规划需要记录大量的中间过程，对内存空间的需求较大，设计不合理很有可能导致内存的溢出。

动态规划广泛地运用于生物信息学中，诸如序列比对，蛋白质折叠，RNA结构预测和蛋白质-DNA结合等任务。

回溯法

算法思想

01
背包需要用回溯法构造解的子集树。对于每一个物品i，对于该物品只有选与不选2个决策，总共有n个物品，可以顺序依次考虑每个物品，这样就形成了一棵解空间树。

基本思想就是遍历这棵树，以枚举所有情况。对于在该子集树中每个节点处进行选与不选的决策，如果剩余空间能容下当前物品则将其装入，并搜索左子树；如果不装入当前物品，且满足限界条件（剩余物品价值与当前价值的总和大于最优解）就搜索其右子树。

这里左右子树并不冲突，只是当且仅当满足约束条件时才可以装入，而不管是否满足约束条件都会进行限界条件的判断。

流程图

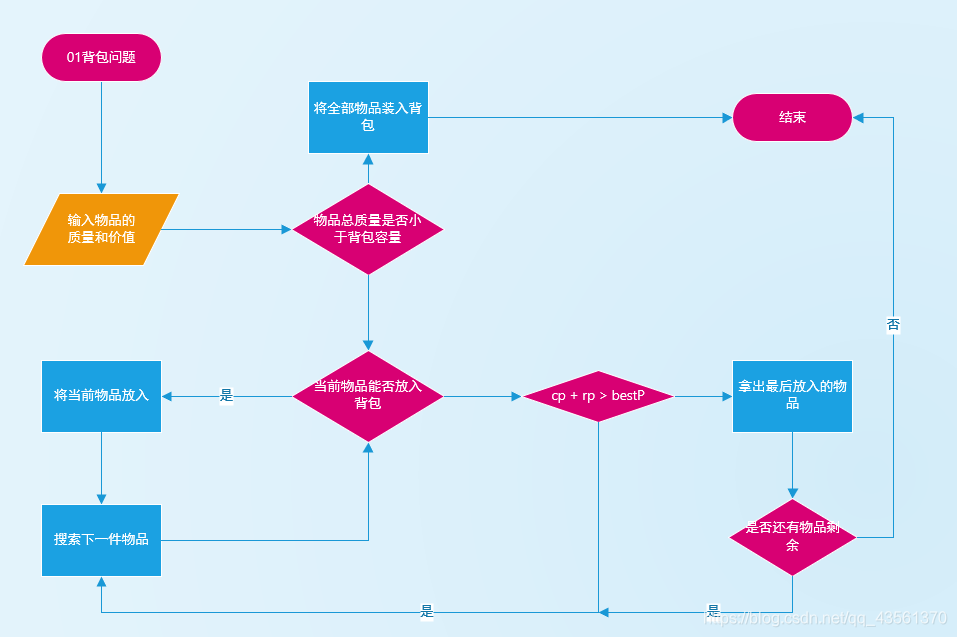
在这里插入图片描述

算法实现

import numpy as np

weight = [0, 2, 5, 4, 2]
value = [0, 6, 3, 5, 4]
flag = np.full(len(value), False)
W = 10
bestV = 0
bestX = flag
cv = 0
cw = 0

def back(k):
    global maxV, cv, cw, bestV

    if k >= len(value):
        if cv > bestV:
            for i in range(1, len(value)):
                bestX[i] = flag[i]

            bestV = cv

            return

    if cw + weight[k] <= W:    #判断左子树是否符合条件
        flag[k] = True
        cw += weight[k]
        cv += value[k]
        back(k+1)
        cv -= value[k]
        cw -= weight[k]

    if (bound(k+1, cv) > bestV):   #右子树
        flag[k] = False
        back(k+1)


def bound(k, cv):
    rv = 0

    while(k < len(value)):
        rv += value[k]
        k += 1

    return cv + rv

if __name__ == '__main__':
    back(1)
    print(bestV)

运行样例

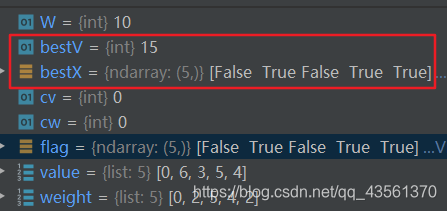
在这里插入图片描述

算法总结

回溯法从本质上看，就是一种深度优先搜索的试探算法，寻找最优或者符合条件的解。

回溯法和穷举法有些类似，它们都是基于试探的。区别时穷举法需要将一个解的各个部分全部生成后才检查是否满足条件，不满足则完全放弃该解进而尝试其他的解。这时回溯法的好处就体现出来了，它的解时一步步生成的，在当前解不满足条件时会回退一步去求解，而且回溯法对解空间进行了限界对于结果是否符合条件进行预判，降低时间成本。

分支限界法（FIFO)

算法思想

物品放入背包中或物品不放入背包中，根据约束条件舍去无效情况。当前物品k放入背包中时，获取当前最大总价值，下一个物品k+1也存在放入背包和不放入背包中两个节点。当物品k不放入背包时，上个节点的最总价值为当前节点的最总价值，下一个物品k+1仍然存在放入背包和不放入背包两个节点。对于物品k+1以此类推，最终根据不同的放入情况选择一个最优解作为可以放入背包物品的最大总价值。

该算法为队列法分支限界法。

算法模拟

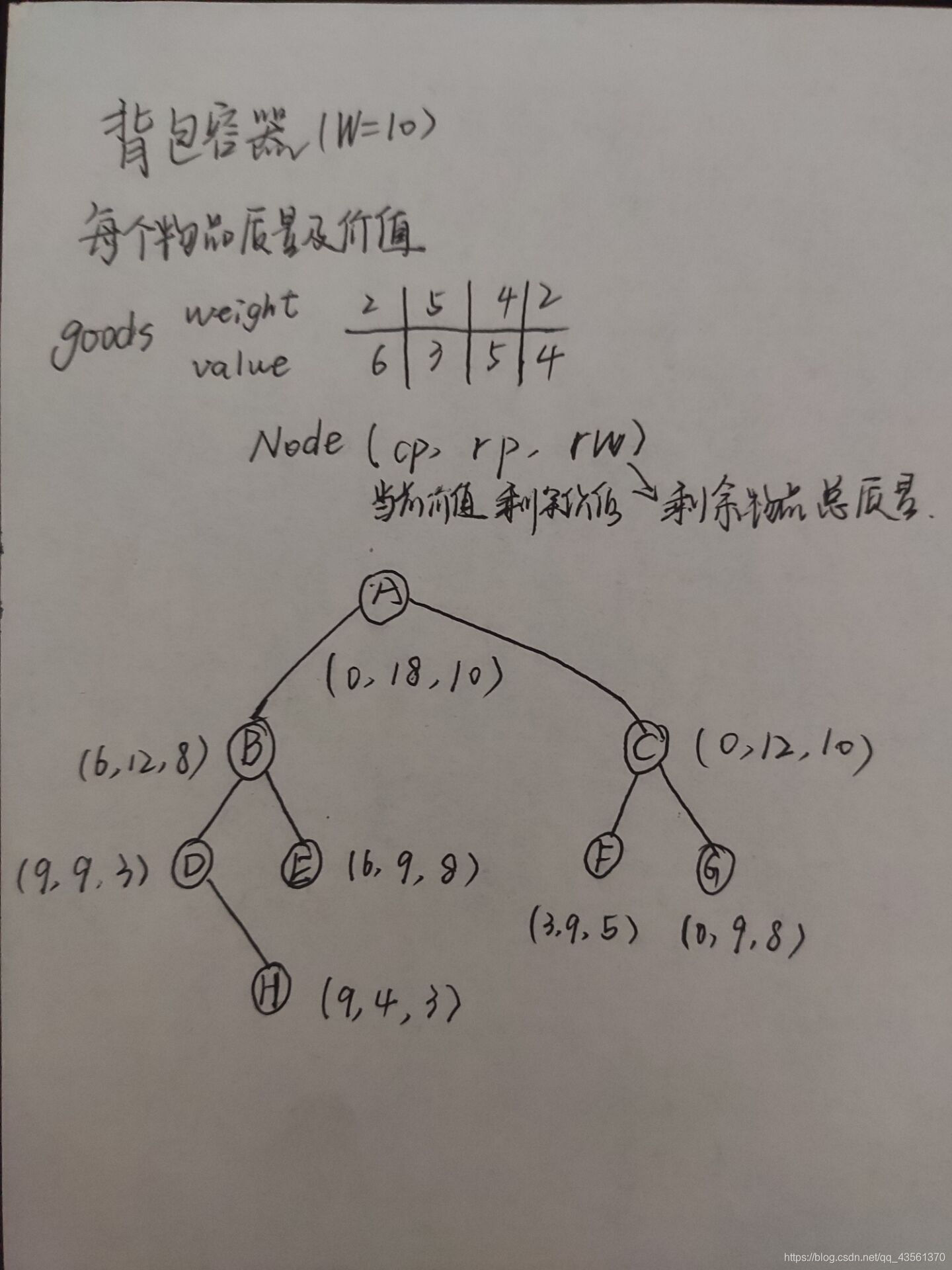
在这里插入图片描述

第一次实验时，对回溯法和分支限界法较为生疏，所以在纸上对其进行了多次模拟，并经过调试最终写出了算法。

算法实现

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class ZeroAndOne {
    static int N = 10;
    static Goods[] goods = new Goods[N];
    static boolean[] bestX = new boolean[N];
    static int bestP, W, n, sumW, sumV; //bestP最优值，W为容量， n为物品数
                                        //sumW所有物品的总重量，sumV总价值

    public static void main(String[] args) {

        Scanner scanner = new Scanner(System.in);
        System.out.print("n:");
        n = scanner.nextInt();
        System.out.print("W:");
        W = scanner.nextInt();
        bestP = 0;
        sumW = 0;
        sumV = 0;

        System.out.printf("w, v:");
        for (int i = 1; i <= n; i++) {

            int weight = scanner.nextInt();
            int value = scanner.nextInt();
            Goods good = new Goods(weight, value);
            goods[i] = good;

            sumW += goods[i].weight;
            sumV += goods[i].value;
        }

        if (sumW <= W) {
            bestP = sumV;
            System.out.println("全放，价值：" + bestP);
        } else {
            bfs();
            System.out.println("bestP:" + bestP);

            System.out.println("these:");
            for (int i = 1; i <= n; i++) {
                if (bestX[i]) {
                    System.out.print(i + " ");
                }
            }
        }
    }

    static class Node {
        int cp;      //当前总价值
        int rp;      //剩余物品的总价值
        int rw;      //背包剩余容量
        int id;      //物品号

        boolean []x = new boolean[N];

        public Node(int cp, int rp, int rw, int id) {
            this.cp = cp;
            this.rp = rp;
            this.rw = rw;
            this.id = id;
        }
    }

    static class Goods {

        int weight;
        int value;

        public Goods(int weight, int value) {
            this.weight = weight;
            this.value = value;
        }
    }

    public static int bfs() {

        int t, tcp, trp, trw;
        /**
         * t 当前物品序号
         * tcp 当前cp trp  trw同
         */

        Queue<Node> myQueue=new LinkedList<>();
        myQueue.add(new Node(0, sumV, W, 1));


        while (!myQueue.isEmpty()) {

            Node liveNode = new Node(0, 0, 0, 0);
            Node lChild = new Node(0, 0, 0, 0);
            Node rChild = new Node(0, 0, 0, 0);

            liveNode = myQueue.poll();
            t = liveNode.id;

            //如果为最后一个节点就不再搜索，没有剩余容量也不再搜索
            if (t > n || liveNode.rw == 0) {

                if (liveNode.cp >= bestP) {
                    for (int i = 1; i <= n; i++) {
                        bestX[i] = liveNode.x[i];
                    }

                    bestP = liveNode.cp;
                }

                continue;
            }

            //不满足条件不再搜索
            if (liveNode.cp + liveNode.rp < bestP) {
                continue;
            }

            tcp = liveNode.cp;
            trp = liveNode.rp - goods[t].value;   //不管当前商品是否装入，剩余价值都会减少
            trw = liveNode.rw;

            //满足约束条件,放入背包
            if (trw >= goods[t].weight) {

                lChild.rw = trw - goods[t].weight;
                lChild.cp = tcp + goods[t].value;
                lChild = new Node(lChild.cp, trp, lChild.rw, t+1);

                for (int i = 1; i < t; i++) {
                    lChild.x[i] = liveNode.x[i];
                }

                lChild.x[t] = true;
                if (lChild.cp > bestP) {
                    bestP = lChild.cp;
                }

                myQueue.add(lChild);
            }

            //右孩子
            if (tcp + trp >= bestP) {
                rChild = new  Node(tcp, trp, trw, t+1);

                for (int i =1; i < t; i++) {
                    rChild.x[i] = liveNode.x[i];
                }
                rChild.x[t] = false;
                myQueue.add(rChild);
            }
        }

        return bestP;
    }
}

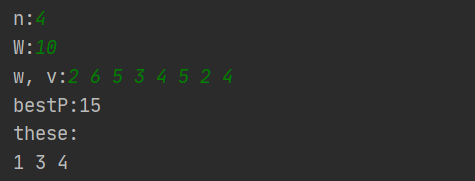
运行样例

回溯与分支限界

共同点：一种在问题的解空间树上搜索问题解的算法。

运行样例

在这里插入图片描述

回溯与分支限界

共同点：一种在问题的解空间树上搜索问题解的算法。
不同点：求解目标不同，回溯法的目标是找出解空间树满足约束条件的所有解，而分支限界法的求解目标是尽快地找出满足约束条件的一个解；搜索方法不同，回溯法采用深度优先方法搜索解空间，而分支限界法一般采用广度优先或以最小消耗优先的方式搜索解空间树；对扩展结点的扩展方式不同，回溯法中，如果当前的扩展结点不能够再向纵深方向移动，则当前扩展结点就成为死结点，此时应回溯到最近一个活结点处，并使此活结点成为扩展结点。分支限界法中，每一次活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点；存储空间的要求不同，分支限界法的存储空间比回溯法大得多，当内存容量有限时，回溯法成功的可能性更大。

原文链接：https://blog.csdn.net/qq_43561370/article/details/108210766

01背包问题

问题说明

贪心算法

算法思路

流程图

算法实现

运行样例

算法总结

动态规划算法

算法思路

流程图

算法实现

运行样例

算法总结

回溯法

算法思想

流程图

算法实现

运行样例

算法总结

分支限界法（FIFO)

算法思想

算法模拟

算法实现

运行样例

回溯与分支限界

运行样例

回溯与分支限界

你可能也喜欢