博客

题目描述：

用1 x 2的多米诺骨牌填满M x N的矩形有多少种方案，M<=5，N<2^31，输出答案mod p的结果

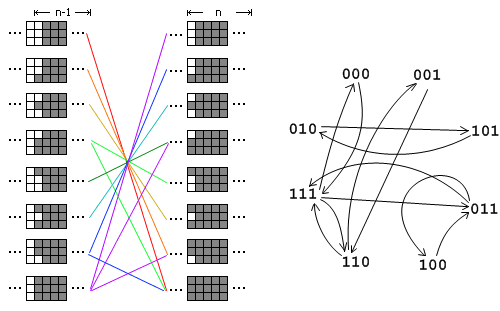
矩阵乘法：

#include <iostream>     
#include <algorithm>
#include <functional>
using namespace std;    

#define SIZE (1<<m)
#define MAX_SIZE 32

class CMatrix
{
    public:
        long element[MAX_SIZE][MAX_SIZE];
        void setSize(int);
        void setModulo(int);
        CMatrix operator* (CMatrix);
        CMatrix power(int);
    private:
        int size;
        long modulo;
};

void CMatrix::setSize(int a)
{
    for (int i=0; i<a; i++)
        for (int j=0; j<a; j++)
            element[i][j]=0;
    size = a;
}

void CMatrix::setModulo(int a)
{
    modulo = a;
}

CMatrix CMatrix::operator* (CMatrix param)
{
    CMatrix product;
    product.setSize(size);
    product.setModulo(modulo);
    for (int i=0; i<size; i++)
        for (int j=0; j<size; j++)
            for (int k=0; k<size; k++)
            {
                product.element[i][j]+=element[i][k]*param.element[k][j];
                product.element[i][j]%=modulo;
            }

    return product;
}

CMatrix CMatrix::power(int exp)
{
    CMatrix tmp = (*this) * (*this);
    if (exp==1) return *this;
    else if (exp & 1) return tmp.power(exp/2) * (*this);
    else return tmp.power(exp/2);
}


int main()
{
    const int validSet[]={0,3,6,12,15,24,27,30};
    long n, m, p;
    CMatrix unit;
    
    n=1024;
	m=3;
	p=999999;

    unit.setSize(SIZE);
    for(int i=0; i<SIZE; i++)
        for(int j=0; j<SIZE; j++)
            if( ((~i)&j) == ((~i)&(SIZE-1)) )
            {
                bool isValid=false;
                for (int k=0; k<8; k++)isValid=isValid||(i&j)==validSet[k];
                unit.element[i][j]=isValid;
            }

    unit.setModulo(p);
    printf("%d", unit.power(n).element[SIZE-1][SIZE-1] );
    return 0;
}