文章目录

前言
一、数据模型
二、关系数据模型
三、关系
总结

前言

本文主要讲解了关系型数据库的相关知识，涉及关系数据模型和关系的知识

一、数据模型

1.什么是数据模型

数据模型是一组集成的概念，用于

描述和操作组织内的数据、数据间的联系，以及对数据的约束。

数据模型是数据库系统的核心和基础

。各种机器上实现的DBMS软件都是基于某种数据模型

2.数据模型的基本要素

数据结构是对系统静态特征的描述，数据操作是对系统动态特性的描述。

（1）数据结构

数据结构

是：

1.与数据类型、内容、性质有关的对象，如网状模型中的数据项、记录，关系模型中的域、属性、关系等

2.与数据之间联系有关的对象，如网状模型中的系型（Set Type）

（2）数据操作

数据操作

是

指对数据库中各种对象的实例允许执行的操作的集合，包括操作及有关的操作规则

数据库主要有

检索和更新

两大类操作。

（3）数据的约束条件

数据的约束条件

是

一组完整性规则的集合

数据模型应该反映和规定本

数据模型必须遵守的基本的通用的完整性约束条件

。此外，数据模型还应提供定义完整性约束条件的机制，以反映具体应用所涉及的

数据必须遵守的特定的语义约束条件

二、关系数据模型

1.关系数据模型的基本概念

（1）关系实例

关系实例是由命名的若干列和行组成的表格。

要强调的是：

一般情况下，关系指代实例。

（2）关系模式

关系模式是对关系的描述。关系模式通常可以简记为:

(

)

或

(

，

…

，

）

R (U) 或 R (A1，A2，…，An）

$R (U) 或 R (A 1 ， A 2 ， \dots ， A n ）$

关系模式可以形式化地表示为：

（

，

）

R（U，D，dom，F）

$R （ U ， D ， d o m ， F ）$

R     关系名
U     组成该关系的属性名集合
D     属性组U中属性所来自的域
dom   属性向域的映象集合,常常直接说明为属性的类型、长度
F     属性间的数据依赖关系集合

(3)关系数据库

在一个给定的应用领域中，所有

实体及实体之间联系的关系的集合

构成一个关系数据库。

因为关系由两部分组成，所以关系数据库也是由两部分组成，即

关系模式的集合

及

对应的关系实例的集合

。

关系模式的集合称为数据库模式，对应的关系实例的集合称为数据库实例。

2.关系数据模型的数据结构

（1）元组

表中的

一行，表示一个实体

，关系是由元组组成的。

（2）属性

表中的

每一列在关系中称为属性

，每个属性都有一个属性名，属性值则是各元组属性的取值。

（3）域

属性的取值范围

称为域。同一属性只能在相同域中取值。

（4）分量

元组中的一个

属性值

。

例子1：

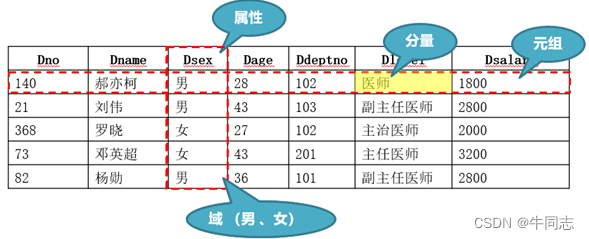
在这里插入图片描述

（5）键

关系中能

唯一区分不同元组的

属性

或

属性组合

，称为关系的一个键，或者称为关键字、码。关键字的属性值

不能取“空值”。

（6）候选键

关系中能够成为关键字的属性或属性组合可能不是唯一的。

凡在关系中能够唯一区分确定不同元组的属性或属性组合，称为候选健。

其中：

包括在候选键中的属性称为

主属性

，不包括在候选键中的属性称为

非主属性

。

（7）主键

当一个关系中有多个候选健的时候，则从中选定一个作为关系的主键

关系中主键是唯一的。每个关系中有且只有一个主键。

（8）外键

关系中某个属性或属性组合并

非该关系的键，但却是另一个关系的主键

，称此属性或属性组合组合为

本关系的外键

。

例子2

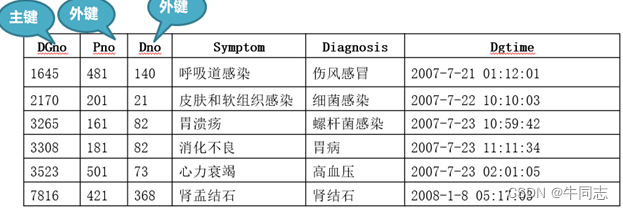
在这里插入图片描述

3.关系数据模型的数据操作

关系模型中常用的关系操作包括两类：

1.检索（查询）
2.更新（插入、删除和修改）

用户可以通过关系语言来完成对数据的各种操作。

可用讲关系语言理解为一个个库函数，或者是命令行的指令

4.关系数据模型的数据约束

分为三大类：

1.数据模型中固有的约束
2.可以在数据模型的模式中直接表述的约束 
3.不能在数据模型的模式中直接表述的约束

5.关系数据模型的优缺点

（1）优点

1.关系模型与非关系模型不同，它是建立在严格的数学概念的基础上的。

2.数据结构简单、清晰。

3.更高的数据独立性，更好的安全保密性。

4.丰富的完整性。

（2）缺点

1.对“现实世界”实体的表达能力弱。

2.

由于存取路径对用户透明

（即用户无法直接获取存取路径），查询效率往往不如非关系数据模型。

3.关系模型只有一些固定的操作集。

4.不能很好的支持业务规则。

三、关系

1.域、笛卡尔积和关系

（1）域

域是一组

具有相同数据类型的值

的集合。

例如：

1. 自然数、整数、实数
2. 长度小于25字节的字符串
3. 指定长度的字符串的集合
4. {‘男’，‘女’}

（2）笛卡尔积

基数

(

＝

…

)

为有限集，其基数为

＝

…

)

则

…

的基数

为：

若D_i(i＝1,2,…,n)为有限集，其基数为m_i,i＝1,2,…,n),则D_1\times D_2\times …\times D_n的基数M为：

$若 D_{i} (i ＝ 1, 2, \dots, n) 为有限集，其基数为 m_{i}, i ＝ 1, 2, \dots, n), 则 D_{1} \times D_{2} \times \dots \times D_{n} 的基数 M 为：$

∏

M=\prod_{i=1}^{n}m_i

$M = i = 1 \prod n m_{i}$

笛卡儿积

，

…

，

，允许其中某些域是相同的。

给定一组域D_1，D_2，…，D_n，允许其中某些域是相同的。

$给定一组域 D_{1} ， D_{2} ， \dots ， D_{n} ，允许其中某些域是相同的。$

那么:

，

…

，

的笛卡尔积为

D_1，D_2，…，D_n的笛卡尔积为

$D_{1} ， D_{2} ， \dots ， D_{n} 的笛卡尔积为$

：

…

＝

{

(

…

)

∣

∈

＝

…

}

D_1\times D_2\times …\times D_n ＝\{(d_1,d_2,…,d_n)|d_i\in D_i,i＝1,2,…,n\}

$D_{1} \times D_{2} \times \dots \times D_{n} ＝ {(d_{1}, d_{2}, \dots, d_{n}) ∣ d_{i} \in D_{i}, i ＝ 1, 2, \dots, n}$

其中每一个元素

…

)

(d_1,d_2,…,d_n )

$(d_{1}, d_{2}, \dots, d_{n})$

叫作一个

n元组

，元组中每一个值

d_i

$d_{i}$

叫做一个

分量

。

笛卡儿积是所有域的所有取值的一个集合，分量不能重复

笛卡尔积可表示为一张二维表，表中的每行对应一个元组，表中的每列对应一个域

例子

例如，给出3个域：

导师集合

{

张清玫，刘逸

}

专业集合

{

计算机专业，信息专业

}

研究生集合

{

李勇，刘晨，王敏

}

D_1=导师集合SUPERVISOR=\{张清玫，刘逸\}\\ D_2=专业集合SPECIALITY=\{计算机专业，信息专业\}\\ D_3=研究生集合POSTGRADUATE=\{李勇，刘晨，王敏\}

$D_{1} = 导师集合 S U PER V I SOR = {张清玫，刘逸} D_{2} = 专业集合 SPEC I A L I T Y = {计算机专业，信息专业} D_{3} = 研究生集合 POSTGR A D U A TE = {李勇，刘晨，王敏}$

D_1,D_2,D_3

$D_{1}, D_{2}, D_{3}$

的

笛卡尔积为

:

＝

{

(

张清玫，计算机专业，李勇

)

(

张清玫，计算机专业，刘晨

)

(

张清玫，计算机专业，王敏

)

(

张清玫，信息专业，李勇

)

(

张清玫，信息专业，刘晨

)

(

张清玫，信息专业，王敏

)

(

刘逸，计算机专业，李勇

)

(

刘逸，计算机专业，刘晨

)

(

刘逸，计算机专业，王敏

)

(

刘逸，信息专业，李勇

)

(

刘逸，信息专业，刘晨

)

(

刘逸，信息专业，王敏

)

}

D=D_1\times D_2\times D_3＝\\ \{ (张清玫，计算机专业，李勇),\\(张清玫，计算机专业，刘晨),\\ (张清玫，计算机专业，王敏),\\(张清玫，信息专业，李勇),\\ (张清玫，信息专业，刘晨),\\(张清玫，信息专业，王敏),\\ (刘逸，计算机专业，李勇),\\(刘逸，计算机专业，刘晨),\\ (刘逸，计算机专业，王敏),\\((刘逸，信息专业，李勇),\\( (刘逸，信息专业，刘晨),\\((刘逸，信息专业，王敏) \}

$D = D_{1} \times D_{2} \times D_{3} ＝ {(张清玫，计算机专业，李勇), (张清玫，计算机专业，刘晨), (张清玫，计算机专业，王敏), (张清玫，信息专业，李勇), (张清玫，信息专业，刘晨), (张清玫，信息专业，王敏), (刘逸，计算机专业，李勇), (刘逸，计算机专业，刘晨), (刘逸，计算机专业，王敏), ((刘逸，信息专业，李勇), ((刘逸，信息专业，刘晨), ((刘逸，信息专业，王敏)}$

基数为

｜

＝

｜D_1｜\times｜D_2｜\times｜D_3｜= 2\times2\times3＝12

$｜ D_{1} ｜ \times ｜ D_{2} ｜ \times ｜ D_{3} ｜ = 2 \times 2 \times 3 ＝ 12$

转换成表为:

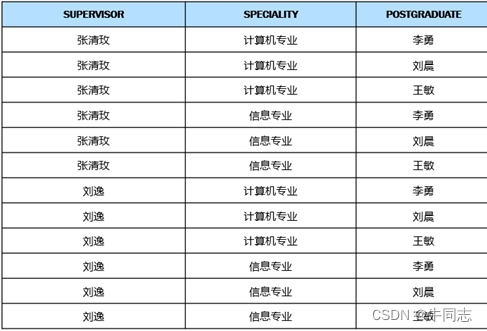
在这里插入图片描述

（3）关系

…

的子集叫作在域

…

上的关系

D_1×D_2×…×D_n的子集叫作在域D_1,D_2,…,D_n上的关系

$D_{1} \times D_{2} \times \dots \times D_{n} 的子集叫作在域 D_{1}, D_{2}, \dots, D_{n} 上的关系$

，表示为:

（

…

）

R（D_1,D_2,…,D_n）

$R （ D_{1}, D_{2}, \dots, D_{n} ）$

R：关系名

n：关系的目或者度（Degree）

关系中的每个元素是关系中的元组，通常用t表示。

单元关系与二元关系

当n=1时，

称该关系为单元关系（Unary relation），或者一元关系

当n=2时，

称该关系为二元关系（Binary relation）

关系的表示

关系也是一个二维表，

表的每行对应一个元组，表的每列对应一个域

2.关系的性质

一个关系通常有如下性质：

1.有一个关系名，并且跟关系模式中所有其他关系不重名
2.每一个单元格都包含且仅包含一个原子值（1NF）
3.每个属性都有一个不同的名字
4.同一属性中的各个值都取自相同的域
5.各个元组互不相同，不存在重复元组
6.属性的顺序并不重要
7.理论上讲，元组的顺序并不重要

3.关系模式和关系的区别

关系模式：

是型
对关系的描述
静态的、稳定的

关系：

是值
关系模式在某一时刻的状态或内容
动态的、随时间不断变化的

4.关系数据库模式

关系数据库模式S包含关系模式的集合

{

…

}

S=\{ R_1,R_2,…,R_m\}

$S = {R_{1}, R_{2}, \dots, R_{m}}$

和完整性约束的集合IC。

下表显示了一个关系数据库模式，记做HIS={Dept,Doctor,Patient,Diagnosis}。

在这里插入图片描述

5.关系数据库相关

（1）关系数据库的型和值

关系数据库的型：关系数据库模式，是对关系数据库的描述

关系数据库的值：关系模式在某一时刻对应的关系的集合，通常称为关系数据库

（2）关系数据库的物理组织

有的关系数据库管理系统中一个表对应一个操作系统文件，将物理数据组织交给操作系统完成

有的关系数据库管理系统从操作系统那里申请若干个大的文件，自己划分文件空间，组织表、索引等存储结构，并进行存储管理

6.关系完整性

（1）空

1.

代表当前不知道或是对这个元组不可用的一个属性值

。

2.空是处理不完整或异常数据的一种方法。

3.

空并不等于零值或空格所组成的字符串。

（2）实体完整性规则

规则如下：

1. 实体完整性规则是针对基本关系而言的。一个基本表通常对应现实世界的一个实体集。
2. 现实世界中的实体是可区分的，即它们具有某种唯一性标识。
3. 关系模型中以主码作为唯一性标识。
4. 主码中的属性即主属性不能取空值

（3）关系间的引用

在关系模型中实体及实体间的联系都是用关系来描述的，因此可能存在着关系与关系间的引用。

例如：

学生（

学号

，姓名，性别，专业号，年龄）

课程（

课程号

，课程名，学分）

选修（

学号

，

课程号

，成绩）

（4）外键

设F是基本关系R的一个或一组属性，但不是关系R的码。如果F与基本关系S的主码Ks相对应，则称F是R的外码

基本关系R称为

参照关系

（Referencing Relation）

基本关系S称为

被参照关系

（Referenced Relation）或

目标关系

（Target Relation）

（5）参照完整性规则

若属性（或属性组）F是

基本关系R的外码

它与

基本关系S的主码Ks

相对应（基本关系R和S不一定是不同的关系），则对于R中每个元组在F上的值必须为：

或者取空值（ F的每个属性值均为空值）

或者等于S中某个元组的主码值。

（6）用户自定义完整性

用户定义的完整性是针对某一具体关系数据库的约束条件，反映某一具体应用所涉及的数据必须满足的语义要求。

关系模型应提供定义和检验这类完整性的机制，以便用统一的系统的方法处理它们，而不要由应用程序承担这一功能

总结

文章的不妥之处请读者包涵与指正

原文链接：https://blog.csdn.net/weixin_52042488/article/details/126922465