流程:
一、平稳性分析 参考:
时间序列的平稳性检验方法(汇总篇) – 知乎 (zhihu.com)
二、白噪声分析 参考:
(74条消息) matlab5.白噪声检验_海滩超人的博客-CSDN博客_matlab白噪声序列检测
三、时序模型建立
模型识别-参数设置-白噪声检验-通过后模型建立完成
四、结果分析
前处理:
数据归一化:
pac_=mapminmax(pac,0,1);%注意pac数据应该为行数据,如果是对一列数据进行归一化,需要先转置
一、平稳性分析
平稳序列存在稳定的变化规律,因此时序分析需要数据是平稳的,以便捕获的规律能用于预测。
1、图形分析方法:
1)可视化数据
t=(1:3805); %根据序列数据个数赋值
plot(t,pac); %pac是检验的数据序列关于图象的美化,点击链接:
2)可视化统计特征
绘制自相关图和偏自相关图
(1)自相关图:
autocorr(qt_noGh_(:,5));判断依据:数据从1开始下降很慢为非平稳序列
非平稳序列转化为平稳序列(Matlab):
(73条消息) 时间序列平稳化的 8 种方法比较及Matlab实现_时间序列分析及应用周永道_图灵猫的博客-CSDN博客
%% 线型拟合平稳化
pac_pw = trend_fitting(pac_');%函数由链接获得
%% 多项式拟合平稳化
pac_dx6pw_ = polynomial_fitting(pac_pw,6);%函数由链接获得
%% 差分平稳化
pac_cf2pw_= difference(pac_',2);%函数由链接获得平稳序列的自相关系数会很快将为0。
(2)偏自相关图:
parcorr(qt_noGh_(:,5));判断依据:自相关系数下降很慢的非平稳序列,通常在Lag较小时,偏自相关系数较大,证明数据只与前一项有关。
2、简单统计方法
将数据前后拆分为两个序列,分别计算均值和方差,前后对比,无较大差异则无异常,有较大差异为异常或突变。
%% 求均值和均方差
pac_q=pac_y(1:1902);
pac_h=pac_y(1903:end); %取前半段和后半段
q=mean(pac_q);
h=mean(pac_h);%分别计算均值
plot(t,pac_y);
hold on
plot([0,1902],[q,q]);
hold on
plot([1903,3805],[h,h]);%画出前半段和后半段的均值线
%z=mean(pac_y)
%hold on
%plot([0,3805],[z,z]); %画全部的均值线
q_var=var(pac_q)
h_var=var(pac_h)
hold on
plot([0,1902],[q_var,q_var]);
hold on
plot([1902,3805],[h_var,h_var]);
3、假设检验方法
检验序列是否存在单位根,存在为非平稳;不存在为平稳。
1)ADF检验
[h,pValue,stat,cValue]=adftest(pac_y)%h为1,数据平稳;h为0,数据不平稳。pValue越接近0越好
2)PP检验
[h_pp,pValue,stat,cValue]=pptest(pac_y)
3)KPSS检验
[h_kpss,pValue,stat,cValue]=kpsstest(pac_y)
二、白噪声分析
如果一个序列是白噪声,则无分析的意义,因为一个纯随机的数据提取不出任何有价值的规律。
BP检验和LB检验
BP检验
:无
LB检验
:
(74条消息) matlab5.白噪声检验_海滩超人的博客-CSDN博客_matlab白噪声序列检测
%白噪声检验
yanchi=[6,12,18]; %做6.12.18步延迟
[H,pValue,Qstat,CriticalValue]=lbqtest(pac_cf3pw,'lags',yanchi);
%lb检验 'lags'按照步长 延迟 ,x1改变就好了
%H,结果,p概率,Qlb的统计量,临界值
fprintf('%15s%15s%15s','延迟阶数','卡方统计量','p值');%把逗号后的字符串,15s的空格
fprintf('\n');
for i=1:length(yanchi) %i=1,时候为6,i=2时候为12
fprintf('%18f%19f%19f',yanchi(i),Qstat(i),pValue(i));
fprintf('\n');
end
%p比0.05大接受原假设,序列是个白噪声序列。
%原假设:一阶差分后序列延迟1.6.12步相关系数=0,一阶差分之后是一个白噪声序列
%既然白噪声序列就不能用时间序列了,一阶差分之后发现,内部没有存在相互传递的关系
三、时序模型建立
准备好时序数据

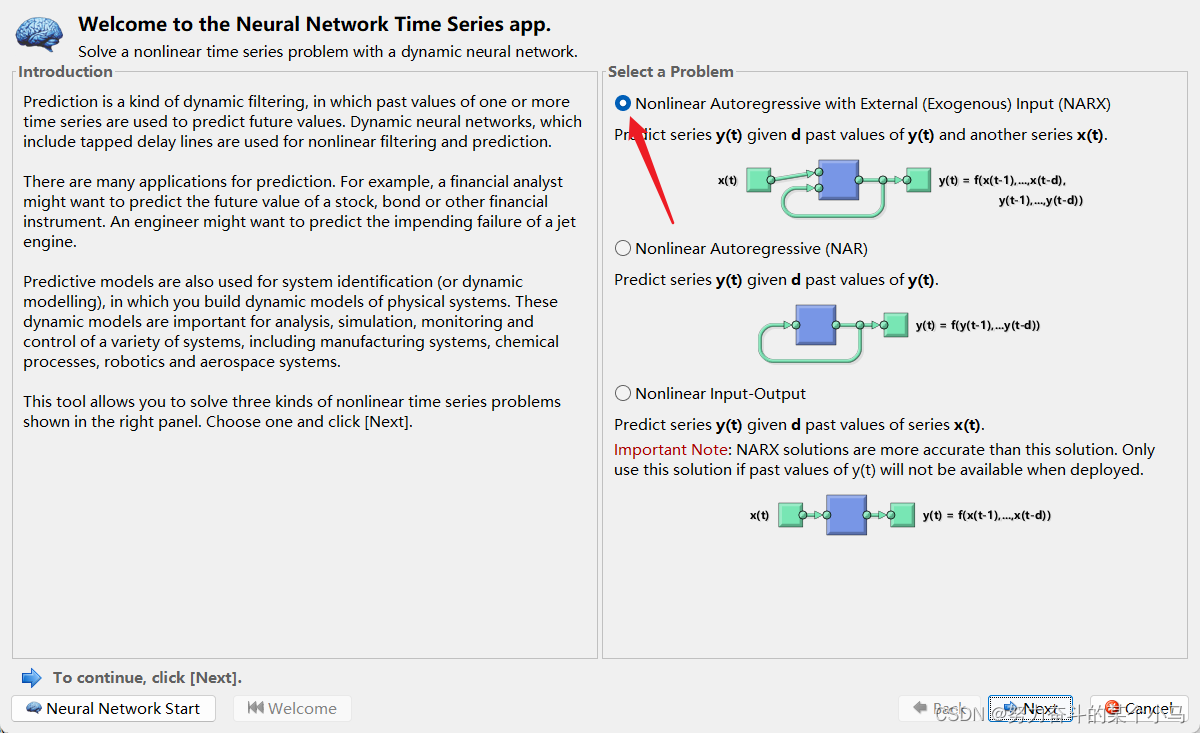
因为我有其他输入变量,所以选择了第一个。

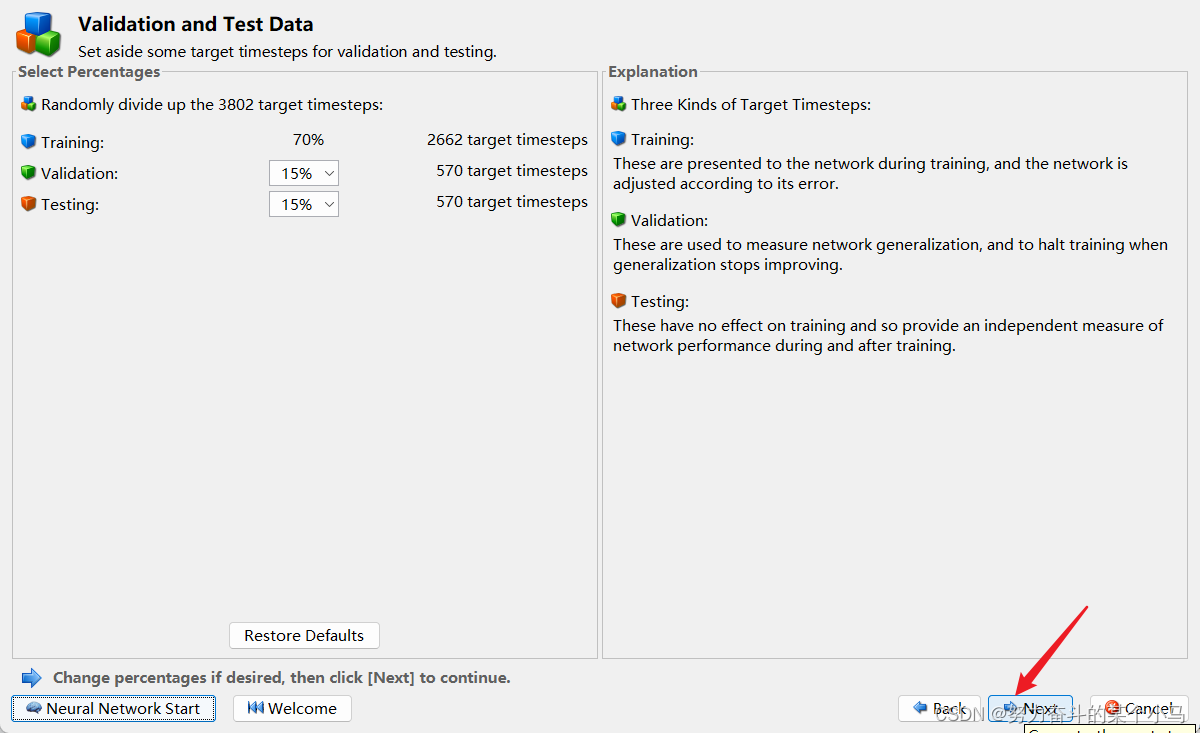
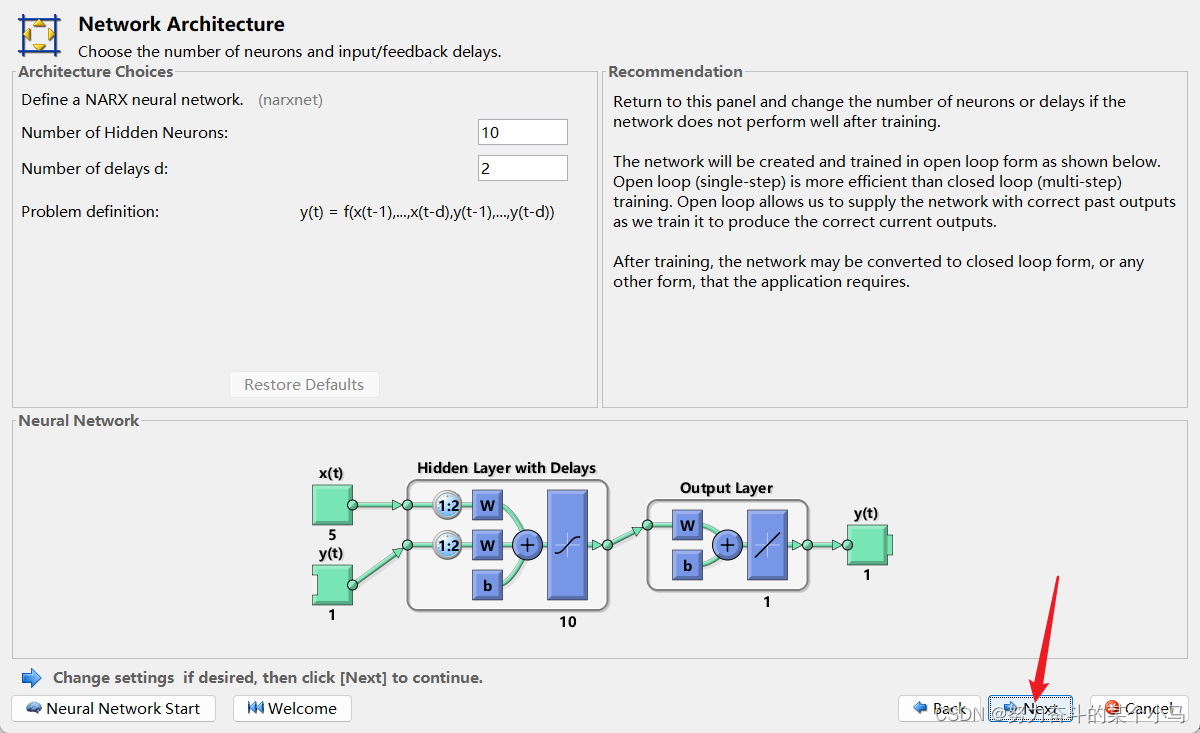

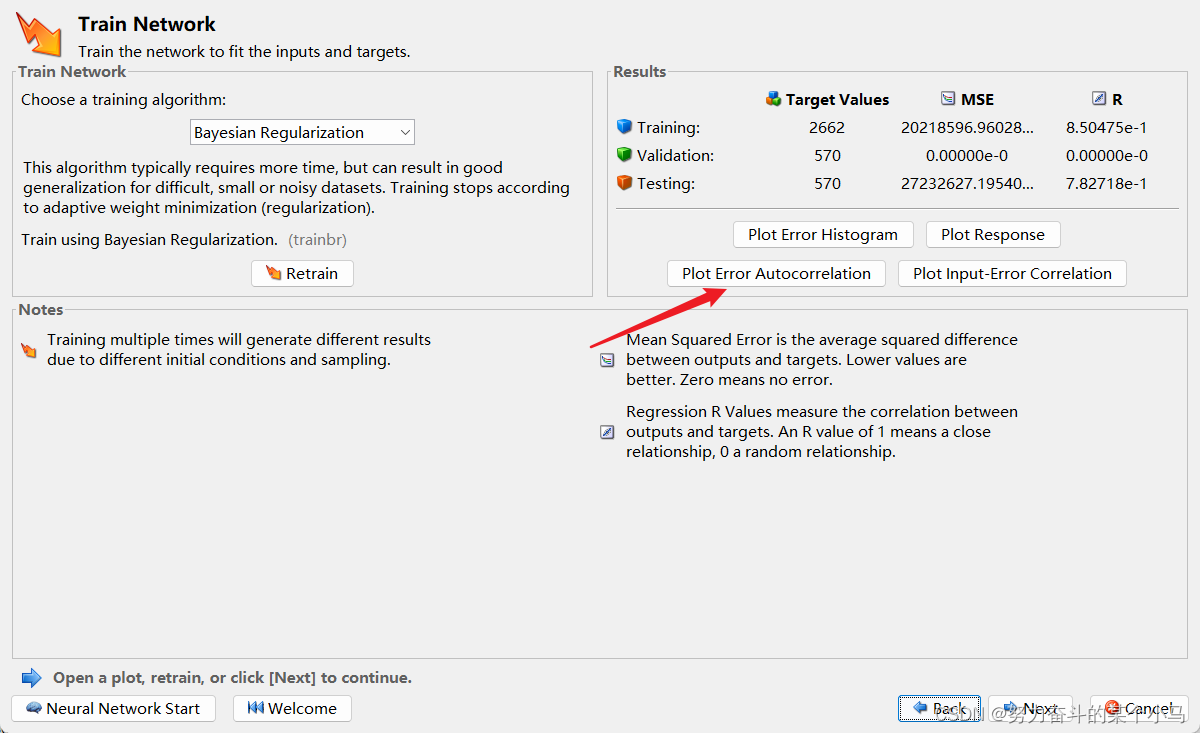
查看结果图。

四、结果分析