前言
做个编译器:
https://coolshell.cn/articles/1547.html
https://www.ctolib.com/docs/sfile/diy-c-compiler/1.html
BNF&递归
thrift的complier采用bison语法分析生成器来生成语法分析代码。bison通过编译thrifty.yy生成thrifty.h和thrifty.cc文件,这两个文件即是该compiler的语法分析代码。
概述
语法分析器使用词法分析器输出的token流作为输入,把token流转换成树状的中间表示,通常会转换成语法树,本文中使用的第一个例子比较简单,所以会对结果进行直接计算。复杂的语言通常会先构建语法树,然后在语法树的基础上做一系列的处理。如果输入的token流不符合语法分析器的规定的语法,语法分析器还可以报语法错误。语法树详解会在深入部分。
Bison的语法
Bison语法规则和Flex一样分为3个部分,第一部分是C语言声明、token声明、类型声明。由”%{“和”}%”围住的C语言部分会被直接拷贝到生成的语法分析器代码前面。第二部分是使用BNF语法编写的语法规则,为了编写方便,Bison对BNF做了一定的简化。第三部分是要执行的main函数。
下面是为集合运算语言AlphaGun编写的Bison规则,代码量比较大,可以直接翻到下面看解释
%{
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdarg.h>
#define NAME_SIZE 100
#define CHAR_SET_SIZE 26
extern int yylineno; /* from lexer */
int yylex();
void yyerror(char *s, ...)
{
va_list ap;
va_start(ap, s);
fprintf(stderr, "%d: error: ", yylineno);
vfprintf(stderr, s, ap);
fprintf(stderr, "\n");
}
struct Symbol
{
char name;
char value[CHAR_SET_SIZE];
};
struct Symbol symbol_table[26];
char temp_char_set[CHAR_SET_SIZE];
char factor_char_set[CHAR_SET_SIZE];
char expr_char_set[CHAR_SET_SIZE];
struct Symbol* NewSymbol()
{
struct Symbol* symbol = (struct Symbol*)malloc(sizeof(struct Symbol));
symbol->name = 0;
memset(symbol->value, 0, sizeof(symbol->value));
}
void PrintCharSet(char name, const char* char_set)
{
printf("%c: [", name);
int need_comma = 0;
for(int i=0; i< CHAR_SET_SIZE; i++)
{
if(char_set[i] != 0)
{
if(need_comma == 1)
{
printf(",");
}
printf("%c", char_set[i]);
need_comma = 1;
}
}
printf("]\n");
}
void PrintSymbol(const struct Symbol* symbol)
{
PrintCharSet(symbol->name, symbol->value);
}
void Union(char* result_char_set, const char* char_set_1, const char* char_set_2)
{
memcpy(result_char_set, char_set_1, CHAR_SET_SIZE);
for(int i=0; i<CHAR_SET_SIZE; i++)
{
if(char_set_2[i] != 0)
{
result_char_set[i] = char_set_2[i];
}
}
}
void Intersect(char* result_char_set, const char* char_set_1, const char* char_set_2)
{
for(int i=0;i <CHAR_SET_SIZE; i++)
{
if(char_set_1[i] != char_set_2[i] || char_set_1[i] == 0)
{
result_char_set[i] = 0;
}else
{
result_char_set[i] = char_set_1[i];
}
}
}
void Substract(char* result_char_set, const char* char_set_1, const char* char_set_2)
{
for(int i=0;i <CHAR_SET_SIZE; i++)
{
if(char_set_1[i] == 0 || char_set_1[i] == char_set_2[i])
{
result_char_set[i] = 0;
}else
{
result_char_set[i] = char_set_1[i];
}
}
}
%}
%union
{
char name;
char element;
char* char_set;
}
%token PRINT
%token <name> IDENTIFIER
%token <element> CHAR
%token COMMA
%token LEFT_BRACKET
%token RIGHT_BRACKET
%token ASSIGN
%token UNION
%token INTERSECT
%token SUBSTRACT
%token NEWLINE
%type <char_set> char_list init_list factor expr
%%
language: /* nothing */
| language statement NEWLINE
| language NEWLINE /*允许空行出现*/
statement: PRINT IDENTIFIER { PrintSymbol(&symbol_table[$2 - 'A']); }
| IDENTIFIER ASSIGN init_list { symbol_table[$1-'A'].name = $1; memcpy(symbol_table[$1-'A'].value, $3, CHAR_SET_SIZE); }
| IDENTIFIER ASSIGN expr { symbol_table[$1-'A'].name = $1; memcpy(symbol_table[$1-'A'].value, $3, CHAR_SET_SIZE); }
expr: factor { $$ = expr_char_set; memcpy($$, $1, CHAR_SET_SIZE); }
| expr SUBSTRACT factor { Substract($$, $1, $3); }
factor: IDENTIFIER { $$ = factor_char_set; memcpy($$, symbol_table[$1-'A'].value, CHAR_SET_SIZE); }
| factor UNION IDENTIFIER { Union($$, $1, symbol_table[$3-'A'].value); }
| factor INTERSECT IDENTIFIER { Intersect($$, $1, symbol_table[$3-'A'].value); }
init_list: LEFT_BRACKET char_list RIGHT_BRACKET { $$ = $2; }
char_list: CHAR { $$ = temp_char_set; memset($$, 0, 26); $$[$1-'a'] = $1; }
| char_list COMMA CHAR { $$[$3-'a'] = $3; }
%%
int main(int argc, char ** argv)
{
yyparse();
}
Bision规则第一部分
1、C语言部分:包含了需要的头文件,声明了几个函数,这些函数将在BNF语法规则部分用到。实现了yyerror,使得生成的语法分析器可以打印语法错误的相关信息,另外为了避免编译错误,前置声明了yylex。
2、token声明部分:首先定义了yylval的union类型。这里yylval由name、element、char_set三种变量联合组成,
%token IDENTIFIER
声明了IDENTIFIER token类型,并且告诉Bison,IDENTIFIER使用union类型的name变量存储值,这样在BNF语法规则部分,$ N就会直接指代name变量。类似的CHAR使用element变量,$N指代element。
3、type声明部分:声明了char_list, init_list, facotr, expr这4种非终结符使用union类型的char_set变量。如果没有这个声明的话,在BNF语法规则部分,是不能给非终结符的值变量$$赋值的。
Bison规则第二部分
第二部分是BNF语法规则部分,BNF语法规则如果细说的话又是一篇长文,这里简单介绍一下。每个规则的最左边是非终结符,冒号右边是非终结符的推导规则,一个非终结符如果有多个推导规则,使用竖线 | 分割。每个推导规则都可以对应一个动作,由 { } 包含,使用C语言代码编写。第一个规则的非终结符也被称为起始符,最终语言的全部输入都会最终匹配到起始符这里。Bison会自动对输入的token流进行解析,对匹配到的推导规则,执行动作代码,如果没有动作代码,会继续往下匹配。Bison中的每个token和非终结符都可以有一个值变量,这个是在上面的%token和%type声明中定义的。每个推导规则中,非终结符的值保存在
中,推导规则中出现的符号的值分别保存在$1、$2、$3、…中。
$$、$1、$2等实际指向的就是前面提到的yylval的union类型的具体变量。比如:
init_list: LEFT_BRACKET char_list RIGHT_BRACKET
init_list的值变量是$$,而LEFT_BRACKET的值变量就是$1,但是显然左括号不会有值,所以这里$1实际上是无用的,char_list的值变量是$2,在动作部分我们把$2赋值给了$1,从而实现了集合的初始化动作。
Bison规则第三部分
第三部分是main函数,直接调用了yyparse函数,yyparse是Bison生成的语法分析器入口,yyparse会不断地调用yylex获取token流去解析,和语法规则去做匹配,直到token流结束或者发现语法错误。
执行Bison
首先把
词法分析——lex/flex
中的Flex规则文件做一点修改,修改结果如下:
%option noyywrap yylineno
%{
#include <stdio.h>
#include "set_calc.tab.h"
int fileno(FILE *stream);
%}
%%
PRINT { return PRINT; }
[A-Z] { yylval.name = yytext[0]; return IDENTIFIER; }
[a-z] { yylval.element = yytext[0]; return CHAR; }
"," { return COMMA; }
"[" { return LEFT_BRACKET; }
"]" { return RIGHT_BRACKET; }
"=" { return ASSIGN; }
"∪" { return UNION; }
"∩" { return INTERSECT; }
"-" { return SUBSTRACT; }
\n { return NEWLINE; }
"//".* { /* omit comment*/ }
[ \t] { /*ignore white space*/ }
. { printf("unexpected token: (%s)\n", yytext); }
%%
删除了手动定义的枚举类型和yylva变量,包含了set_calc.tab.h头文件,这个头文件是由bison生成的,头文件中定义了枚举类型和yylval变量。为了避免编译错误,声明了fileno函数。
保存文件、联合Flex编译
把上面的Bison规则保存为set_calc.y,把flex规则保存为set_calc.l,编译
bison -d set_calc.y # 生成语法分析器
flex set_calc.l # 生成词法分析器
gcc -std=c99 -o set_calc set_calc.tab.c lex.yy.c # 编译生成可执行文件
编写AlphaGun语言代码,保存为test.set
A=[a,b,c,d,z]
B=[c,d,e, f ] // test comment
C=[e,f,g,h,z]
D=[x,y,z]
E = A ∪ B ∩ C - A ∩ B ∪ D
PRINT A
PRINT E
执行AlphaGun代码
./set_calc < test.set
运行结果
A: [a,b,c,d,z]
E: [e,f]
初步深入
我们看一下bison要做的工作,假如以以下lex文件分析出的内容为bison文件的输入:
%{
#include "stdio.h"
%}
%%
[\n] ; /*规则A*/
[0-9]+ printf("Int : %s\n",yytext); /*规则B*/
[0-9]*\.[0-9]+ printf("Float : %s\n",yytext); /*规则C*/
[a-zA-Z][a-zA-Z0-9]* printf("Var : %s\n",yytext); /*规则D*/
[/+/-/*///%] printf("Op : %s\n",yytext); /*规则E*/
. printf("Unknown : %c\n",yytext[0]); /*规则F*/
%%
file.txt文件:
i=1.344+39;
bcd=4%9-333
lex操作:
读入“i”
[查找元素]查找相邻且状态为1的元素,无元素,
[匹配规则]D,
[新增列表<元素1>并置数据] (存在则覆盖)状态为1,规则为D,内容为”i”。
[操作顺序符] 1
读入“=”
[查找元素]查找相邻且状态为1的元素,“i=”寻找匹配规则,无规则
[置上一元素]<元素1>状态为2
[匹配规则]F,
[新增列表<元素2>并置数据] (存在则覆盖)状态为1,规则为F,内容为”=”
[操作顺序符] 2
读入“1”,
[查找元素]查找相邻且状态为1的元素,“=1”寻找匹配规则,无规则
[置上一元素]<元素2>状态为2
[匹配规则]B,
[新增列表<元素3>并置数据] (存在则覆盖)状态为1,规则为B,内容为”1″
[操作顺序符] 3
读入“.”
[查找元素]查找相邻且状态为1的元素,“1.”寻找匹配规则,无规则,但有潜在规则C
[匹配规则]F,
[新增列表<元素4>并置数据] (存在则覆盖)状态为1,规则为F,内容为”.”
[置上一元素]<元素3>状态为1
[操作顺序符] 4
读入“3”
[查找元素]查找相邻且状态为1的元素,“1.3”寻找匹配规则,有规则
[置起始元素]状态为1,规则为C,内容为”1.3″
[操作顺序符] 3 组合元素的起始操作符
读入“4”
[查找元素]查找相邻且状态为1的元素,“1.34”寻找匹配规则,有规则
[置起始元素]状态为1,规则为C,内容为”1.34″
[操作顺序符] 3 组合元素的起始操作符
读入“4”
[查找元素]查找相邻且状态为1的元素,“1.344”寻找匹配规则,有规则
[置起始元素]状态为1,规则为C,内容为”1.344″
[操作顺序符] 3 组合元素的起始操作符
读入“+”
[查找元素]查找相邻且状态为1的元素,“1.344+”寻找匹配规则,无规则
[匹配规则]E,
[新增列表<元素4>并置数据] (存在则覆盖)状态为1,规则为E,内容为”+”
[置上一元素]<元素3>状态为2
[操作顺序符] 4
… …
lex最后解析结果为
| 内容 | 规则 | 状态 | |
|---|---|---|---|
| <元素1> | i | D | 2 |
| <元素2> | = | F | 2 |
| <元素3> | 1.344 | C | 2 |
| <元素4> | + | E | 2 |
yacc的BNF文件:
BNF能够用于表达上下文无关的语言。现代程序语言大多数结构能用BNF来描述。
例子:
1+2/3+4*6-3
BNF文法:
优先级
E = num 规约a 0
E = E / E 规约b 1
E = E * E 规约c 1
E = E + E 规约d 2
E = E - E 规约e 2
这里像(E表达式)这样出现在左边的结构叫做非终结符(nonterminal)。像(num标识符)这样的结构叫终结符(terminal,读了后面内容就会发现,其实是由lex返回的标记),它们只出现在右边。
我们将 “1+2/3+4*6-3-2”逐个字符移进堆栈,如下所示:
.1+2/3+4*6-3
1 1.+2/3+4*6-3 移进
2 E.+2/3+4*6-3 规约a
3 E+.2/3+4*6-3 移进
4 E+2./3+4*6-3 移进
5 E+E./3+4*6-3 规约a
6 E+E/.3+4*6-3 移进
7 E+E/3.+4*6-3 移进
8 E+E/E.+4*6-3 规约a
9 E+E/E+.4*6-3 移进
10 E+E/E+4.*6-3 移进
11 E+E/E+E.*6-3 规约a
12 E+E/E+E*.6-3 移进
13 E+E/E+E*6.-3 移进
14 E+E/E+E*E.-3 规约a
15 E+E/E+E*E-.3 移进
16 E+E/E+E*E-3. 移进
17 E+E/E+E*E-E. 规约a
18 E+E+E*E-E. 规约b
19 E+E+E-E. 规约c
20 E+E-E. 规约d
21 E-E. 规约d
22 E. 规约e
我们在实际运算操作中是把一个表达式逐步简化成一个非终结符。称之为“自底向上”或者“移进归约”的分析法。
点左面的结构在堆栈中,而点右面的是剩余的输入信息。我们以把标记移入堆栈开始。当堆栈顶部和右式要求的记号匹配时,我们就用左式取代所匹配的标记。概念上,匹配右式的标记被弹出堆栈,而左式被压入堆栈。我们把所匹配的标记认为是一个句柄,而我们所做的就是把句柄向左式归约。这个过程一直持续到把所有输入都压入堆栈中,而最终堆栈中只剩下最初的非终结符。
在第1步中我们把1压入堆栈中。第2步对应规则a,把1转换成E。然后继续压入和归约,直到第5步。此时堆栈中剩下E+E,按照规则d,可以进行E=E+E的合并,然而输入信息并没有结束,这就产生了
“移进-归约”冲突(shift-reduce conflict)
。在yacc中产生这种冲突时,会继续移进。
在第17步,E+E/E,即可以采用E+E规则d,也可以采用E/E规则b,如果使用E=E+E规约,显然从算法角度是错误的,这就有了运算符的优先级概念。这种情况称为
“归约-归约”冲突(reduce-reduce conflict)
。此时yacc会采用第一条规则,即E=E/E。
yacc的一个例子:
.l文件:
%{
#include <stdlib.h>
void yyerror(char *);
#include "lexya_a.tab.h" /*包含yacc生成的头文件*/
%}
%%
[0-9]+ { yylval = atoi(yytext); return INTEGER; }
[-+*/\n] return *yytext;
[\t] ;/* 去除空格 */
. yyerror("无效字符");
%%
int yywrap(void)
{
return 1;
}
.y文件
%{
#include <stdio.h>
int yylex(void);
void yyerror(char *);
%}
%token INTEGER /*%token INTEGER 定义声明了一个标记*/
%left '+' '-'
%left '*' '/'
%%
program:
program expr '\n'{printf("%d\n",$2);}
|
;
expr:
INTEGER{$$=$1;}
|expr '*' expr{$$=$1*$3;}
|expr '/' expr{$$=$1/$3;}
|expr '+' expr{$$=$1+$3;}
|expr '-' expr{$$=$1-$3;}
;
%%
void yyerror(char *s)
{
printf("%s\n",s);
}
int main()
{
yyparse();
return 0;
}
1、预定义标记部分:
%token INTEGER 定义声明了一个
标记
。
当我们编译后,它会在lexya_a.tab.c中生成一个
剖析器
,同时会在lexya_a.tab.h产生包含信息:
# define INTEGER 257
其中0-255的之间的标记值约定为字符值,是系统保留的后定义的token。
lexya_a.tab.h其它部分是默认生成的,与token INTEGER无关。
# ifndef YYSTYPE
# define YYSTYPE int
# define YYSTYPE_IS_TRIVIAL 1
# endif
extern YYSTYPE yylval;
lex文件需要包含这个头文件,并且使用其中对标记值的定义。
为了获得标记,yacc会调用yylex。yylex的返回值类型是整型,可以用于返回标记。而在yylval变量中保存着与返回的标记相对应的值。
yacc在内部维护着两个堆栈,一个
分析栈
和一个
内容栈
。分析栈中保存着终结符和非终结符,并且记录了当前剖析状态。而内容栈是一个YYSTYPE类型的元素数组,对于分析栈中的每一个元素都保存着一个对应的值。例如,当yylex返回一个INTEGER标记时,把这个标记移入分析栈。同时,相应的yacc值将会被移入内容栈中。分析栈和内容栈的内容总是同步的,因此从栈中找到对应的标记值是很容易的。
(很抽象,有时间还是得看看源码。)

比如lex文件中下面这一段:
[0-9]+ { yylval = atoi(yytext); return INTEGER; }
这是将把整数的值保存在yylval中,同时向yacc返回标记INTEGER。即内容栈存在了整数的值,对
应的分析栈就为INTEGER标记了。yylval类型由YYSTYPE决定,由于它的默认类型是整型,所以
在这个例子中程序运行正常。
lex文件还有一段:
[-+*/\n] return *yytext;
这里显然只是向yacc的分析栈返回运算符标记,系统保留的0-255此时便有了作用,内容栈为空。
把“-”放在第一位是防止正则表达式发现类似a-z的歧义。
%left '+' '-'
%left '*' '/'
%left 表示左结合,%right 表示右结合。最后列出的定义拥有最高的优先权。因此乘法和除法拥有
比加法和减法更高的优先权。+ - * / 所有这四个算术符都是左结合的。运用这个简单的技术,我们
可以消除文法的歧义。
注:关于结合性,各运算符的结合性分为两种,即左结合性(自左至右)和右结合性(自右至左)。例如算术运算符的结合性是自左至右,即先左后右。如有表达式x-y+z则y应先与“-”号结合, 执行x-y运算,然后再执行+z的运算。这种自左至右的结合方向就称为“左结合性”。而自右至左的结合方向称为“右结合性”。 最典型的右结合性运算符是赋值运算符。如x=y=z,由于“=”的右结合性,应先执行y=z再执行x=(y=z)运算。
2、规则部分:
先看expr,可以由单个INTEGER值组成,也可以有多个INTERGER和运算符组合组成。
以表达式
1+4/2*3-0
为例,1 4 2 3 都是expr,就是expr+expr/expr*expr-expr
说到底最后还是个expr。递归思想正好与之相反,逆推下去会发现expr这个规则标记能表示所有的数值运算表达式。
了解了expr后,再看program,首先program可以为空,也可以用单单的expr加下“/n”回车符组成,结合起来看program定义的就是多个表达式组成的文件内容。
粗略有了概念后,再看看lex如何执行相应的行为:
以expr:expr '+'expr{$$= $1 + $3; }为例: 在分析栈中我们其实用左式替代了右式。在本例中,我
们弹出“ expr '+' expr ” 然后压入“expr”。我们通过弹出三个成员,压入一个成员来缩小堆栈。在我们
的代码中 可以看到用相对地址访问内容栈中的值。如$1,$2,这样都是yacc预定义可以直接使用的
标记。“$1”代表右式中的第一个成员,“$2”代表第二个,后面的以此类推。“
而program:
program expr '/n' { printf("%d/n", $2); }
说明每当一行表达式结束时,打印出第二个栈值,即expr的值,完成字符运算。
然后现在数据就在分析栈和内容栈中,接下来yacc怎么对其中的内容进行解析呢?
yyparse
语法树
一、导言

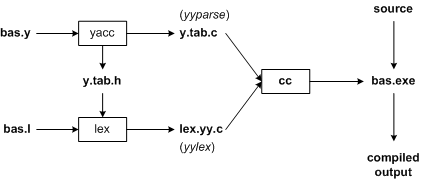
网上找的图,比我画的更清晰明了。
x = 0;
while (x < 3) {
print x;
x = x + 1;
}
解释版本的输出数据:
0
1
2
编译版本的输出数据:
push 0
pop x
L000:
push x
push 3
compLT
jz L001
push x
print
push x
push 1
add
pop x
jmp L000
L001:
生成语法树的版本输出:
[=]
|
|----|
| |
id(X) c(0)
Graph 1:
while
|
|----------------|
| |
[<] [;]
| |
|----| |----------|
| | | |
id(X) c(3) print [=]
| |
| |-------|
| | |
id(X) id(X) [+]
|
|----|
| |
id(X) c(1)
包含文件中包括了对语法树和符号表的定义。符号表 sym 允许使用单个字符表示变量名。语法 树中的每个节点保存一个常量(conNodeType)、标识符(idNodeType)、或者一个带算子 (oprNodeType)的内部节点。所有这三种变量压缩在一个 union 结构中,而节点的具体类型跟据 其内部所拥有的结构来判断。
lex 输入文件中包含有返回 VARIABLE 和 INTEGER 标志的正则表达式。另外,也定义了像 EQ 和 NE 这样的双字符算子的标志。对于单字符算子,只需简单地返回其本身。
yacc 输入文件中定义了 YYSTYPE,yylval 的类型,定义如下
%union {
int iValue; /* integer value */
char sIndex; /* symbol table index */
nodeType *nPtr; /* node pointer */
};
这将导致在 y.tab.h 中生成如下代码:
typedef union {
int iValue; /* integer value */
char sIndex; /* symbol table index */
nodeType *nPtr; /* node pointer */
} YYSTYPE;
extern YYSTYPE yylval;
在剖析器的内容栈中,常量、变量和节点都可以由 yylval 表示。
0 {
yylval.iValue = atoi(yytext);
return INTEGER;
}
[1-9][0-9]* {
yylval.iValue = atoi(yytext);
return INTEGER;
}
注意下面的定义:
%token <iValue> INTEGER
%type <nPtr> expr
这把 expr 和 INTEGER 分别绑定到 union 结构 YYSTYPE 中的 nPtr 和 iValue 成员。这是必须的,只有这样 yacc 才能生成正确的代码。例如,这个规则:
expr: INTEGER { $$ = con($1); }
可以生成下面的代码。注意,yyvsp[0] 表示内容栈的顶部,或者表示对应于 INTEGER 的值。
yylval.nPtr = con(yyvsp[0].iValue);
一元算子的优先级比二元算子要高,如下所示:
%left GE LE EQ NE '>' '<'
%left '+' '-'
%left '*' '/'
%nonassoc UMINUS
%nonassoc 意味着没有依赖关系。它经常在连接词中和 %prec 一起使用,用于指定一个规则的 优先级。因此,我们可以这样:
expr: '' expr %prec UMINUS { $$ = node(UMINUS, 1, $2); }
表示这条规则的优先级和标志 UMINUS 相同。而且,如同上面所定义的,UMINUS 的优先级比其 它所有算子都高。类似的技术也用于消除 ifelse 结构中的二义性(请看 ifelse 二义性)。
语法树是从底向上构造的,当变量和整数减少时才分配叶节点。当遇到算子时,就需要分配一 个节点,并且把上一个分配的节点作为操作数记录在其中。
构造完语法树之后,调用函数 ex 对此语法树进行第一深度历遍。第一深度历遍按照原先节点 分配的顺序访问各节点。
这将导致各算子按照剖析期间的访问顺序被使用。此处含有三个版本的 ex 函数:一个解释版 本,一个编译版本,一个用于生成语法树的版本。
包含文件
typedef enum { typeCon, typeId, typeOpr } nodeEnum;
/* constants */
typedef struct {
int value; /* value of constant */
} conNodeType;
/* identifiers */
typedef struct {
int i; /* subscript to sym array */
} idNodeType;
/* operators */
typedef struct {
int oper; /* operator */
int nops; /* number of operands */
struct nodeTypeTag *op[1]; /* operands, extended at runtime */
} oprNodeType;
typedef struct nodeTypeTag {
nodeEnum type; /* type of node */
union {
conNodeType con; /* constants */
idNodeType id; /* identifiers */
oprNodeType opr; /* operators */
};
} nodeType;
extern int sym[26];
Lex 输入文件
%{
#include <stdlib.h>
#include "calc3.h"
#include "y.tab.h"
void yyerror(char *);
%}
%%
[a-z] {
yylval.sIndex = *yytext - 'a';
return VARIABLE;
}
0 {
yylval.iValue = atoi(yytext);
return INTEGER;
}
[1-9][0-9]* {
yylval.iValue = atoi(yytext);
return INTEGER;
}
[-()<>=+*/;{}.] {
return *yytext;
}
">=" return GE;
"<=" return LE;
"==" return EQ;
"!=" return NE;
"while" return WHILE;
"if" return IF;
"else" return ELSE;
"print" return PRINT;
[ \t\n]+ ; /* ignore whitespace */
. yyerror("Unknown character");
%%
int yywrap(void) {
return 1;
}
Yacc 输入文件
%{
#include <stdio.h>
#include <stdlib.h>
#include <stdarg.h>
#include "calc3.h"
/* prototypes */
nodeType *opr(int oper, int nops, ...);
nodeType *id(int i);
nodeType *con(int value);
void freeNode(nodeType *p);
int ex(nodeType *p);
int yylex(void);
void yyerror(char *s);
int sym[26]; /* symbol table */
%}
%union {
int iValue; /* integer value */
char sIndex; /* symbol table index */
nodeType *nPtr; /* node pointer */
};
%token <iValue> INTEGER
%token <sIndex> VARIABLE
%token WHILE IF PRINT
%nonassoc IFX
%nonassoc ELSE
%left GE LE EQ NE '>' '<'
%left '+' '-'
%left '*' '/'
%nonassoc UMINUS
%type <nPtr> stmt expr stmt_list
%%
program:
function { exit(0); }
;
function:
function stmt { ex($2); freeNode($2); }
| /* NULL */
;
stmt:
';' { $$ = opr(';', 2, NULL, NULL); }
| expr ';' { $$ = $1; }
| PRINT expr ';' { $$ = opr(PRINT, 1, $2); }
| VARIABLE '=' expr ';' { $$ = opr('=', 2, id($1), $3); }
| WHILE '(' expr ')' stmt { $$ = opr(WHILE, 2, $3, $5); }
| IF '(' expr ')' stmt %prec IFX { $$ = opr(IF, 2, $3, $5); }
| IF '(' expr ')' stmt ELSE stmt { $$ = opr(IF, 3, $3, $5, $7); }
| '{' stmt_list '}' { $$ = $2; }
;
stmt_list:
stmt { $$ = $1; }
| stmt_list stmt { $$ = opr(';', 2, $1, $2); }
;
expr:
INTEGER { $$ = con($1); }
| VARIABLE { $$ = id($1); }
| '-' expr %prec UMINUS { $$ = opr(UMINUS, 1, $2); }
| expr '+' expr { $$ = opr('+', 2, $1, $3); }
| expr '-' expr { $$ = opr('-', 2, $1, $3); }
| expr '*' expr { $$ = opr('*', 2, $1, $3); }
| expr '/' expr { $$ = opr('/', 2, $1, $3); }
| expr '<' expr { $$ = opr('<', 2, $1, $3); }
| expr '>' expr { $$ = opr('>', 2, $1, $3); }
| expr GE expr { $$ = opr(GE, 2, $1, $3); }
| expr LE expr { $$ = opr(LE, 2, $1, $3); }
| expr NE expr { $$ = opr(NE, 2, $1, $3); }
| expr EQ expr { $$ = opr(EQ, 2, $1, $3); }
| '(' expr ')' { $$ = $2; }
;
%%
nodeType *con(int value) {
nodeType *p;
/* allocate node */
if ((p = malloc(sizeof(nodeType))) == NULL)
yyerror("out of memory");
/* copy information */
p->type = typeCon;
p->con.value = value;
return p;
}
nodeType *id(int i) {
nodeType *p;
/* allocate node */
if ((p = malloc(sizeof(nodeType))) == NULL)
yyerror("out of memory");
/* copy information */
p->type = typeId;
p->id.i = i;
return p;
}
nodeType *opr(int oper, int nops, ...) {
va_list ap;
nodeType *p;
int i;
/* allocate node, extending op array */
if ((p = malloc(sizeof(nodeType) + (nops-1) * sizeof(nodeType *))) == NULL)
yyerror("out of memory");
/* copy information */
p->type = typeOpr;
p->opr.oper = oper;
p->opr.nops = nops;
va_start(ap, nops);
for (i = 0; i < nops; i++)
p->opr.op[i] = va_arg(ap, nodeType*);
va_end(ap);
return p;
}
void freeNode(nodeType *p) {
int i;
if (!p) return;
if (p->type == typeOpr) {
for (i = 0; i < p->opr.nops; i++)
freeNode(p->opr.op[i]);
}
free (p);
}
void yyerror(char *s) {
fprintf(stdout, "%s\n", s);
}
int main(void) {
yyparse();
return 0;
}
解释器版本
#include <stdio.h>
#include "calc3.h"
#include "y.tab.h"
int ex(nodeType *p) {
if (!p) return 0;
switch(p->type) {
case typeCon: return p->con.value;
case typeId: return sym[p->id.i];
case typeOpr:
switch(p->opr.oper) {
case WHILE: while(ex(p->opr.op[0])) ex(p->opr.op[1]); return 0;
case IF: if (ex(p->opr.op[0]))
ex(p->opr.op[1]);
else if (p->opr.nops > 2)
ex(p->opr.op[2]);
return 0;
case PRINT: printf("%d\n", ex(p->opr.op[0])); return 0;
case ';': ex(p->opr.op[0]); return ex(p->opr.op[1]);
case '=': return sym[p->opr.op[0]->id.i] = ex(p->opr.op[1]);
case UMINUS: return -ex(p->opr.op[0]);
case '+': return ex(p->opr.op[0]) + ex(p->opr.op[1]);
case '-': return ex(p->opr.op[0]) - ex(p->opr.op[1]);
case '*': return ex(p->opr.op[0]) * ex(p->opr.op[1]);
case '/': return ex(p->opr.op[0]) / ex(p->opr.op[1]);
case '<': return ex(p->opr.op[0]) < ex(p->opr.op[1]);
case '>': return ex(p->opr.op[0]) > ex(p->opr.op[1]);
case GE: return ex(p->opr.op[0]) >= ex(p->opr.op[1]);
case LE: return ex(p->opr.op[0]) <= ex(p->opr.op[1]);
case NE: return ex(p->opr.op[0]) != ex(p->opr.op[1]);
case EQ: return ex(p->opr.op[0]) == ex(p->opr.op[1]);
}
}
return 0;
}
编译器版本
#include <stdio.h>
#include "calc3.h"
#include "y.tab.h"
static int lbl;
int ex(nodeType *p) {
int lbl1, lbl2;
if (!p) return 0;
switch(p->type) {
case typeCon:
printf("\tpush\t%d\n", p->con.value);
break;
case typeId:
printf("\tpush\t%c\n", p->id.i + 'a');
break;
case typeOpr:
switch(p->opr.oper) {
case WHILE:
printf("L%03d:\n", lbl1 = lbl++);
ex(p->opr.op[0]);
printf("\tjz\tL%03d\n", lbl2 = lbl++);
ex(p->opr.op[1]);
printf("\tjmp\tL%03d\n", lbl1);
printf("L%03d:\n", lbl2);
break;
case IF:
ex(p->opr.op[0]);
if (p->opr.nops > 2) {
/* if else */
printf("\tjz\tL%03d\n", lbl1 = lbl++);
ex(p->opr.op[1]);
printf("\tjmp\tL%03d\n", lbl2 = lbl++);
printf("L%03d:\n", lbl1);
ex(p->opr.op[2]);
printf("L%03d:\n", lbl2);
} else {
/* if */
printf("\tjz\tL%03d\n", lbl1 = lbl++);
ex(p->opr.op[1]);
printf("L%03d:\n", lbl1);
}
break;
case PRINT:
ex(p->opr.op[0]);
printf("\tprint\n");
break;
case '=':
ex(p->opr.op[1]);
printf("\tpop\t%c\n", p->opr.op[0]->id.i + 'a');
break;
case UMINUS:
ex(p->opr.op[0]);
printf("\tneg\n");
break;
default:
ex(p->opr.op[0]);
ex(p->opr.op[1]);
switch(p->opr.oper) {
case '+': printf("\tadd\n"); break;
case '-': printf("\tsub\n"); break;
case '*': printf("\tmul\n"); break;
case '/': printf("\tdiv\n"); break;
case '<': printf("\tcompLT\n"); break;
case '>': printf("\tcompGT\n"); break;
case GE: printf("\tcompGE\n"); break;
case LE: printf("\tcompLE\n"); break;
case NE: printf("\tcompNE\n"); break;
case EQ: printf("\tcompEQ\n"); break;
}
}
}
return 0;
}
AST抽象语法树版本
/* source code courtesy of Frank Thomas Braun */
/* Generation of the graph of the syntax tree */
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include "calc3.h"
#include "y.tab.h"
int del = 1; /* distance of graph columns */
int eps = 3; /* distance of graph lines */
/* interface for drawing (can be replaced by "real" graphic using GD or other) */
void graphInit (void);
void graphFinish();
void graphBox (char *s, int *w, int *h);
void graphDrawBox (char *s, int c, int l);
void graphDrawArrow (int c1, int l1, int c2, int l2);
/* recursive drawing of the syntax tree */
void exNode (nodeType *p, int c, int l, int *ce, int *cm);
/*****************************************************************************/
/* main entry point of the manipulation of the syntax tree */
int ex (nodeType *p) {
int rte, rtm;
graphInit ();
exNode (p, 0, 0, &rte, &rtm);
graphFinish();
return 0;
}
/*c----cm---ce----> drawing of leaf-nodes
l leaf-info
*/
/*c---------------cm--------------ce----> drawing of non-leaf-nodes
l node-info
* |
* ------------- ...----
* | | |
* v v v
* child1 child2 ... child-n
* che che che
*cs cs cs cs
*
*/
void exNode
( nodeType *p,
int c, int l, /* start column and line of node */
int *ce, int *cm /* resulting end column and mid of node */
)
{
int w, h; /* node width and height */
char *s; /* node text */
int cbar; /* "real" start column of node (centred above subnodes) */
int k; /* child number */
int che, chm; /* end column and mid of children */
int cs; /* start column of children */
char word[20]; /* extended node text */
if (!p) return;
strcpy (word, "???"); /* should never appear */
s = word;
switch(p->type) {
case typeCon: sprintf (word, "c(%d)", p->con.value); break;
case typeId: sprintf (word, "id(%c)", p->id.i + 'A'); break;
case typeOpr:
switch(p->opr.oper){
case WHILE: s = "while"; break;
case IF: s = "if"; break;
case PRINT: s = "print"; break;
case ';': s = "[;]"; break;
case '=': s = "[=]"; break;
case UMINUS: s = "[_]"; break;
case '+': s = "[+]"; break;
case '-': s = "[-]"; break;
case '*': s = "[*]"; break;
case '/': s = "[/]"; break;
case '<': s = "[<]"; break;
case '>': s = "[>]"; break;
case GE: s = "[>=]"; break;
case LE: s = "[<=]"; break;
case NE: s = "[!=]"; break;
case EQ: s = "[==]"; break;
}
break;
}
/* construct node text box */
graphBox (s, &w, &h);
cbar = c;
*ce = c + w;
*cm = c + w / 2;
/* node is leaf */
if (p->type == typeCon || p->type == typeId || p->opr.nops == 0) {
graphDrawBox (s, cbar, l);
return;
}
/* node has children */
cs = c;
for (k = 0; k < p->opr.nops; k++) {
exNode (p->opr.op[k], cs, l+h+eps, &che, &chm);
cs = che;
}
/* total node width */
if (w < che - c) {
cbar += (che - c - w) / 2;
*ce = che;
*cm = (c + che) / 2;
}
/* draw node */
graphDrawBox (s, cbar, l);
/* draw arrows (not optimal: children are drawn a second time) */
cs = c;
for (k = 0; k < p->opr.nops; k++) {
exNode (p->opr.op[k], cs, l+h+eps, &che, &chm);
graphDrawArrow (*cm, l+h, chm, l+h+eps-1);
cs = che;
}
}
/* interface for drawing */
#define lmax 200
#define cmax 200
char graph[lmax][cmax]; /* array for ASCII-Graphic */
int graphNumber = 0;
void graphTest (int l, int c)
{ int ok;
ok = 1;
if (l < 0) ok = 0;
if (l >= lmax) ok = 0;
if (c < 0) ok = 0;
if (c >= cmax) ok = 0;
if (ok) return;
printf ("\n+++error: l=%d, c=%d not in drawing rectangle 0, 0 ... %d, %d",
l, c, lmax, cmax);
exit(1);
}
void graphInit (void) {
int i, j;
for (i = 0; i < lmax; i++) {
for (j = 0; j < cmax; j++) {
graph[i][j] = ' ';
}
}
}
void graphFinish() {
int i, j;
for (i = 0; i < lmax; i++) {
for (j = cmax-1; j > 0 && graph[i][j] == ' '; j--);
graph[i][cmax-1] = 0;
if (j < cmax-1) graph[i][j+1] = 0;
if (graph[i][j] == ' ') graph[i][j] = 0;
}
for (i = lmax-1; i > 0 && graph[i][0] == 0; i--);
printf ("\n\nGraph %d:\n", graphNumber++);
for (j = 0; j <= i; j++) printf ("\n%s", graph[j]);
printf("\n");
}
void graphBox (char *s, int *w, int *h) {
*w = strlen (s) + del;
*h = 1;
}
void graphDrawBox (char *s, int c, int l) {
int i;
graphTest (l, c+strlen(s)-1+del);
for (i = 0; i < strlen (s); i++) {
graph[l][c+i+del] = s[i];
}
}
void graphDrawArrow (int c1, int l1, int c2, int l2) {
int m;
graphTest (l1, c1);
graphTest (l2, c2);
m = (l1 + l2) / 2;
while (l1 != m) { graph[l1][c1] = '|'; if (l1 < l2) l1++; else l1--; }
while (c1 != c2) { graph[l1][c1] = '-'; if (c1 < c2) c1++; else c1--; }
while (l1 != l2) { graph[l1][c1] = '|'; if (l1 < l2) l1++; else l1--; }
graph[l1][c1] = '|';
}
二、递归的一些思想
我们先看一个简化的C语言示例段:
i=0;
while(i<=10) {
print(i);
i=i+1;
}
print(i+i);
首先,我们将()+/* print while之类的组合称为expr(expression),仅表示基本的表达式,可
以理解通过递归可以进行任意的运算符组合。如下面每一行都可称为expr:
i=0
while(i<=10)
print(i)
i=i+1
print(i+i)
再把expr + ;的语句行称为stmt(statement),表示一条语句的结束。把{}引起来的多个stmt
称为stmt_list。如此,原示例段可表示为:
stmt
expr stmt_list
stmt
这样显然不符合递归法则,倘若stmt也可由expr stmt_list组合,程序则可以递归到最顶级
stmt
stmt
stmt
这也要求yacc文法定义必须可以递归到最顶级,即如上所示。
BNF&递归部分看文章:
https://blog.csdn.net/weixin_44705391/article/details/116190795?spm=1001.2014.3001.5501
高级yylval: union
YACC的yylval类型是取决于YYSTYPE。如果yylval是个联合体,它即可以处理字符串,也可以是整数,但不是同时处理这两种。我们可以通过定义YYSTYPE为联合体。不过YACC有一个更简单的方法:使用%union语句。
%union {
int number;
char *string;
}
%token STATE
%token NUMBER
%token WORD
定义了我们的联合体,它仅包含数字和字体串,然后使用一个扩展的%token语法,告诉YACC应该取联合体的哪一个部分。
我们不再直接获取yylval的值,而是添加一个后缀指示想取得哪个部分的值。
%{
#include <stdio.h>
#include <string.h>
#include “y.tab.h”
%}
%%
[0−9]+ yylval.number=atoi(yytext); return NUMBER;
[a-z][a−z0−9]+ yylval.string=yytext; return WORD;
%%
不过在YACC语法中,我们无须这样做,因为YACC为我们做了神奇的这些, 由于上面的%token定义,YACC自动从联合体中挑选string成员。
heater_select:
TOKHEATER WORD {
printf(“Selected heater ‘%s’\n”, $2);
heater = $2;
}
;
需要注意的是,一般来时,yyvsp[0]相当于$1, yyvsp[1]相当于$2,但是,在当yylval为union的时候,$1相当于yysvp[0]的某个类型的值,这个类型是Yacc推断出来的类型。例如,上例中的$2相当于yyvsp[1].string。因此,使用%union的时候的尤其注意这个问题。我们知道,在C语言中,Union在bit级别上是低位对齐(所有成员都从低地址开始存放的)的,因此,有些时候这可能会导致某些错误。
Inter X86 CPU是小端(Little-endian)模式, 例如,0x12345678在内存中的排列情况为:
内存地址 存放内容
0x4000 0x78
0x4001 0x56
0x4002 0x34
0x4003 0x12
因此,在使用Yacc时,对于由于类型判断错误而导致的union的值错误的情形要非常谨慎。
有歧义的文法
通常文法是有歧义的,比如:四则运算”34+5“,应该如何分组操作符?这个表达式的意思是(34)+5,还是3*(4+5)?当yacc遇到歧义的文法时,会报错”shift/reduce”冲突或者”reduce/reduce”冲突。
遇到”shift/reduce”冲突是因为yacc在遇到一个词法单元时,不知道应该执行规约动作还是执行词法单元移动。
出现”shift/reduce”冲突时,yacc可以根据规则的优先级和结合性进行处理,具体规则:
如果当前的词法单元的优先级高于解析栈中规则,那么执行shift动作。
如果当前的词法单元的优先级低于解析栈中规则,那么将栈中的规则进行规约。
在当前的词法单元和解析栈中规则的优先级相同的情况下,如果规则是左结合性,那么执行规约动作,否则执行shift。
如果没有提供优先级和结合性,那么默认执行shift动作。
StackOverflow上有一个问题是一个很好的处理”shift/reduce conflicts”的例子:Shift/reduce conflicts in bison
“reduce/reduce”冲突就是解析栈中可以应用多个规则进行规约,这种冲突的解决就是选择第一个出现的规则进行规约。一般出现这种冲突主要是因为不同的规则集合可以产生相同的词法单元序列。
通过%nonassoc指定操作符不具备结合性。nonassoc, 意味着没有依赖关系。它经常在连接词中和 %prec一起使用,用于指定一个规则的优先级。
以If-Else的冲突为例,当有两个IF一个ELSE时,该ELSE和哪个IF匹配是一个问题。有两中匹配方法:与第一个匹配和与第二匹配。现代程序语言都让ELSE与最近的IF匹配,这也是yacc的缺省行为。虽然yacc行为正确,但为避免警告,可以给IF-ELSE语句比IF语句更高的优先级:
%nonassoc IFX
%nonassoc ELSE
stmt:
IF expr stmt %prec IFX
| IF expr stmt ELSE stmt
一个关于’%prec’的解释:
It declares that that construct has the same precedence as the ‘.’ operator, which will have been specified earlier.
参考文章:
https://blog.csdn.net/damontive/article/details/115289918
https://blog.csdn.net/liwei_cmg/article/details/1530999
https://blog.csdn.net/liwei_cmg/article/details/1618822
https://my.oschina.net/fileoptions/blog/1647222