博客

C. Covered Points Count

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given
$\mathrm{n\; n segments\; on\; a\; coordinate\; line;\; each\; endpoint\; of\; every\; segment\; has\; integer\; coordinates.\; Some\; segments\; can\; degenerate\; to\; points.\; Segments\; can\; intersect\; with\; each\; other,\; be\; nested\; in\; each\; other\; or\; even\; coincide.}$

Your task is the following: for every
$\mathrm{k\; \in \; [\; 1..\; n\; ]\; k\in [1..n],\; calculate\; the\; number\; of\; points\; with\; integer\; coordinates\; such\; that\; the\; number\; of\; segments\; that\; cover\; these\; points\; equals\; k\; k.\; A\; segment\; with\; endpoints\; l\; i\; li and\; r\; i\; ri covers\; point\; x\; x if\; and\; only\; if\; l\; i\; \le \; x\; \le \; r\; i\; li\le x\le ri.}$

Input

The first line of the input contains one integer
$\mathrm{n\; n (\; 1\; \le \; n\; \le \; 2\; \cdot \; 10\; 5\; 1\le n\le 2\cdot 105)\; —\; the\; number\; of\; segments.}$

The next
$\mathrm{n\; n lines\; contain\; segments.\; The\; i\; i-th\; line\; contains\; a\; pair\; of\; integers\; l\; i\; ,\; r\; i\; li,ri (\; 0\; \le \; l\; i\; \le \; r\; i\; \le \; 10\; 18\; 0\le li\le ri\le 1018)\; —\; the\; endpoints\; of\; the\; i\; i-th\; segment.}$

Output

Print
$\mathrm{n\; n space\; separated\; integers\; c\; n\; t\; 1\; ,\; c\; n\; t\; 2\; ,\; \dots \; ,\; c\; n\; t\; n\; cnt1,cnt2,\dots ,cntn,\; where\; c\; n\; t\; i\; cnti is\; equal\; to\; the\; number\; of\; points\; such\; that\; the\; number\; of\; segments\; that\; cover\; these\; points\; equals\; to\; i\; i.}$

Examples

input

Copy

3
0 3
1 3
3 8

output

Copy

6 2 1 

input

Copy

3
1 3
2 4
5 7

output

Copy

5 2 0 

Note

The picture describing the first example:

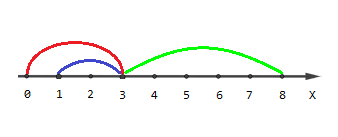
Points with coordinates
$[\; 0\; ,\; 4\; ,\; 5\; ,\; 6\; ,\; 7\; ,\; 8\; ]\; [0,4,5,6,7,8] are\; covered\; by\; one\; segment,\; points\; [\; 1\; ,\; 2\; ]\; [1,2] are\; covered\; by\; two\; segments\; and\; point\; [\; 3\; ]\; [3] is\; covered\; by\; three\; segments.$

The picture describing the second example:

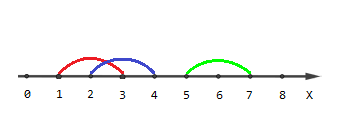
Points
$[\; 1\; ,\; 4\; ,\; 5\; ,\; 6\; ,\; 7\; ]\; [1,4,5,6,7] are\; covered\; by\; one\; segment,\; points\; [\; 2\; ,\; 3\; ]\; [2,3] are\; covered\; by\; two\; segments\; and\; there\; are\; no\; points\; covered\; by\; three\; segments.$

这题坑点比较多，没有开LLwa一发 ，数组开小了又wa一发 难受

细节方面很多都没有注意到

这题是纯思维题 把每一个区间分为两个点一个左端点一个右端点

进行排序一下，就出来了

从左往右扫一遍经历一次左端点就加一，经历一次又端点就减一

这个规律看图一下就出来了

#include <bits/stdc++.h>
using namespace std;
const int maxn = 4e5 + 10;
typedef long long LL;
struct node {
    LL x, y;
    node (LL x, LL y) : x(x), y(y) {}
    node () {}
} qu[maxn];
int cmp(node a, node b) {
    if (a.x == b.x) return a.y > b.y;
    return a.x < b.x;
}
LL ans[maxn];
int main() {
    LL n,k=0,a,b;
    scanf("%lld", &n);
    for (int i = 0 ; i < n ; i++) {
        scanf("%lld%lld",&a,&b);
        qu[k++] = node(a, 1);
        qu[k++] = node(b + 1, -1);
    }
    sort(qu, qu + k, cmp);
    LL temp = 0;
    for(int i = 0 ; i < k-1  ; i++ ) {
        temp += qu[i].y;
        if (qu[i].x != qu[i + 1].x) ans[temp]+= qu[i + 1].x - qu[i].x;
    }
    for (int i = 1 ; i <=n ; i++)
        printf("%lld ", ans[i]);
    printf("\n");
    return 0;
}